propofée à ce cas qu’il faut s’appliquer. Soit donc
A y '+ B qui doit êtreun quarré A , & B n ayant point
de fafteurs quarrés ; car s’ils en avoient, il n y aurait
qu’à divifer A ôc i? par les'fafteurs 6t refoudre
la queftion — b j t égal à un quarré » &
faire y =-— •
Je fais y — E, p & ? étant des nombres entiers
premiers entr’eux A ^7 •+- B fera donc un quatre,
& l’équation A p2 + Bq * = <2 a fera réfoluble en
nombres entiers. De ce que/> & * font premiers
entr’eu x, p & B le feront aufli ; autrement il faudra
que le divifeur tB q* fut divifible par r2 & 5
ne l’étant que pa rr, ce qui eft impoffible. Je ferai
donc Q = nq - A q 1 -, ou n & q 1 font de nouvelles
indéterminés, il en réfulte que tous les termes ont A
pourfafteur, excepté q r qui a « 2—i?;doncraa — B
doit être divifible p a r A . ainfi, toutes les fois que
n < — ne donne pas n 2— B divifible par A , le problème
n’eft pas réfoluble.
Mais fi — ^ = A \ alors fubftituant dans l’équation
en p , ç , (>, ci-deffus, la valeur de Q , on aura
une équation B y 12 + A '1 qui fera un quarré , fi
A 1 < B , nous aurons avancé la folution, finon la
tnettant fous la f o rm e l " y - + B " égal à un quarré,
& la traitant comme la propofée, nous aurons
1 ~D- , & fi n 1 < — donne une folution à caufe
de B <é A 1 , nous aurons A =■ n— ^— < A 1, &
On cherchera B '" y 2 - f A v égal à un quarré;, continuant
toujours ainfi, il eft clair que l’on trouvera
héceffairemc-nt ou équation impoffible^ i , ou 2 égal
à un quarré, ou A i Q 2 •+■ B i ‘ égal à un quarré ,
toutes équations dont on connoît la folution ; l’on
voit que toutes les fuppofitions étant linéaires, la
folution générale de la derniere équation donnera
celle de la propofée.
Des foluûons en nombres entiers. On trouvera,
en faifant les mêmes fubftitutions que dans l’article
précédent, que pour que Q 2 — A y - — B , il faut
n— A foit égale à un nombre entier n < — , & en-
fuite il faudra que C 1 A * y 2 — i B 1 Q y + C ' Q 2
— i : tous ces nombres étant entiers , ffcette équation
avoit des fafteurs rationnels,il n’yauroit pas de
difficulté,finon pour fatisfaire à cette derniere condition
; on cherchera la plus petite valeur, en
nombres entiers de la fonftion égalée à l’unité, &
fi cette valeur eft un , le problème fera poflible,
finon il ne le fera pas. Maintenant:, pour trouver ces
valeurs qui rendent la fonftion ci-deffus la plus petite
, on verra que foit -\-ym - f B y ™-1 a. .. + Q xm,
qui doit une quantité moindre-, elle fera
y - a x x y - b x ...........x y - { b ' + e y / - i )
X x y - ( b - e \ / - i ) x ( l + b ' - e ' \ / - l ) & c c . =
y — a x — b , x '!--\- e12 x 1.........donc
il faudra que .y — a x ,y -b > x x , y - b x foient moindres
que y ' - a x '.y 1 - b 1 x ’ , y 1- b x ,y 1 & * 1 étant
des nombres < y & x ; il faudra donc lavoir, a étant
un nombre donné non rationnel, quelles valeurs dey
& de * donnent à y — a x cette propriété ; pour cela
on fuppofera que foit p - a q une fonftion & s p S
q r xz — i , on aura en général r < p , & s < q p—
a q < r— a s , & < que toute fonftion x — a y ou x
eft entre p & r, Scy entre q & s, faifant donc p- = a,
& réduifant en fraftions continues, on aura les fractions
j , 7 , &c. qui jouiront de la propriété ci-
deffus ; donc fi les fraftions^,-j, &c. ou les fonctions
p — aqXp' — a 1 q ’ .....qvCon fuppofe devenir
minimum font en nombres finis , on connoîtra
le vrai minimum , fk c’eft c e qui arrive toutes les
fois que a eft rationn el, ou que la fonftion eft du
fécond dégré. V. F r a c t io n s c o n t in u e s , Suppl.
Connoiffant une ou plnfieurs valeurs de Q , de.y,
on trouvera que les autres feront données par l’équation
t 2 ^ Ê A u 2 = i , A étant une fonftion des, v a leurs
connues de Q & d e y .* o r , cette équation admet
une infinité de folutions, fi A n’eft pas négatif
Sc eft qu a r ré , & n’en admet qu’une feu le , fi A eftpo-
fitif & non quarré. Connoiffanty' & Q & toutes leurs
valeurs ; comme nous avons les quantités cherchées
égales à des fonftions linéaires de y &C d e .Q , nous
n’aurons à réfoudre que des équations indéterminées
linéaires, & l ’on trouvera que pour le cas oit il y a
un nombre infini de valeurs de Q & fatisfaifant au
problème , il fuffirade v o ir fi la folution eft poffible
pour un certain nombre de valeurs, qu’on pourra
d’après cela juger des autres.
Je me fuis borné à indiquer la folution de ce dernier
problème, dont les détails demandent des o pé rations
très-épineufes.
Je m’arrêterai peu aux degrés fupérieurs, parce
que à l’exception de ce qu’ils réfolvent par la même
méthode que ceux de Diophante , il n'y a encore
qu’un très-petit nombre d’équations particulières qui
aient été réfolues par des méthodes indirectes. L a
plus fufceptible de généralifation eft celle de M.
E u le r , qui çonfifte à trouver fucceflivement qu’il
doit y avoir des folutions en nombres plus petits
jufqu’à ce qu’on tombe à des équations que les fuppofitions
les plus fimples doivent réfoudre ; c’eft
ainfi qu’il démontre qu’on ne peut av o ir x 4 + y 4 =
m x * - y * = Q 2 , ni x i ± _ y ’ = Q h foye^
le tome I I de l ’Algèbre de M. Euler déjà cité. (0)
Méthode des çoéjfficicns indéterminés. On regarde
Defcartes comme l’inventeur de cette méthode.
Voici-en quoi elle çonfifte. Il faut d’abord cônnoître
la forme générale à laquelle doit fe réduire néceffai-
rem en t, foit l’équation cherchée, fo it une équation
d’une nature donnée , qui doit avoir lieu en même
tems qu’une équation connue. Enfuite on fuppofe
égale à zéro une fonftion indéfinie de cette forme ;
& on fait en forte qu’en y fubftituant la valeur d’une
des variables, tirée de l’équation donnée, le refte
foit identiquement égal à z é ro , ou bien que l’équation
indéfinie fatisfafle aux conditions du problème.
On a enfuite , entre les coëfficiens , des équations
qui fervent à le déterminer & à marquer le point
ou la fonftion indéfinie s’arrête ; par-là tous le problèmes
fe réduifent à connoître la forme dont eft
fufceptible l’équation définitive qu’on cherche. On
v o it delà combien cette méthode de Defcartes a
généralifé les problèmes de l’analyfe. En e ffe t, la
recherche de cette forme générale eft d’une trèsr-
grande généralité, & il y a toujours une infinité
d’équations à qui elle convient ; au lieu qu’avant
cette m éthode, on ne pou v oit connoître àpriori, ni la ,
réunion de tous les problèmes delà même c la fle , ni
l ’étendue de la méthode qu’on employoit à les réfoudre
chacun en particulier. Cette détermination de la
foi;me générale dont eft fufceptible l’équation cherchée
, & la réduftion de chaque problème à la méthode
des coëfficiens indéterminés , deviendra d’autant
plus importante dans l’analyfe , que celle-ci deviendra
plus étendue à la fin. Les géomètres feront
obligés de s’y arrêter dans bien de problèmes compliqués
; & il en naîtra une forte d’algebre, aufli fu-
périeure en généralité à l ’algebre ordinaire , que
celle-ci l ’eft à l’arithmétique. (0)
Séparation des indéterminées. On appelle équation
féparée, celle où on a une des variables égale à une
1 fonftion donnée des autres , ou une fondtion d’une
des varia b les , aufli égale à une fonftion des autres.
T ou te équation féparée , différentielle du premier
o rd re, eft intégrable par les quadratures. Auffi toutes
les méthodes d’ intégrer de Jean Bernoulli, tendent
elles àfaire des fubftitutions, telles qu’on puiffe
féparer les indéterminées dans l’équation transformée.
C e tte méthode n’eft pas g én érale , fi l’on fe borne
à des fubftitutions algébriques. Il y a d’ailleurs des
équations qui ne font pas intégrales étant fepa ré es ,
& dont on peut avoir cependant l’intégrale algébriquement.
V o y e z les Mémoires de Turin, tome I fi ; les
Mémoires de M. de la Grange.
Qu elle que foit une équation finie entre x , y , £ , '
on peut toujours regarder £ comme une fonftion de
x , y .* mais lorfque l’équation contient des tranfcen-
dantes , il y a une infinité de cas où l’on ne peut e xprimer
cetre fonftion par un nombre fini de termes.
Et lorfqu’on a deux équations entre trois variables ,
il peux a r r iv e r , dans ,1e même cas , qu’il foit impofli-
ble d’en éliminer une fans différentier. C e la vient de
c e que appellant = .V o , V = , o , les deux équations,
S i Z la fonftion, qui après l’élimination feroit égalée
à z é ro , on à toujours Z égal à une fonftion de Ÿ
& de V \ Mais l’élimination n’eft: poflible que lorf-
que cette fonftion de V & V ' eft exprefiible ert
termes finis ; e’eft-à-dire* lorfque l’équation eft Z ,
K , V eft féparable ; lorfqu’elle ne l’eft pa s, & que
dV^ d K font algébriques, on peut fuppofer que
A d V -p A ' d V ' foit une différentielle e x a fte , telle
que l’égalant à zéro , on puiffe en tirer ^en x >y ; &C
par con féq uen t, en fubftituant dans les'équa tion s
V — Q, ou V = 0 , l’équation cherchée en x \ y ,..on
au ro it, par -les mêmes moyens, l’équation qui a lieu
en r , { , & en y , £ , lorfqu’elle eft poflible en termes
finis. Voyc^ l’article In t é g r a l ci-deffus ; & les
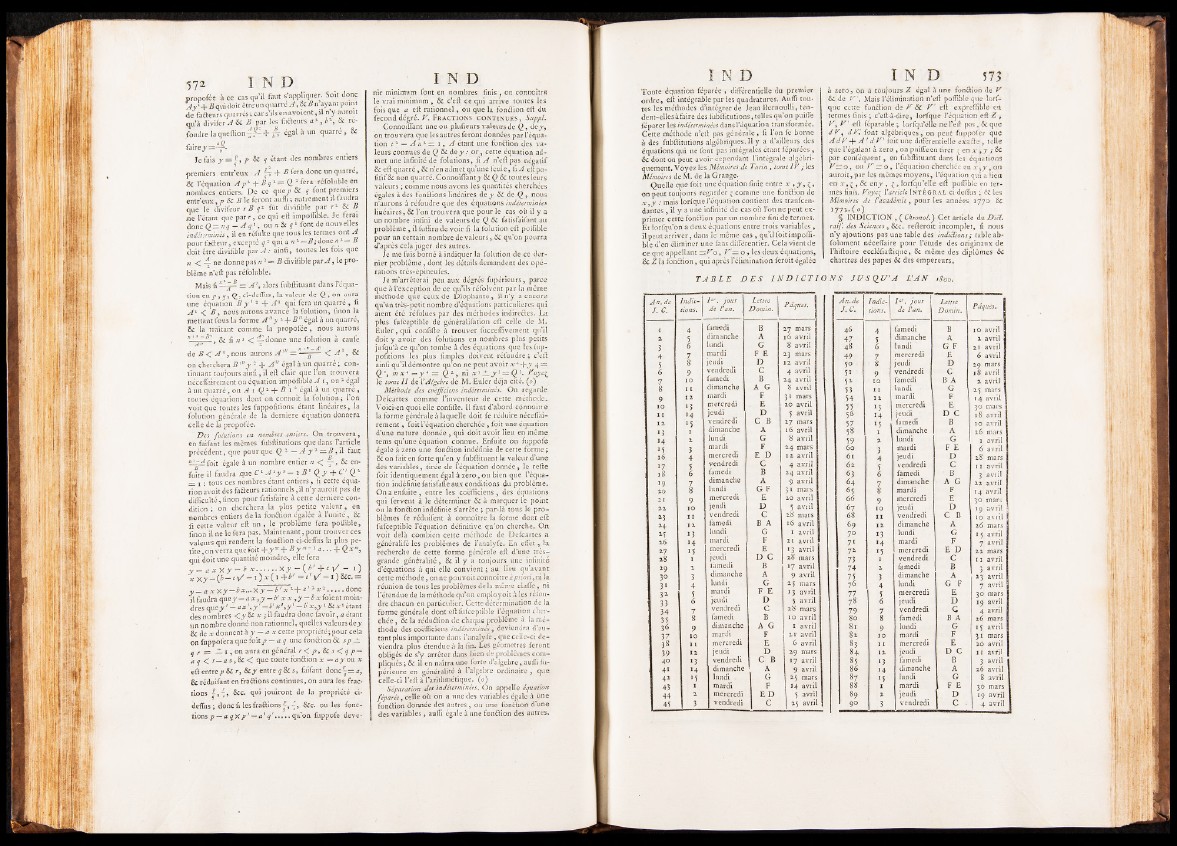
Mémoires de Üacadémie, pour les années 1770 ÔC RflD I § IN D IC T IO N , ( ChronoL') C e t article du Dicl.
raif. des Sciences, Sic. refteroit incomplet, fi nous
n’y ajoutions pas une table des indiclions; table ab-
folument néceffaire pour l’étude des originaux de
l’hiftoire eccléfiaftique, & même des diplômes Sù
Chartres des papes ÔC des empereurs*
T A B L E D E S I N D I C T I O N S J U S Q U ' A L 'A N 1800*
A n . de
J. C.
Indictions.
I er. jour Lettre 1
D om in .\ Pâques.
An.de
L C .,
Indictio'ns.
de Van.
Lettre
Domin.
Pâques.
1 4 famedi B 27 mars 46 4 famedi B 10 avril
2 5 dimanche A 16 avril 47 dimanche A 2 avril
3 6 lundi G 8 avril 48 6 lundi 1 G F 21 avril
4 7 I mardi F F. 23 mars 49 7 mercredi E 6 avril
5 8 jeudi D 12 avril ! f o 8 jeudi D 29 mars
6 I 9 vendredi C 4 avril 51 9 vendredi C
10 famedi B 24 av ril > 5Z famedi B A
g . 11 dimanche A G 8 avril 53 1 1 lundi • G
9 12 mardi F 31 mars 54 12 mardi F 14 avril
10 *3 t mercredi . E 20 avril 55 13 ■ mercredi E 30 mars
11 H jeudi D 5 avril ■ 14 jeudi D C 18 avril
12 vendredi C B I 27 mars 57 15 famedi B 10 avril
J 3 1 dimanche A 16 avril 58 1 dimanche A - 26 mars
H 2 lundi G 8 avril 59 2 lundi G 1 avril
mardi F 24 mars 60 mardi F E
16 4 mercredi E D 12 avril 61 4 jeudi D 28 mars
5 vendredi C 4 avril 62 5 vendredi C
iS 6 famedi B 24 avril 63 6 famedi B
19 7 dimanche A 9 avril 64 7 dimanche A G 22 avril
20 8 lundi G F 3 1 mars 6 5 8 mardi F
-ÆX 9 mercredi E 20 avril 66 9 mercredi E 30 mars
22 10 jeudi D 5 avril 67 10 jeudi D I Tp ?v r;i 1
11 vendredi C 28 mars 68 11 vendredi C B
24 12 famedi B A 16 avril 69 12 dimanche A 26 mars
M 13 lundi G 1 avril 70 n lundi G 1 5 avril
26 14 mardi F 1 1 avril 7 1 *4 mardi F 7 avril
27 15 mercredi E 13 avril 7 * 15 mercredi E D 22 mars
28 1 jéuai , ; D C z8 mars 73 1 vendredi C 11 avril
2, famedi B 17 avril 74 2 famedi B
3° 3 dimanche A 9 avril 75 3 dimanche A 23 avril
31 4 lundi G 2.5 mars 7$ 4 lundi G F 7 avril
32 5 mardi F E 13 avril 7 7 5 mercredi E 30 mars
33 6 jeudi D 5 av ril 78 6 jeudi D 19 avril
34 7 vendredi c z 8 mars 79 7 vendredi G 4 avril
35 8 famedi B 10 av ril 80 8 lamedi B A 26 mars
36 9 dimanche A G 1 avril 81 9 lundi G 15 avril
37 10 mardi F 2i* avril 82 10 mardi F 31 mars
38 11 mercredi E 6 avril 83 11 mercredi E 20 avril
39 12 jeudi D 29 mars 84 12 jeudi D C 11 avril
40 *3 vendredi C B 1 7 avril 85 13 famedi B 3 avril
4 » H dimanche A 9 avril 86 14 dimanche A 26 avril
42 *5 lundi . G z 5 mars 9 15 lundi G 8 avril
43 1 mardi F 14 avril 88 1 mardi F E 30 mars
44 2 mercredi E D l 5 avril ; 89 % jeudi D 19 av ril
45 3 vendredi C 25 avril ■ 90 3 vendredi C 4 avril