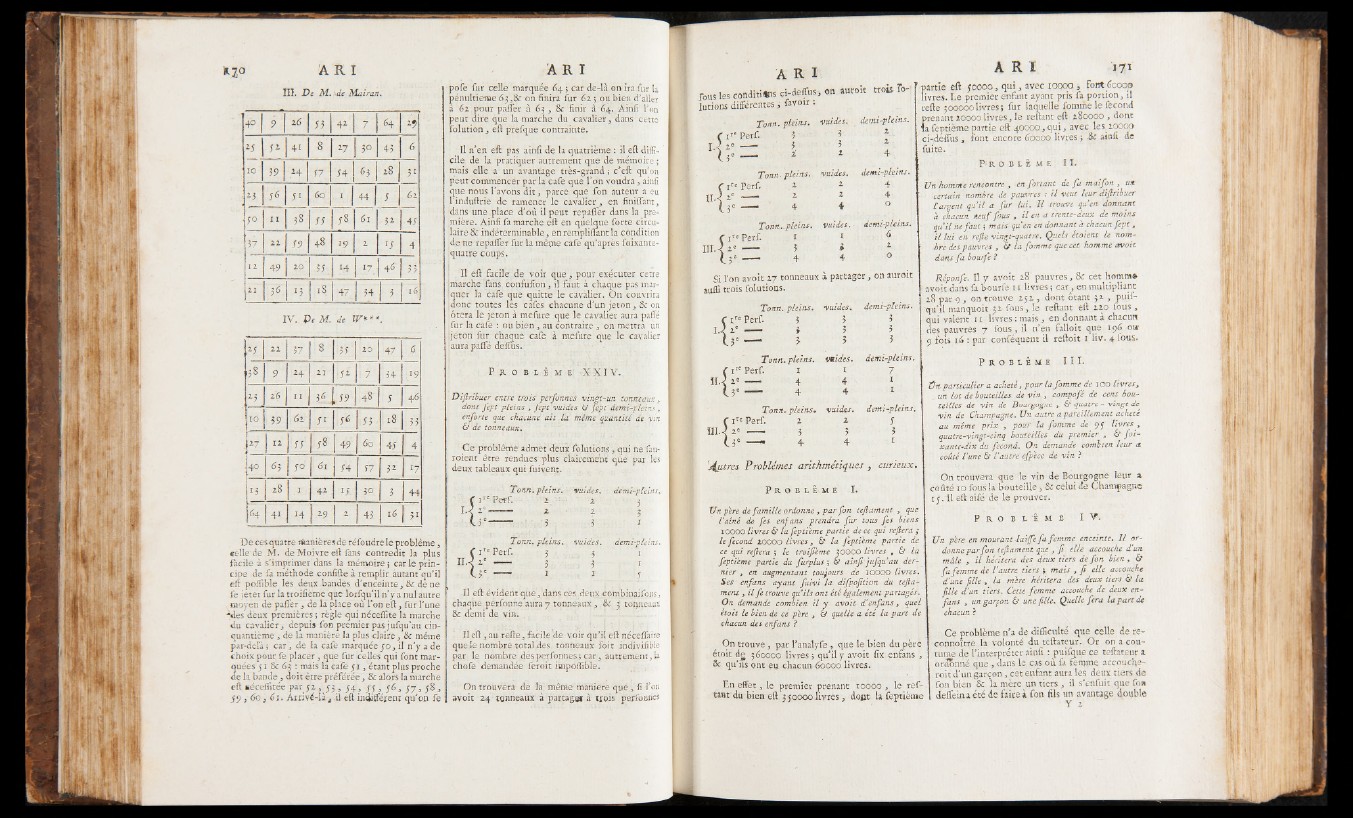
Hl. De M. \de Mairan.
40 9 16 S i 41 7 ' é4 ^9
1 •î * 41 8 ^7 3° 43 6
10 39 ,24 37 » 63 18 i 1
56 Ji 60 ■r>fï J 44 >1. 6z
38 SS 38 6l 31 43
37 22 5 9 48 19 2 .13 4
12 49 10 .33;. 14 17. 46' 33
21 36 13 ,18 47 1 34 3 l6
IV . De M. de IF * * * .
23 22
-sJ
CO
53 20 47 6
*38 9 H MB 1 ■ 34 19
2 3 26 II 3A m 48 : 3 46
10 39 6z 31 j 36 )3 i . } | j: 33 Nj 12 'SS' 38 49 60 43^ 4
4° 6i ' S<f i 61 34 \ 37 31 ' 17
i 28 I jjÉ! 3. 3». 3 44
64 4 i H 19 2 43 l6 J yi
De ces quatre Manières de réfoudre le problème,
celle*de M. de Moivre eft fans contredit la plus
facile à s'imprimer dans la mémoire 5 car le principe
de fa méthode confïfte à remplir autant qu'il
eft poflible les deux bandes d'enceinte , & de ne
fe jeter fur la troifième que lorfqu'il n'y a nul autre
moyen de palier , de la place où l'on eft , fur l'une
■ •des deux premières ; règle qui néceflïte la marche
du cavalier ^ depuis fon premier pas jufqu’aù cinquantième
, de la manière la plus claire , & même
par-delà > car , de la café marquée y o , il n'y a de
choix pour fe placer , que fur celles qui font marquées
51 & 63 : mais la café y 1 , étant plus proche
de la bande , doit être préférée, & alors la marche
eft séceffitée par 5 2 3 53 , 5 4 3 y y , y6 3 y ? 3 y8 ,
59 360 3 é i . Arrivé-làa i l eft indifférent qu'on fe
pofe fur celle marquée 64 j car de-là on ïra.fur la
pénultième 63,& on finira fur 62 ; ou bien d'aller
a 62 pour palier à 63 , & finir à 64. Ainfi l'on
peut dire que la marche du cavalier .3 dans cette
îolution , eft prefque contrainte.
Il n'en eft pas ainfi de la quatrième : il eft difficile
de l,a pratiquer autrement que de mémoire ;
mais elle a un avantage très-grand ; c'eft qu'on
peut commencer par la café que l'on voudra , ainfi
que nous l'avons dit 3 parce que fon auteur a eu
l'induftrie de ramener le cavalier 3 en finiffant
dans une place d'où il peut repàffer dans la première.
Ainfi fa marche eft en quelque forte circulaire
& indéterminable, en rempliffant la condition
de ne repalfer fur la même café qu’après foixante-
'quatre coups.
Il eft facile de voir que 3 pour exécuter cetre
■;marche fans confufion , il faut à chaque pas marquer
la café que quitte le cavalier. On couvrira
(donc toutes les cafés chacune d'un jeton , & on
ôtera le jeton à mefure que le cavalier aura paffé
fur In café : ou bien , au contraire , on mettra un
{jëton fur chaque café à mefure que le cavalier
aura paffe defîus.
P R O B L È M E 1 - X X I V . ,
Diftribuer entre trais perfonnes vingt-un tonneaux 3
dont fept pleins 3 fept.vuides & fept demi-pleins,
enforte que chacune ait la même quantité de vin
& de tonneaux.
C e problème admet deux folutions , qui ne fau-
roient être rendues plus clairement que par les
deux tableaux qui fuivent.
H
1
Tonn. pleins.
i re Perl. - 2 /---
Tonn. pleins.
i re Perf. 3
1 ----- 1
vuides.
2
1H
vuides.
I 3
; 3
, 1
demi-pleinsK
“ 3g
demi-pleins.
5
Il eft évident que , dans ces.deux combinaifoiis,
chaque perfonne aura 7 tonneaux , & 3 .tonneaux
& demi de vin.
Il eft ^ au refte , facile de voir qu'il eft néceffaire
que Je nombre total ides tonneaux foit ind.ivifibie
par le nombre des perfonnes.; car, autrement, la
chofe demandée feroit impoffible.
On trouvera de la même maniéré qué., fî l'on
ayoit 24 tonneaux à partaggt à trois perfonnes
Æ les conditions ct-deffas, on. auroit « o i s . | |
lutions différentes j favoir .
Tonn. pleins. •vuides. demi-pleins.
I 1* Perf. 5 3 2 .
2e 3 2
3 e ---- - 2 1 4'
Tonn. pleins. vuides. demi-pleins.
Ir<■ P e r f 1 2 4
2e __ _ 2 2 4
------ 4 4 0
Tonn.-pleins. vuides. demi-pleins.
‘ Perf. 1 I 6
2 e - . — y m . 2
— 4 4 0
Si Ton avoit 27 tonneaux à partager 3 on auroit
aufli trois folutions.
Torrn, pleins. ■vuides. demi-pleins.
C i ro Perf. ? 3 3
1.4 2' ----- i 5 3
1. 3e ----- î 3 3
Tonn. pleins. vetides. demi-pleins.
( 1« Perf/ ' i 1 7
n .4 2 ' — 4 4 1
\ i ° ----- 4 4 1
Tonn. pleins. vuides. demi-pleins.
f 1 " Perf. 2 - 2 S
Ï I I .4 2 ' ----- 3 3 ■ 3
( . 3e ----- 4 4 1
'/£utrçs Problèmes arithmétiques , curieux.
P r o b l è m e I.
partie eft y0000 3 qui 3 avec 10000 , font 60009
livres. Le premier enfant ayant pris fa^portion, il
refte 300000livres} fur laquelle fomme le fécond
prenant 20000livres, le reliant eft 280000, dont
la feptième partie eft 40000, qui, avec lesAOOOO
ci-deffus, font encore 60000 livres } .& ainfi de
fuite.
P r o b l è m e I I .
Un homme rencontre 3 en fortant de fa mai fon , un
certain nombre de pauvres : il veut leur diflribuer
üargent quil a fur lui. I l trouve qu’en donnant
a chacun neuf fous , il en a trente-deux de moins
quil ne fa ut} mais quen en donnant a chacun fept 3
il lui en refte vingt-quatre. Quels êtoient le nom-
f. bre des pauvres , & là fomme que cet homme avoit
dans fa bourfe ?
Réponfe. Il y avoit 28 pauvres, & cet homm*
avoit dans fa bourfe m livres ; ca r , en multipliant
28 par 9 , on trouve 2y2 , dont ôtant 3 1 , puif-
qu'il manquoit 32- fous, le reliant eft 220 fous ,
qui valent 11 livres : mais , en donnant à chacun
des pauvres 7 fous, il n'en falloir que 196 01*
9 fois 16 : par conféquent il reftoit 1 liv. 4 fous.
P r o b l è m e I I I .
Ün particulier a acheté, pour là fomme de IOO livres3
_ un lot de bouteilles de vin , compofé de cent bouteilles
de vin de Bourgogne , & quatre - vingt afe
vin de Champagne. Un autre a pareillement acheté
au même prix y pour la fomme de 95 livres ,
quatre-vingt-cinq bouteilles du premier 3 & fo i-
xante-dix du fécond. On demande combien leur a
coûté l ’une & Vautre efpêee de. vin ?
On trouvera que le vin de Bourgogne leur a
coûté 10 fous la bouteille, & celui de Champagne
iy . Il eft aifé de le prouver.
Un père de famille ordonne , par fon teftament , que
Vaine de- fes enfans prendra fur tous fes biens
IOOOO livres & la feptième partie de ce qui reftera ,*
le fécond 2.0000 livres 3 la feptième partie de
ce qui reftera } le troifième 30000 livres , & la
feptième partie du furplus 3 6? ainfi jufqu au dernier
3 en augmentant toujours de IOOOO livres.
Ses enfans ayant fuivi la difpofition du teftament
3 il fe trouve quils ont été également partagés.
On demande combien il y avoit d'enfans 3 quel
etoit le bien de çé père , & quelle o. été la part de
chacun des enfans ?
On trouve, par l'analÿfe, que le bien du père
étoit de 360000 livres} qu'il y avoit fix enfans ,
& qu'ils ont eu chacun 60000 livres.
En effe t, le premier prenant 10060, le ref-
tant du bien eft 3 y0000 livre s , dont la feptième
P r o b l è m e I ^
Un père en mourant daiffe fa femme enceinte. I l ordonne
par fon teftament que 3 fi elle accouche d un
mâle 3 il héritera des deux tiers de fon bien, &
fa femme de Vautre tiers } mais , f i elle accouche
. d’une fille 3 la mère héritera des deux tiers & la
fille d'un tiers. Cette femme accouche de deux enfans
3 un garçon & une fille. Quelle fera la part de
chacun ?
Ce problème n’ a de difficulté que celle de re-
connoître la volonté du teftateur. Or on a coutume
de l'interpréter ainfi : puifque ce teftateur a
ordonné q ue , dans le cas où fa femme accouche-
roit d’ un garçon, cet enfant aura les deux tiers de
fon bien & la mère un tiers , il s’enfuit.que fo»
deffeina été de faire à fon fils un avantage doiibie
y %