*92 C A U
par une ligne , après avoir barr-é le 6 , -romme
«ans l’eccemple fui vaut :
Le calcul étant ainfi terminé , la première
ligne de chiffres doit indiquer le premier mot
du vers latin que l’on cherche, la fécondé doit
indiquer le fécond mot , &c.
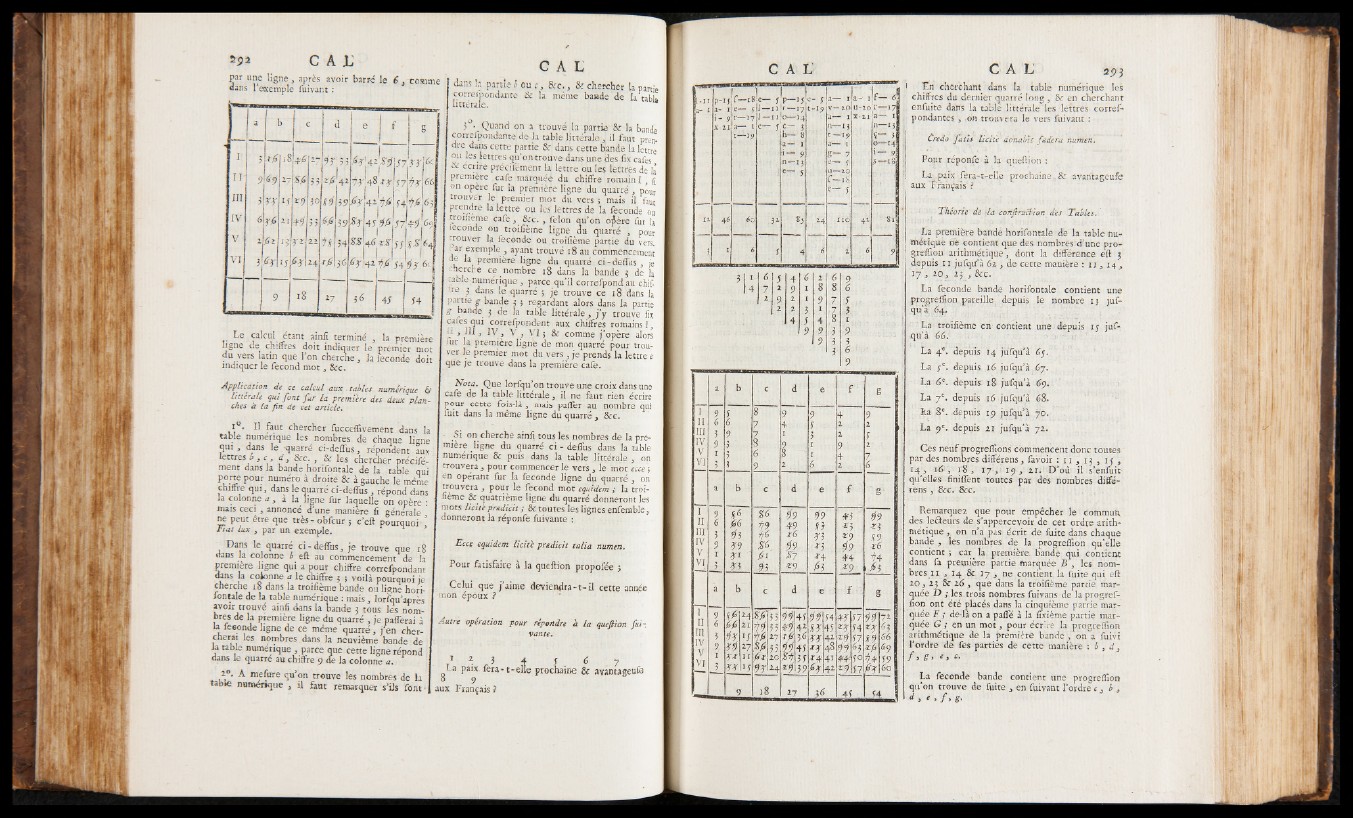
Application de ce calcul aux. tables numérique &
littérale qui font fur la première des deux planches
a la fin de cet article.
i Q. Il faut chercher fuccefïivement dans la
table numérique les nombres de chaque ligne
qui y dans le •quarré ci-deffus 3 répondent aux
lettres b 3 c■ , d 3 &c. , & les chercher précifé-
ment dans la bande horifontale de la table qui
porte pour numéro à droite & à gauche le même
chiffre qui, dans le quarré ci-deffus, répond dans
la colonne a 3 à la ligne fur laquelle on opère :
mais c e c i , annoncé d’une maniéré fi générale
ne peut être que très - obfcur 5 c’eft pourquoi "
Ftat lux 3 par un exemple.
Dans le quarré ci - deffus, je trouve que 18
dans la colonne b eft au commencement de la
première ligne qui a pour chiffre correfpondant
dans la colonne * le chiffre 3 ; voilà pourquoi je
cherche 18 dans la troifîeme bande ou ligne hori-
fontale de la table numérique : mais, lorfqu’après
avoir trouvé ainfi dans la bande 3 tous les nombres
de la première ligne du quarré , je pafferai à
la fécondé ligne de ce même quarré , je n chercherai
les nombres dans la neuvième bande de
la table numérique , parce que cette ligne répond
dans le quarré au chiffre 9 de la colonne *.
2°. A roefure qu’on trouve les nombres de la
table numérique , il £mt remarquer s’ils font-
C A L
dans la partie b ou c , & c . , & chercher la partie
correijpondante & la même bande de la tabla
3°. Quand on a trouvé la partie & la bande
correspondante de la table littérale, il faut prendre
dans cette partie & dans cette bande la lettre
ou les lettres qu’on trouve dans une des fix cafés
& écrire précilement la lettre ou les lettres de la
première café marquée du chiffre romain I , jf
on opéré fur la première ligne du quarré , pour
trouver le premier mot du vers > mais il. faut
prendre la lettre ou les lettres de la fécondé ou
croifieme ca fé , & c . , félon qu’on oj$ère fur la
fécondé ou troifième ligne du quarré , pour
trouver la fécondé ou.troifième partie du vers,
ar exemple , ayant trouvé 18 au commencement
de la première ligne du quarré ci -deffus , je
cherche ce nombre 18 dans la bande 3 de la
tab^e-numérique , parce qu’il correfpond au chif-
,re 3 dans le quarré ; je trouve ce 18 dans la
partie ƒ bande 3 j regardant alors dans la partie
g bande 3 de la table littérale , j’y trouve fix
cafés qui correfpondent aux chiffres romains I ,
i l , I I I , IV , V , VI j & comme j’opère alors
lur la première ligne de mon quarré pour trouver
le premier mot du v e rs , je prends la lettre e
que je trouve dans la première café.
Nota. Que lorfqu’on trouve une croix dans une
café de la table littérale, il ne faut rien écrire
pour cette fois-là, mais palier au nombre qui
fuit dans la même ligne du quarré , & c .
• Si on cherche ainfi tous les nombres de la première
ligne du quarré ci - deffus dans la table
numérique & puis dans la table littérale , on
trouvera , pour commencer le vers , le 'mot ecce )
en opérant fur la fécondé ligne du quarré , on
trouvera , pour le fécond mot equidem ,* la troi-
fïeme & quatrième ligne du quarré donneront les
mots licite pr&dicit ; & toutes les lignes enfenable,
donneront la réponfe fui vante :
Ecce equidem licite pr&dicit talia numen.
Pour fatisfaire à la queftion propofée 5
Celui que j ’aime deviendra - t - il cette année
mon époux ?
Autre operation pour répondre a la queftion fui'’,
vante.
T ' 1-7 »T ' . ü „ .7
L a paix, f e r a - 1 - e l l e prochaine & avantageufe
8 9
aux Français t
C À L
3 1 1 6 5 4 6 2 6 9
[4 -,7 2 9 1 8 8 6
2 9; Ë * ! 9 .7 y
9 9 3 9
9
C A L
> En cherchant dans la table numérique les
chiffres du dernier quarré long, & en cherchant
1 enfuite dans la tablé littérale les lettres corref-
pondantes i on trouvera le vers fuivant :
Credo fatis licite' dcnabit f&dera numen.
Pour réponfe à la queftion :
La-paix fera-t^elJe prochaine ~ & avaritageufê
aux Français ?
Théorie de 'la confirùclion des Tables.
La première bande horifontale de la table numérique
ne contient que des nombres d’ une pro*
greffon arithmétique, dont la différence eft 3
depuis 11 jufqtf’à 62 , de cette manière : 1 1 , 14 ,
'17 , 20 , 2 3 , &c.
La fécondé bande horifontale contient une
pmgreffion pareille depuis le nombre 13 juf-
qu’ a 64f
La troifième en cofttient une depuis ic juf-
qu’à 6 6 ; -•
La 4*. dèpuis 14 jüfqu’ à 65.
La ; e. depuis 16 jufqu’ à .67. ,
La 6e. depuis: 18 jufqu’à 69.
La 7e. depuis 16 jufqu’à 68.
La 8e. depuis 19 jufqu^à 70.
La 9e. depuis 21 jufqu’ à 72.
Ces neuf progreffons commencent donc toutes
par des nombres différens , favoir : 1 1 , 1 3 , 1 c ,
1 4 , 1 6 , 18, 1 7 , 1 9 , 2 1 . 'D’où il s’enfuit
qu’elles finiflènt toutes par des nombres différens
y & c . & c .
Remarquez que pour empêcher le commué
des le&eurs de s’appercevoir de cet ordre arithmétique
, on n’a pas écrit de fuite dans chaque
bande , les nombres de la progreflion qu’elle
contient î car la première, bande qui contient
dans fa première partie marquée B , les nombres
11 , 14 & 17 , ne contient, la fuite qui eft
20 , 23 & 2 6 , que dans la troifième partie marquée
L>, les trois nombres fuivans de la progref-
fion ont été placés dans la cinquième parrie marquée
F ; de-la on a paffé à la fixième partie marquée
G ; en un m o t, pour écrire la progreflion
arithmétique de la première bande , on a fuivi
l’ordre de fes parties de cette manière : b , d ,
f > g y * , c -'
La fécondé bande contient une progreflion
qu’on trouve de fuite , en fuiyant l’ ordre c 3 b 3
d y * >f> g*