il 2 0 A R I
mente de. l’ unité. On en a des exemples dans 9 ,'
2ƒ 3 49 j 81 , &c. defquels ôtant 1 , le refte eft
divifible pat ©1 :
I V. !
Tout nombrè eft ou quarré 3 ou divifîble en
d eu x , ou trois, ou quatre quarrés, Ainfi 30 èft
é£al à z ; + 4 + 1 ; 3 1= ? 25 -h 4 -+-1 -h 1 î
3,3 *+■ 16 H- 1 } 63 == 49 - f - 9 4 1 , ou
3*6 -+- 1 *4- x •
Rajouterai ici 3 par anticipation, quoiqu’on fie.
fçache pas encore ce que, c’eft que nombre triangulaire,
pentagone, occ que
Tout nombre eft ou triangulaire , ou compofé
de deux ou trois triangulaires.
Il eft ou pentagone, ou compofé de deux, ou
trois, ou quatre, ou cinq pentagones} & ainfi
des autres.
Rajouterai enfin que tout quarré pair , hors
lè premier 1 , eft refoluble au moins en quatre
quarrés égaux} & que tout quarré impair l’eft au
moins en trois , s’il ne l’eft en deux. Ainfi 81 =
36-+- 36 -4-5)} f i l ==81 4 - 36-4- 4} 169 = 1444-
23} 623 ==400 4 - 144 4 - S i.
B v.;
Toute puifîance de cinq ou de fix , finit né-
ceffâitèmeht par cinq ou par fix.
V I.
Si on prend deux nombres quelconques , l’un
des deux, ou leur, fomme, ou leur différence,
eft néceffairement divifîble par trois. Soient pris
les nombres 20 & 17 } aucun d’ eu x , ni leur
fomme 3 7, n’étant pas divifîble par 3 , leur différence
l ’e ft, cat elle eft trois.
Il eft aifé de démontrer que cela doit arriver
néceffairement, quels que foientles nombres qu’oii
prendra. ,
Y t l .
Si deux nombres font tels, que leurs quarrés
ajoutés enfemble faffent un quarré , le produit
de ces deux nombres eft divifîble par 6.
• Tels fo n t, pour en donner un exemple, les
nombres 3 & 4 , dont les quarrés 9 & 16 ajoutés
enfemble font lè nombre quarré 2y : leur produit
12 eft divifîble ■ par 6.
La démonftration générale de cette propriété
A R 1
ne fçàuroit trouver place i c i } mais l’on peut tiret
de ce qu’on vient de d ir e , un moyen de
Trouver deux nombres dont les quarrés ajoutés
enfemble faffent un nombre quarré. Pour cet effet,
multipliez deux nombres quelconques ; le double
de leur produit fera l’ un des deux nombres
cherchés, & la différence de leurs quarrés fera
l’autre.
Comme fî l’on multiplie l’un par l’autre ces
deux nombres 2 ; 3 , dont les quarrés font 4 ,
•9, leur produit fera 6 , dont le double 12 , &
la différence de leurs quarrés 5 , font deux nombres
tels que la fomme de leurs quarrés ëft égalé à
un autre nombre quarré : car ces quarrés font
144 & 2j , qui font 16 9 , quarré de 13.
y r 1 1.
Lorfque deux nombres font te ls , que la dift
férence de leurs quarrés eft un nombre quarré ,
la fomme & la différence de ces nombres font
elle-mêmes un nombre quarré, ou le double.
Tels font, par exemple , les nombres 13 8c
■ 113 dont les quarrés font 1 6 9 ', 1 4 4 , dont la
différence eft 23 , qui eft auifi un quarré } la
fomme de ces nombres eft 23, nombre quarré.
Les nombres 6 & 10 ayant pour quarrés 3 6
& ï.oo., dont la différence eft 64, nombre quarré;
on trouve que leur fomme eft 16 , qui eft auflà
un nombre quarré, ainfi que leur différenCè 4. •
Les nombres 8 & 10 ayant des quarrés dont
la différence eft 36, on voit auffi que la fomme
de ces nombres eft 1 8 , qui eft double de 9 9
nombre quarré } & leur différence 2 eft le double
de 1 , nombre quarré , & c .
I X.
Si on multiplie deux nombres dont la différence
eft 2 , leur produit augmenté de d’unité
fera le quarré du nombre intermédiaire.
Ainfi de produit de 12 par 14 eft 168, qui,
augmenté de 1 /donne 16 9, quarré de 134 nombre
moyen entre 12 & 14.
Rien n’eft plus aifé que de. démontrer que cela
doit toujours arriver} & l’on verra qu en général
le produit de deux nombres , augmenté du
uarré de la demi-différence, donne te qüarré
u nombre moyen.
X.
On appelle nombre premier, celui qui n’a d’aum
A;R I
tre divifeur que l’unité. ,-Les -nombre^ de. cette^
efpèce ne peuvent donc- être pairs , a 1 exception
du nonfhrè; deux ; niêtre 4érrrunes- par_cinq;,
excepté le qombre’ cinq lû'i-memè, |d ou ul fuit
eu a l’exception ‘de! ceux qui i l l rerjferaies daqs^
la première rpixainè, ils:; doivent- riéj:e^aï*fîmei^
fe terminerfpar 1 , ou' 5/011 7 ', . ’ou 9.
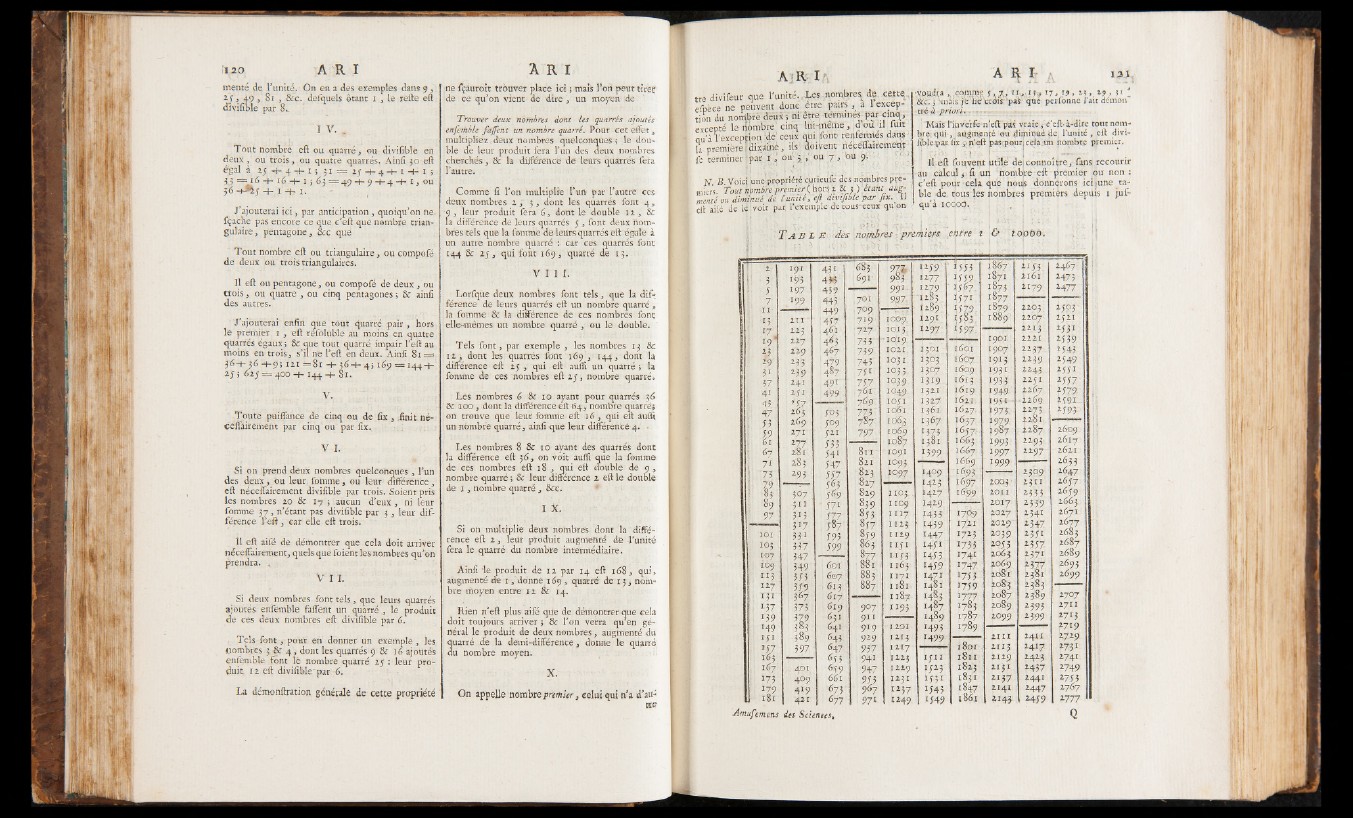
v B, Voic{ june-propriété curieufé desjnômbfes premiers.
Tout nombre premierf hors 1 & j ) 'étant augmenté
ou diminué de r unite, eft diyifible par ftx . Il
eft ailé de l é voir pari l’exemple de cous-ceux qu on
A $ It
•y pjld ra ,(tçcunme f , / 1 ir^.,13^ 1 7 , 19, 25, 19 , 31 *
miàis je né'crdis' 'pa&gùc perfonne l’ait démon“
ttéà priori. .
Mais rinverfe-nîeff pds vraie /c’eft- à-dire tout nom-
b;re< qui-, augmenté ou ^imiiiûé de, l’unité, eft divi-
fîblêipar fix p n’eft passeur: cda:un jiombre premier.
Il eft foulent (itile de| connoîtjre, fans recourir
au c a l c u l f i u4 !nombre eft premier pu non:
c’eft poiir cela que noujs donnèrent iciiune tablé
4 e. tjousTes fiombres première depuis 1 juf-
qu’ à.i.oqoô. " ‘
T a b L E ’dès [nopihres l 'premiers ektr.e t & l o'obo.
2 I # 4 3 1 1(583 9Z4 323 9 ' h s 3 i 8&7 2 I 3 3 ' 2467.'
3 lC)j 436 | 69 V 983 «27 7 - 2359 i%j i 2161 2473
j i?7 '- 459 99'J- I279 B 2I79 4477
7 I99 443 [7^ : - 9 3 7 t H É o77
11 449 i7 °%. ^89. 1879;. 2 2.0 3 23° 3
13 2TI 1437 7 ‘ 9 ' jopp. i 291 18891 2207- i j2 !
ï'7 223 1 46Ï ■ 777-1 iO.1,3. t 29 7 ' x3 9 7 . ü 23,3*
i ')* : ïiÿ * 483 ’733“ "iO'19 ipp? 2221 2339
m 2'29. 4^7 1739 1021 I3OI ié o i 1907’ 223 7 - *343
i-9 ' M ! 479 1743 I0'3I 13913 ï Gôj . 39*13’ 2 1 39 2 349
3 * 2 39 : 487 731 m M 1397 160.9 Ü B 22.43 23 3 *
37 24I 4 9 1 7 5 7 ' 1039 I 3 I9 1613 3933 221! 233z ;
4 1 23 i 499 :7(Sr“ 1321 1619 *949- 116,7 2379.
43 1 * 5 7 : 7% : lOy.I • \W k î6 21 193* - -I269 W m
47 2% 5°5 W io ’6i Î36I 1627- *973; 2273 . 4393
33 269 509 ; 787: ioë($ 1 3fi-7 I<237 1979 228I
m 27 i S11 797 i<m 1 373 l é 37H ï p 7 2287 2609-
61 27 7 533 IQ87 I38I 1663 :. I 1993. 2293 26I7
67 281 5 4 1 8i t - 1091 1 399 I667 1997 2.297 2621
7 X H 547 821 1093 16.69 . ' *999 i6 i )
7 3 ' 2 93 : 337 82î H ?4 ° 9 16933 23°9 : 2é47
79 ' 565 827 ?4 23: 16-97 | 2003'; 23ï i - 263 7 '-
-83 307. 3%', io 19 I I.O3. I x4 27 îSy) 2011 23.3 3 2é39
89 -3 n ^ 5 7 1 §39 1 109 x4 29 2037 2539 2663
97 313 577 n j “ 17 H 33 i 7.99 2027 2.341 267I
3 B 387 ^57 I I 2 3 1439 mm 2029 2 347 2677
loi- 331 593 §39 II29 1447 x7 2 3 £939 233* 2683
D| 337 599 863 W B ü 173-3 2°33 2 3 3 7 2687
*®7- 347 877 I l 3 3 1433, I7 4 1 2063 237* 2689
roo 349 I 6oï ! 8«I l i é } x4 3 9 . x74ÿ. 3069 2 377 2693
ü 3J3 607 885 " Z 1 ‘ 471 !733 268 r 2.381 l ( > 9 9
I27 ; 339 613 887 1 18 1481 1739 io fo 23 |3
151 i 367 é i y 1187 1483 1777 2087 2-389 2707
*37 1 373 619 ■ 907 1193 I4o7 1783 2089 2 393 27 l i
*39 *Z9 631 9 11 1489 1787 2°9 9 2 399 27*3
B S 303 641 ' 919 1 201 x493 1789. 27 *9
*3 * 389 643. ■ 9 29 ?2 I 3 1499 2111 24H 2-71 9
*57 397 647 9 3 7 x 2I7 1802 111$ 24 *7 m 1
l 6 5 é 33 941 H23 i j n l8 II 2129 24 23 27 4 i
16 j 4OI 649 947 1229 J32 3 l823 2ï 3 ï 2437 2749
7 3 4Ô9 6iS 1 933 I23x 1931 1831 2X37 24 4 i 2733
’ Z9 419 673 ’ , 9<57 M Ê ‘ 343 1847 2141 2447 2767
181 42 I 677 971 1249 x349 1861 »143 2439 2777