On joue à jeu égal, lorfque les mifes qu’ on dé-
pofe font en proportion directe des probabilités
qu’ il y a de gagner l’argent mis au jeu : car jouer à
jeu égal-, n’eft autre chofe que depofer une mife
tellement proportionnée avec la probabilité qu’ on
a de gagner, qu’après un très-grand nombre de
coups on fe trouve à-peu-près au pair : or il faut
pour cela que les mifes foient proportionnelles au
degré de probabilité que chacun des joueurs a en
fa faveur. Suppofons, par exemple, que Pierre
parie contre Jacques pour un coup de d es, & qu’il
y ait pour lui deux événemens & un pour Jacques;
le jeu fera égal f i , après un grand nombre de
coups , ils fe retirent a-peu-près fans perte. O r ,
y ayant deux cas pour Pierre & un pour Jacques,
après trois cens coups,Pierre en aura gagné à-peu-
près deux cens, & Jacques une centaine. Il faut
donc que Pierre dépofe i , & Jacques un feule-.
ment : car par-là Pierre, gagnant deux cens coups,
gagnera 200; & Jacques, gagnant cent coups ,
gagnera auffi 200. Aufii s’exprime-t-on , en parèil
cas, ordinairement en aifant qu’ il y a deux contre
un à parier pour Pierre.
P r o b l è m e I.
Dans le jeu de'croix ou pile , quelle probabilité y a-t-il
d'amener plu.fiej.rs fois de fuite croix , ou plufeurs
fois de fuite pile y ou bien en jouant avec plufeurs
pièces , quelle probabilité y a-t-il au elles fe trouveront
toutes croix ou toutes pile ?
Tout le monde connoît le jeu de croix ou pile ,
ainfi il eft fuperflu d’en donner ici l’explication ;
nous paftons tout de fuite à l’analyfe du problème.
Il eft évident, i ° . que n’ y ayant aucune raifon
pour que croix arrive plutôt que pile, ou pile que
c roix , la probabilité que l’un des deux arrivera
eft égale à ou qu’il y a également à parier pour
ou contre.
Mais fi l’ on jouoi t deux coups, | f que quelqu’ un
pariât d’amener les deux fois croix, pour (avoir
ce qu’ il devroit mettre au jeu , il fâudroit faire
-attention que toutes les combinaifons de croix ou
p ile, qui peuvent arriver dans deux jets conféçu-
tifs de la même pièce y font croix-, croix > croix ,
pile y pile, croix : pile , pile ; dont une feule donne
croix j croix. Il n’y a donc qu’ un ca§_ fur 4 qui
f ît gagner celui qui parieroit d’amener deux fois
de fuite croix : la probabilité de cet événement
ne feroit conféquemment que f ; & celui qui par
rieroit pour -, ne devroit mettre au jeu qu’un é cu ,
par exemple, pendant que l’autre en mettroittrois :
.car ce dernier auroit trois, cas pour gagner , pen-;
dantque le premier n’en a qu’ un. Ainfi leursmifes,!
pour jouer à r jeu égal , doivent être dans cette
proportion.
On trouveroit de même que celui qui parieroit
d’amener trois fois de fuite croix, par exemple,
auroit feulement pour lui une feule des huit
combinaifons de croix ou pile qui peuvent réfulter
| de trois jets fucceflifs de la même pièce. La pro-
! habilité de cet événement feroit conféquemment
pendant que celle qu’auroit fon adverfaire feroit
2 . Il ne devroit, pour jouer au pair , mettre
au jeu que 1 contre 7.
Il eft inutile de parcourir d’autres cas : il eft aife
de voir que la probabilité d’amener croix quatre
fois de fuite, e f t ; cinq fois de fuite, ^ ; &c.
Il n’eft pas, au refté, néceffaire d’ entrer dans
l’énumération des différentes combinaifons réful-
tantes des croix ou pile ; mais l’on peut fe fervir
d’une régie ai fée à démontrer, & que voici :
Connoijfant les probabilités-de deux ou plufeurs
événemens ifolês , la probabilité qu ils auront lieu
tous enf mble fe trouve tout fimplement , en multipliant
les probabilités de ces événemens confdercs
comme ifolês. Ainfi la probabilité d’amener croix
confîdéré comme ilolé étant exprimée à chaque jet
par celle de l’amener deux fois de fuite fera- X \ ,
o u f ; celle de l’amener trois fois dans trois coups
confécutifs fera f x £ x | , ou f ; &c.
2°. Le problème de déterminer quelle eft la
probabilité d’amèner, avec deux , trois , quatre
pièces,, tout croix ou tout pile 3 fe réfout par lés
mêmes voies. Dans deux pièce-s jettéés, il y a a
combinaifons de croix & p ile , dont une feule eu
toute croix : dans trois pièces jettées à la fois il y
en a 8 , dont une feule donne toute croix-; &c.
Ainfi les probabilités de chacun de ces Cas font les
mêmes que celles des cas analogues examines ci*
deffus,
Il paroît même d’abord fans anâiyfe que ces
deux queftions font abfolument les mêmes ; &
voici le raifonnement qu’on peut faire pour le
prouver. Jetter les deux pièces A & B ehfemble,
ou les jetter l’une après 1 autrë après avoir donné
à la première A le temps de fe fixer, c’ eft ilfinement
la même chofé. Suppofons donc que , la
première A étant fixée, au lieu de jetter la feconae
B , on relève la première A pour la jèttèr une fécondé
fois ; ce fera la même chofe que fi , pour
ce fécond j e t , on avoit employé la-pièce B:
c a r , par la fuppqfition , elles font toutes deux
égales & femblables, du moins quant à l’ indih
férence parfaite qu’il arriye croix ou pile. Ainfi
jetter à la- fois les deux .pièces A ,; B , ou jetter
deux fois de fuite la piècè A j font la memë chofe-
Donc, Ôcc.
30. On demande maintenant combien on p°ut
parier d’amener au moins une fois croix en deux
coups? Pau la méthode ci-defius, on trouvera qu’ il
y a 5 contre un. En effetS il y a dans deux coups
quatre combinaisons 3 dont trois donnent- au-moins
une fois croix dans les deux coups } Byunë feule
qui donne toujours pile ; d’ ou il fuitqu il y a trois
combinaifons en faveur de celui qui parie d’amener
une fois croix en deux coups., &: une feule
-contre lui.
P r o b l è m e I I .
Un nombre quelconque de dés étant donné , déterminer
quelle probabilité i l y a quon amènera un nom- 1
, jA-f dè points ajfgné. ...
Nous fuppoferons d'abord des dés ordinaires,
c’ eft-à-dire a fix faces y & marqués des nombres.
1 , 2 , 3 ,4 , 5 j 6 ; nous allons analyfer quel-,
ques-uns <iespremiers cas du problème, pour nous;
elever pat degré a des cas plus compofes.
1° . On pçopofe, d'amener un point détermine ,6 ;
par exemple , avec un de.
Il eft évident qu’y ayant au dé fix faces dont
une feule eft marquée de 6 & chacune ayant
autant de facilité à fe trouver en deffus qu’aucune
autre , il y a 5 hazards contre celui qui propofe
d’amener 6 en un coup , &m feul pour lui. Il doit
donc, pour n’être pas dupe, parier feulement 1
contre y.
ijj. Qu’i l foit'propofé d'amener le même point 6
avec deux dés.
Pour analyfer ce cas , il faut d’abord obferver
que deux dés donnent 3 G combinaifons différentes;
car chacune des faces du dé A , par exemple
, peut fe combiner avec chacune de celles du
dé B ; ce qui produit 36 combinaifons. 11 -faut
énfuite voir de combien de manières le point 6
peut être amenêavec deux dés. Or on trouve qu’il
peut être d’abord amené par 3 &: 3 : 2° en amenant
2 avec le dé A & 4 avec le de B , ou 4 avec
le dé A & 2 avec le dé B ; ce qui fa it, comme il
eft aifé de v oir , deux cas diftinéls : 30 en amenant
1 du dé A & y du dé B , ou 1 du dé B & 5
du dé; A;; ce qui donne encore deux cas : on n’en
fauroit évidemment trouver d’autres. Ainfi il y a
î cas favorables fur 36 : conféquemment la probabilité
d’amener 6 avec deux dés eft & la
probabilité de ne le pas amener eft § f ; & c’eft le
rapport dans lequel doivent être les mifes des
joueurs.
En analyfant les autres cas , on trouve qu’ il y
a , pour amener detix avec deux dès , 1 cas fur
• 36 , 2 poiir amener trois, 3 pour amener quatre,
4 pour amener c in q , c pour amener fix , 6 pour
'.amener fept, 5 pour nuit, 4 pour neuf, 3 pour
.dix, 2 pour onze, & 1 pour douze ou fonnez.
, l otI propofoit trois dés, avec lefquels il eft
évident que le moindre point feroit trois , & le
plus grand dix-huit , on trouveroit, au moyen
dJune femblable analyfe, que fur 116 coups diffé--
rens poffibles avec trois dés, il y en a 1 pour
amener trois, 3 pour amener quatre, <5 pour amener
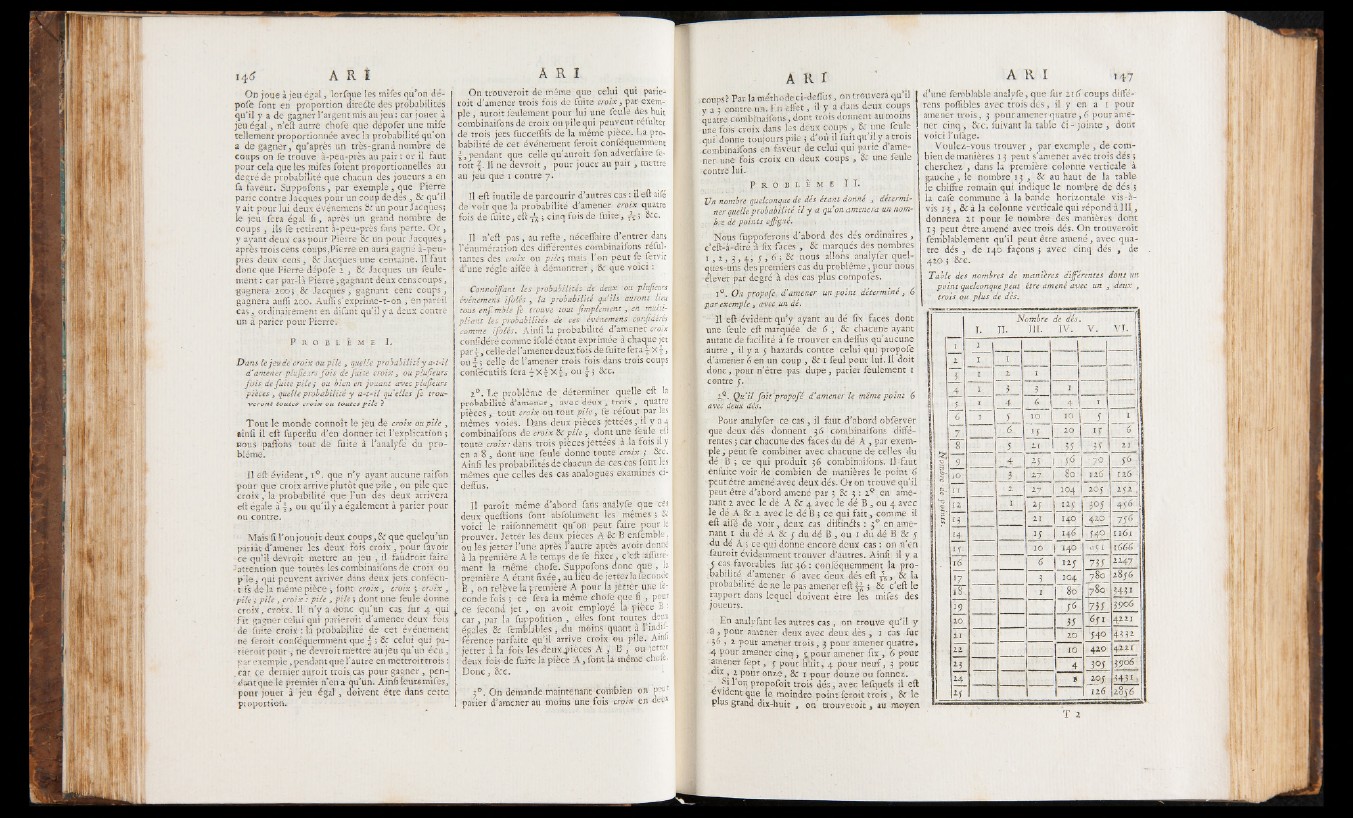
cinq , & c . (uivant la table ci - jointe , dont
voici l ’ufage.
Voulez-vous trouver , par exemple , de combien
de manières 13 peut s’amener avec trois dés ;
cherchez , dans la première colonne verticale à.
gauche , le nombre. 13 , & au haut de la table
le chiffre romain qui indique le nombre de dés';
la café commune à la bande horizontale vis-à-
vis 13 , & à la colonne verticale qui répondâ. I l f ,
donnera 21 pour le nombre des manières dont
13 peut être amené avec trois dés. On trouveroit
femblablement qu’ il peut être amené, avec quatre
dés , de 140 façons ; avec cinq dés , de
410 ; &c.
Table des nombres de manières différentes dont un
point quelconque peut être amené avec un , deux ,
, ^ trois o,u plus de dés.
I.
Nombre
n. m.
de dés.
IV. V." VI. "J
1 I 1
2 I 1 |
3 I 2 I j
.4 I , y . " 3 I j
? I 4 6: 4 1 i l
6 I s IO J 10 ! 3 ' ï
7 13 20 - 13 6
8 î XI ’ - 33 ‘33 ! 21
? 9 4 Xî 33ËR .70 1 1
Cr- IO § 27 .80 12<J- I26
A i l > xÿi,® 10 4 . x p ;
•V C 12 1 -m 4 3 â :
» 21 140 4x0 736 :
H 146, -3 4 9 : I l 61
l S IO 140 [jjjjÉ 1666 •
16 6 • 733 iX47
l 7 3 104. 780 2856
18 I 801 (780 3431
19
G\
b ?3 3906
20 33 ' f ; i 422 ï
21 | 20 ■ 340 4 3 3X
22 10 420 4221
*3 4 3°3 3906
H t X03 343 1 !
. !2 6 x8jé
T z