47® A D H
Donc fi on appelle P la force avec laquelle adhère
à l’eau un difque de verre dont le diamètre eft a ,
& y l a force d’adhéfion d’un difque de même matière
dont le diamètre eft bt on aura la proportion,
a 1 : b ’ p : y ; & y = L jE
Pour vérifier la régularité de cette progreffion,
foit avec l’eau, foit avec d’autres fluides, M. Achard
a employé des difques de verre de glace depuis i {
A D H
pouce jufqu’à t' pouces de diamètre , il a d’abord dé-;
terminé leur force d’adhéfion avec ces fluides par la
fomme des grains qui ont été néceflàires pour la vaincre
; il l’a enfuite cherchée par l’équation ci-deffus.
La table fuivante, où fe trouvent rapprochés les*
réfultats de l’obfervation & du calcul, lui ont démontré
qu’il n’y avoit que de très-foibles différences
& telles qu’elles procèdent toujours néceffairemeot
des matières & des inftrumens.
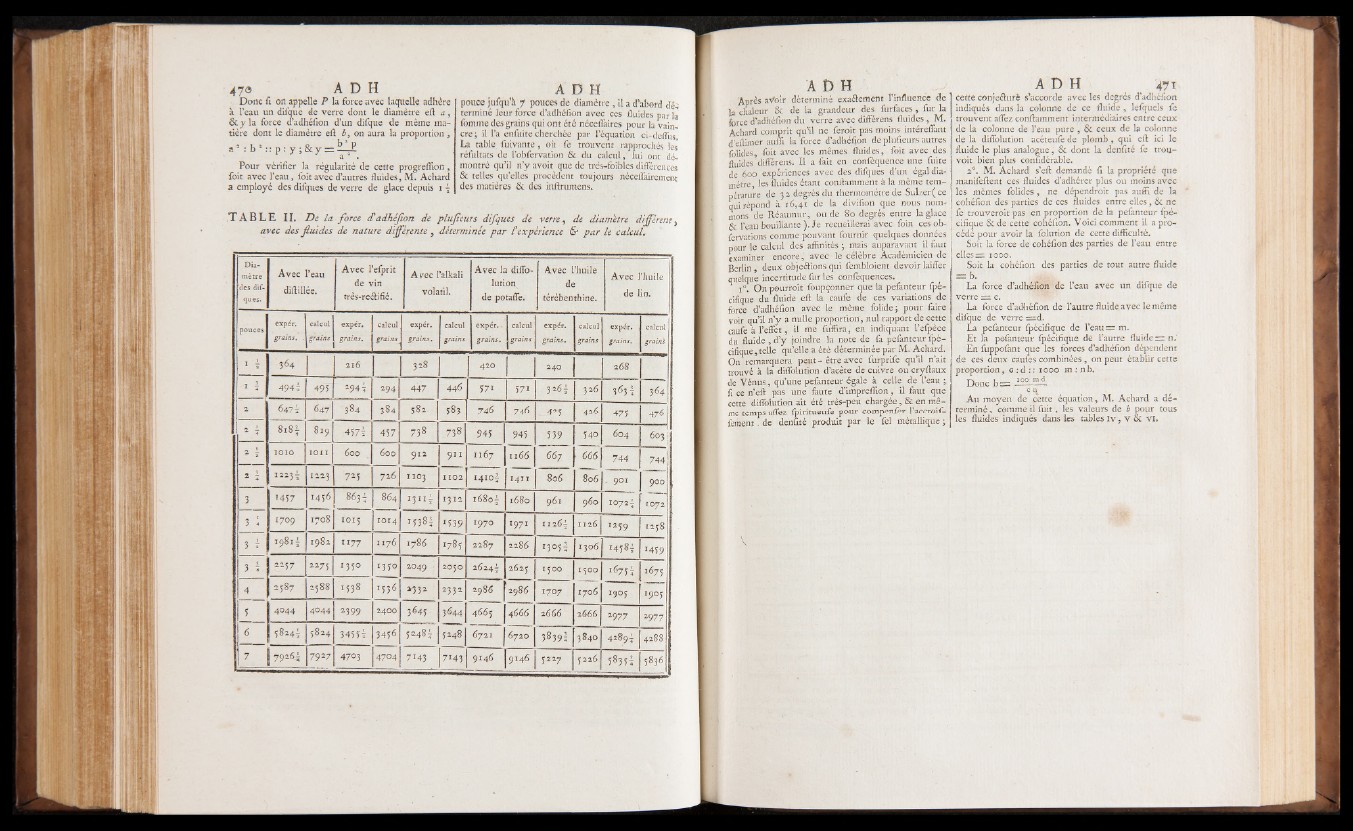
T A B L E I I . D e la force etadhéjion de plujîeurs difques de verre 9 de diamètre différent}
avec des fluid e s de nature différente 9 déterminée par £ expérience & par le calcul.
Diamètre
des difques.
Avec l’eau
diftillée.
Avec l’efprit
de vin
. très-re&ifié.
A vec l’alkali
volatil.
Avec la diffolution
de potafle.
Avec l’huile
de
térébenthine.
Avec l’huile
de lin.
pouces
expér. calcul expér. calcul expér. calcul expér.. calcul expér. calcul expér. calcul
grains. . grains grains. grains grains. grains grains. I grains grains. grains grains. graini
1 T 364 216 328 420 240 268
•I 1 494 i 495 294ï 294 447 446 371 571 3 26 T 32 6 363 4 364
2 6474 647 384 384 582. 583 746 746 . 425 426 475 476
2 \ . 818J 819 1 457; 457 738 738 945 945 539 540 604 603 i
2 j IOIO IOII 600 600 912 911 1167 i i 66 667 666 744 744
2 | I223 i 1223 725 726 1 103 1 102 I4I0J 1411 806 8p6 , 901 900
3 »457 1456 8634 864 I3r I ; I312 1680-J 1680 961 960 IO7 2- 1072
3 4 1709 1708 iOIJ IOI4 i 538ï M39 1970 1971 1126^ 1126 1239 1258
3 i 19$I± 1982 1177 II76 1786 1785 2287 2286 . 13054 1306 14584 '459
3 x 2257 2275 1350 ! 35° 2049 ■ 2050 26 24-J 2625 1500 1 s ° ° i6754 ,1675
4 2587 2588 1538 1536 2^32 2332 29 86 2986 1707 1706 1905 1905
î 4044 4°44 *3 99 2400 3645. 3^44 j 4665 4666 2666 2 666 2977 2977
1! 6
5824!
•
5824 3W ; 3456 52484 5248] 6721 67 20 38394 3840 42892 4288
I7 79264 7927 4703 4704 7M3 p | J 9M6 9146 5227 5226 58354 5836
A D H
Après aVoir déterminé exaâement l’influence de
la chaleur & de la grandeur des furfaces , fur la
force d’adhéfion du verre avec différens fluides, M.
Achard comprit qu'il ne ferait pas moins intéreffant
d’eftimer aufli la force d’adhéfion de plufieurs autres
folidesj foit avec les mêmes fluides, foit avec.des
fluides différens. Il a fait en conféquénce une fuite
de 606 expériences avec des difques d’un égal diamètre,
les fluides étant conflamment à la même température
de 32 degrés du thermomètre de Sulzer(ce
qui répond à 16,41 de la divifion que nous nommons
de Réamnur, ou de 80 degrés entre la glace
& l’eau bouillante ). Je recueillerai avec foin cesob-
fervations comme pouvant fournir quelques données
pour le calcul des affinités ; mais auparavant il faut
examiner encore I avec le célèbre Académicien de
Berlin , deux objections qui fembloient devoir laiffer
quelque incertitude fur les conféquences.
i°. On pourrait foupçonner que la pefànteur fpé-
cifique du fluide eft la caufe de ces variations de
force d’adhèfion avec le même folide; pour faire
voir qu’il n’y a nulle,proportion, nul rapport de cette
caufe à l’effet, il me fuffira, en indiquant l’efpèce
du fluide , d’y joindre la note de fa pefànteur fpé-
cifique, telle qu’elle a été déterminée par M. Achard.
On remarquera peut - être avec furprife qu’il n’ait
trouvé à la diffolution d’acète de cuivre ou cryftaux
de Vénus, qu’une pefànteur égale à celle de l’eau ;
fi ce n’eft pas une foute d’impreflion, il faut que
cette diffolution ait été très-peu chargée, & en même
temps affez fpiritueufe pour compenfer l’accroif-
fement. de denfité produit par le fel métallique ;
ADH ■ . m cette conje&urè s’accorde avec les degrés d’adhéfion
indiqués dans la colonne de ce fluide, lefijuels fe
trouvent affez conftamment intermédiaires entre ceux
de la colonne de l’eau pure , & ceux de la colonne
de la diffolution acéteufe de plomb, qui eft ici le
fluide le plus analogue | & dont la denfité fe trou-
voit bien plus considérable.
2°. M. Achard s’eft demandé fi la propriété que
manifeftent ces fluides d’adhérer plus ou moins avec
les mêmes folides, ne dépendroit pas aufli de la
cohéfion des parties de ces fluides entre elles, & ne
fe trouveroit pas en proportion de la pefànteur fpé-
{ cifique & de cette cohéfion. Y oici comment il a pro-
] cédé pour avoir la folution de cette difficulté.
Soit la force de cohéfion des parties de l’eau entre
elles = 1000.
Soit la cohéfion des parties de tout autre fluide
La force d’adhéfion de l’eau avec un difque de
verre c.
La force d’adhéfion de l’autre fluide avec le même
difque de verre = d .
La pefànteur fpécifique de l’eau = m.
Et la pefànteur fpécifique de l’autre fluide n.
En fuppofant que les forces d’adhéfion dépendent
de ces deux caules combinées, on peut établir cette
proportion, c : d : : 1000 m : nb.
Donc b = ■
c n
Au moyen de çette équation, M. Achard a déterminé
, comme il fuit, les valeurs de b pour tous
les fluides indiqués dans les tables i v , V & VI.
H