I
i l l l
Garantie, daß jedes $ wirksam, befruchtet wird, sicher größer als bei den Kugeln mit hohen Jungenzahlen.
Die angegebene Zahl von 25—30 ? für ein <$ ist ja eine Durchschnittszahl, die wohl häufig
überschritten wird. Sicher gibt es aber auch Fälle, wo die c? nur weniger $ befruchten können. Ich
glaube in der Tat, daß auch Fälle Vorkommen, wo das <? sexuell überbeansprucht wird, und die Befruchtung
eines $ nicht ausreichend ist. Ich verweise hier auf Versuch XV25 in Tabelle 2. Hier h a tt
eine Kugel von 1044 [i Durchmesser 159 Jungmilben. Davon waren 88 <$ und nur 71 ?. Eigenartig
ist, daß die ? nur in den 5 ersten Tagen geboren wurden, am 10. und 11. Tage folgten noch einmal
6 und 1 Die später geborenen Tiere waren alle <?. Dieser Versuch läßt sich vielleicht so erklären,
daß die bei der Kopulation erhaltene Spermamasse für die Befruchtung aller Eier dieses ? nicht ausreichte,
und daß hauptsächlich die ersten reifen Eier befruchtet werden konnten, die späteren sich
aber unbefruchtet entwickeln mußten. Wahrscheinlich war das <? hier sexueE ziemlich erschöpft.
Auch W i l d e r m o u t h (nach W e b s t e r , 1910) scheint ähnliche Fälle beobachtet zu haben.
In einem Versuch wurden von einem? 26c? geboren, in einem ändern Versuch eine große Zahl (,,a large
number“). Eine Erklärung hierfür wird allerdings nicht gegeben. Die Fälle sind nur angeführt als
Ausnahme von dem gewöhnlichen Durchschnitt, wo 3—8 <? von einem $ geboren werden.
Tabelle 11.
Kugelgröße
in u
II
Durchschnittszahl
der von einem <?
begatteten $ '
Kugelgröße
in u
Durchschnittszahl
der von einem <?
begatteten
x x v 25 . . . . m ■ - 937 • 61,7 Z XII . . . . . . . . 1075 . 55,8
VII25 . . . . 43 Z Y I I ........................... 1Ó55 48,6
XXIV25 . . . . . . . 980 39,3 . Z X IV ........................... . 103.2 , ; 43,7
XXIIIgg . . . . . . . 895 * US, 5 Z X V I......................................... 903 43
XVI25 . . . . . . . 948 38,3 Z V I I I......................................... 833 42 .
XIII* . .. . . . . .. 916 37,5 ZV ........................... 989 39,3
III25 . . . 36,8 Z X I I I......................................... 925 37,3
V<* . . . .l | B | i | 916 35,3 Z XI ........................... 774 34,8
XI.* . . . . . . 575 31 Z VI ......................................... 989 33,6
1X35 . . . . , . 809 ' 28,6 ZI ......................................... 720 .26,8
II25 . . . . . . | 1012 26 ZX ........................... 5591 24,1
XXII25 . . . . . . 852 26 ZIII ......................................... 903 19
IV* . . • M H ! 1001 25,4 ZIV ......................................... 860 . 15,7
XVIIL* . . . . . . 873 23 Z XV ........................... 957 15,3
Xllj* . . . . 19,1 z u ......................................... 620 11
XIV.* . . . 852 18,6 ZIX ........................... 538 9
125 . . . • . . . 863 18
x 25 . . . . . . 895 15,9
VIII25 . . . . . . 927 .15,8
XX25 . . . . . . 994 13,2
XXL* . . . . . . 1012 12,4
XIX25 . . . .... 628 10
XVIL* . . . .... 767 4,5
In diesem Zusammenhang gewinnt auch die Frage an Interesse, welche Gesetzmäßigkeiten
wohl vorwalten mögen in dem Auftreten der <? bei befruchteten Kugeln. Denn daß gewisse Gesetzmäßigkeiten
vorliegen, ist mir durchaus wahrscheinlich, da, wie wir ja schon sahen, das erste <? fast
regelmäßig. am 1. Tag der Geburtsperiode, meist sogar als 1. Tier geboren wird (siehe Tabelle 2, 3
und 12). Ja , auch für das an 2. und 3. Stelle geborene <? läßt sich noch eine gewisse Regelmäßigkeit
im Auftreten nachweisen. Für die weiteren <? verwischt sich diese Regelmäßigkeit des Auftretens
immer mehr.
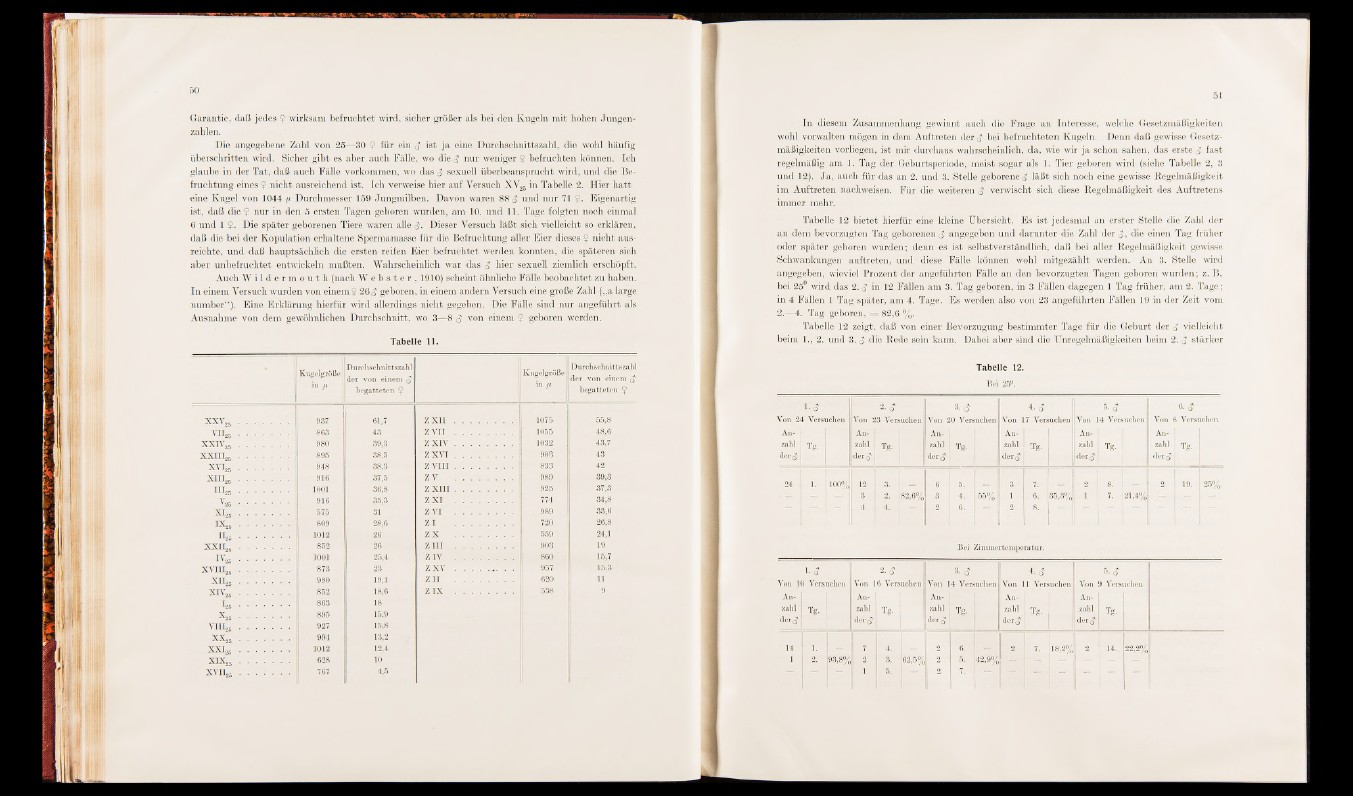
Tabelle 12 bietet hierfür eine kleine Übersicht. Es ist jedesmal an erster Stelle die Zahl der
an dem bevorzugten Tag geborenen <$ angegeben und darunter die Zahl der <?, die einen Tag früher
oder später geboren wurden; denn es ist selbstverständlich, daß bei aller Regelmäßigkeit gewisse
Schwankungen auf treten, und diese Fälle können wohl mitgezählt werden. An 3. Stelle wird
angegeben, wieviel Prozent der angeführten Fälle an den bevorzugten Tagen geboren wurden; z. B.
bei 25 wird das 2. c? in 12 Fällen am 3. Tag geboren, in 3 Fällen dagegen 1 Tag früher, am 2. Tage;
in 4 Fällen 1 Tag später, am 4. Tage. Es werden also von 23 angeführten Fällen 19 in der Zeit vom
2.—4. Tag geboren, — 82,6 %.
Tabelle 12 zeigt, daß von einer Bevorzugung bestimmter Tage für die Geburt der <? vielleicht
beim 1., 2. und 3. <$ die Rede sein kann. Dabei aber sind die Unregelmäßigkeiten beim 2. c? stärker
Tabelle 12.
Bei 25°.
l - ' c ? 2. :? 4- <? 5. <? -e. s -
Von 24 Versuchen Von 23 Versuchen Von 20 Versuchen Von 17 Versuchen Von .4 Versuchen Von 8 Versuchen
An- I An- I An- I An- I AnAn
[
zahl Tg. zahl Ter zahl rg. zahl 1 Tg. zahl Tg. zahl 1 Tg.
der<? . derr? der<? derc? 1.
24 1. 100%
1
12 3 6 5.
■ n s
3 i 7. 2 8. — 2 19. 25%
3 2 ,3 4. 1 6. 35,3% 1 7. \n ,i%
4 4. 2 6.
■ 1
Bei Zimmertemperatur.
2- 0 4. $ 5 . (?
Von 16 Versuchen Von 16 Versuchen Von 14 Versuchen Von 11 Versuchen Von Versuchen
AnAnAnAn
I Anzahl
Tg. zahl Tg. zahl’ Tg. zaH Tg. zahl Tgder
«? der<J der(? der £
14 1. » 4. 1 2;'" 6. . — ' [ 7. lS Ä 14., M
22 1 •2.'' 93,8%m H 3. 62,5%r-1 5. 42,9% _ j _ 5. \ j,
^