Au-dessous de l’isobathe 300™
VOLUME DU LAG
368 millions
TEMPÉRATURE
5.0°
entre 250m et 300 3901 — 5.0
— 200 250 7567 — 5.1
— 150 200 10785 — 5.2
—. 100 150 13875 — 5.4
Soit un volume total, au-dessous de l’isobathe de 100m, de 36 496 millions
de mètres cubes, ayant emmagasiné une quantité de 190 944 milliards
de calories au-dessus de 0°.
Si nous mélangeons ces deux masses d’eau, nous obtenons une température
moyenne de 5.59°, soit 5.6°.
Par conséquent, par le fait seul de l’entrée de l’eau du Rhône et de
sa descente dans les profondeurs du lac, pendant l’été de 1886, la
température des couches profondes se serait réchauffée de 0,6°, en
passant de 5.0° à 5.6°. Ce calcul nous montre que malgré son apparence
paradoxale, la formule est exacte, qui dit : Le Rhône, fleuve-
g la c ia ire , ré c h a u ffe le s c o u c h e s p ro fo n d e s du Léman. Cette
formule est exacte ; car c’est parce qu’il est fleuve glaciaire, que le
Rhône est chargé de limon et amène en été ses grandes eaux qui
sont plus lourdes que celles du lac. Il réchauffe le lac parce que, alors
même qu’il est un fleuve glaciaire, ses eaux d’été se sont assez réchauffées
dans la traversée du Valais pour être plus chaudes que les eaux
profondes du Léman, avec lesquelles elles vont se trouver en contact.
Une seule chose doit nous étonner, c’est la valeur considérable de
l’élévation de température que nous indique ce calcul : 0.6» c’est beaucoup
plus que le taux normal du réchauffement que nous ont montré
les sondages thermométriques; ceux-ci nous ont donné pour l’élévation
de température des couches profondes d’une année à l’autre 0.1, ou 0.2,
ou au plus 0.3°. Il doit donc y avoir, pour contrebalancer le puissant,
réchauffement de la convection hydrostatique, une cause de refroidissement
que nous avons jusqu’à présent négligée. Nous la'trouverons
plus loin lorsque nous étudierons le refroidissement de la région littorale
en hiver.
III. VARIATION JOURNALIÈRE
Nous avons vu que la surface du lac varie de température dans la
période journalière ; la variation du lac est plus faible que celle de la
température atmosphérique, mais elle s’élève encore dans les mois
d’été à 2° environ, et elle peut atteindre 4° dans des cas exceptionnels.
Cette variation se fait-elle sentir dans les couches sous-jacentes ?
Jusqu’à quelle profondeur se fait-elle sentir ? Comment la variation se
traduit-elle dans les courbes thermiques ?
Supposons que la périodicité journalière n’existe pas encore dans
les actions thermiques qui opèrent sur le lac; supposons que, les
vingt-quatre heures durant, comme cela a lieu au pôle èn été, le soleil
réchauffe constamment la surface de l’eau, sans variation sensible
dans l’intensité de l’action. Dans ce cas la chaleur irait régulièrement
et progressivement en croissant ( ’) dans les couches de plus en plus
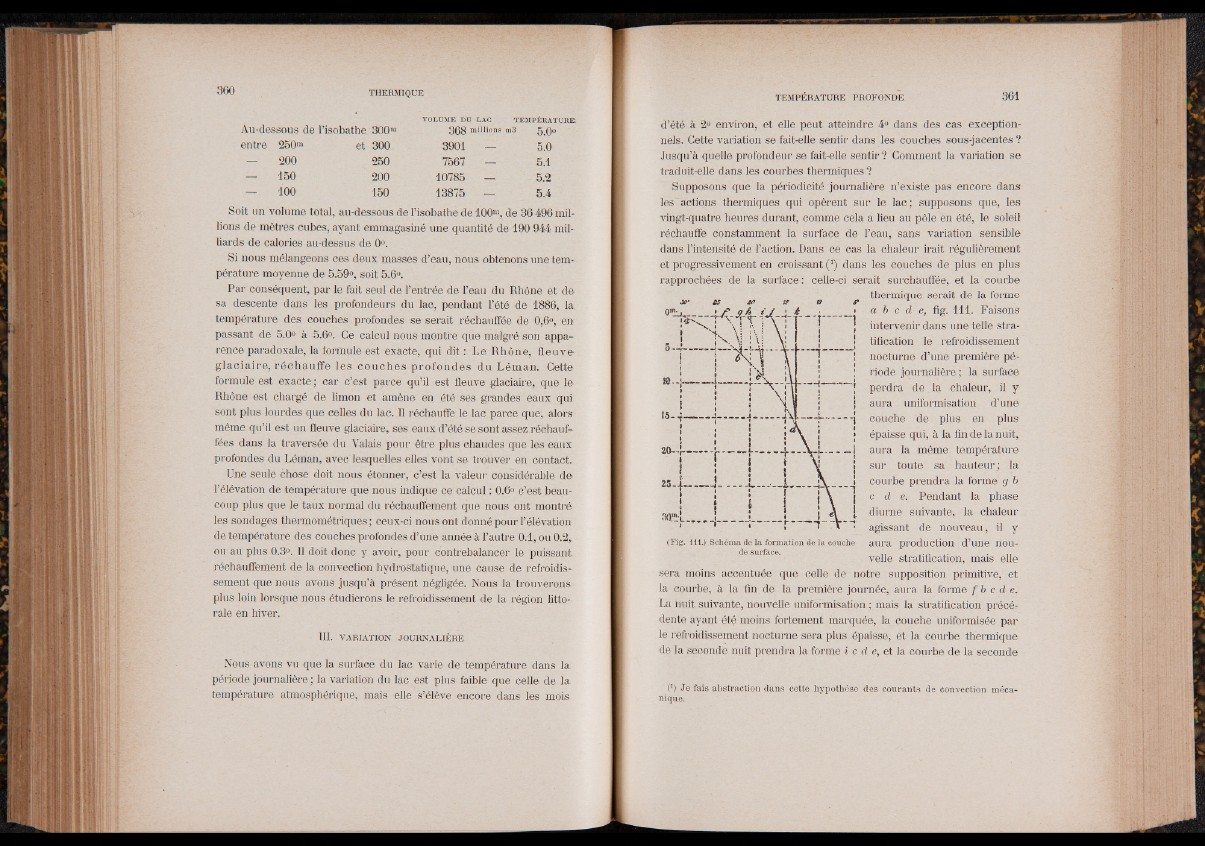
rapprochées de la surface: celle-ci serait surchauffée, et la courbe
thermique .»>- si to tr a serait de la forme
a b c d e, fig. 111. Faisons
intervenir dans une telle stratification
le refroidissement
nocturne d’une première période
journalière; la surface
perdra de la chaleur, il y
aura uniformisation d’une
couche de plus en plus
épaisse qui, à la fin de la nuit,
aura la même température
sur toute sa hauteur ; la
courbe prendra la formé g b
c d e. Pendant la phase
diurne suivante, la chaleur
agissant de nouveau, il y
aura production d’une nouvelle
stratification, mais elle
(Fig. 111.) Schéma de la formation de la couche
de surface.
sera moins accentuée que celle de notre supposition primitive, et
la courbe, à la fin de la première journée, aura la forme f b c d e .
La nuit suivante, nouvelle uniformisation ; mais la stratification précédente
ayant été moins fortement marquée, la couche uniformisée par
le refroidissement nocturne sera plus épaisse, et la courbe thermique
de la seconde nuit prendra la forme i c d e, et la courbe de la seconde
C) Je fais abstraction dans cette hypothèse des courants de convection mécanique.