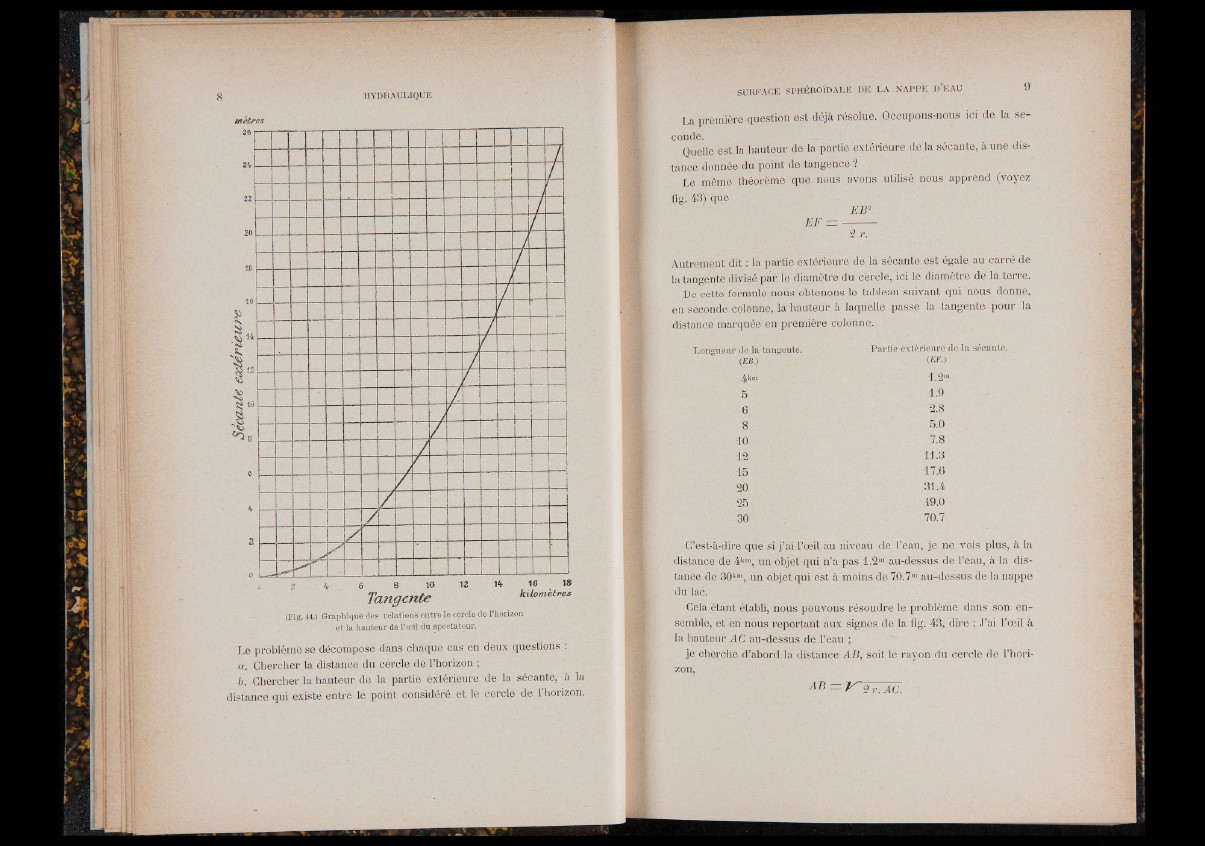
mètres
(Fig. 44.) Graphique des relations, entre le cercle de l’horizon
et la hauteur de l’oeil du spectateur.
Le problème se décompose dans chaque cas en deux questions :
a. Chercher la distance du cercle de l’horizon ;
b. Chercher la hauteur de la partie extérieure de la sécante, à la
distance qui existe entre le point considéré et le cercle de l’horizon.
La première question est déjà résolue. Occupons-nous ici de la seconde.
—.
Quelle est la hauteur de la partie extérieure de la sécante, à une distance
donnée du point de tangence ?
Le-même théorème que nous avons utilisé nous apprend (voyez
fig. 43) que
E B 2
E F — ---------
•2 P
Autrement dit : la partie extérieure de la séèante est égale, au carré de
la tangente divisé par le diamètre du cercle, ici le diamètre de la terre.
De cette formule nous obtenons le tableau suivant qui nous donne,
en seconde colonne, la hauteur à laquelle passe la tangente pour la
distance marquée en première colonne.
Longueur de la tangente. Partie extérieure de la sécante.
(EB.) (EF.)
4km 1 .2m
5 1.9
6 2.8
8 5.0
10 7.8
12 1 1.3
15 1 7 .6
20 31.4
25 49.0
30 70.7
C’est-à-dire que si j’ai l’oeil au niveau de l’eau, je ne vois plus, à la
distance de 4km, un objet qui n’a pas 1.2m au-dessus de l’eau, à la distance
de 30km, un objet qui est à moins de 70.7m au-dessus de la nappe
du lac.
Cela étant établi, nous pouvons résoudre le problème dans son ensemble,
et en nous reportant aux signes de la fig. 43, dire : J’ai l’oeil à
la hauteur AC au-dessus de l ’eau ;
je cherche d’abord la distance AB, soit le rayon du cercle de l’horizon,
AB — W3 B