148 PHI LO SO PHI S E N A T U R A L I S
vallo C A defcribatur globus exterior PDAF, & intra hunc globum.
a rota, cujus diameter fit AO, defcribantur du® femicycloides AQ,
A S , qu® globum interiorem tangant in £ & S & globo, exterior!
occurrant in A. A pun&o ilio A, filo A P T longitudinem A R
*quante, pendeat corpus T, & ita intra femicycloides A S ofcilletur,
ut quoties pendulum digreditur a perpendículo A R , filum
parte fui fuperiore A P applicetur ad femicycloidem illam APS:
verfus quam peragitur motus, & circum earn ceu obfiaculum flefla-
tur, parteque reliqua P T cui femicyclois nondum objìcitur, pro-
tendatur in lineam re&am ; & pondus T ofcillabitur in cycloide data
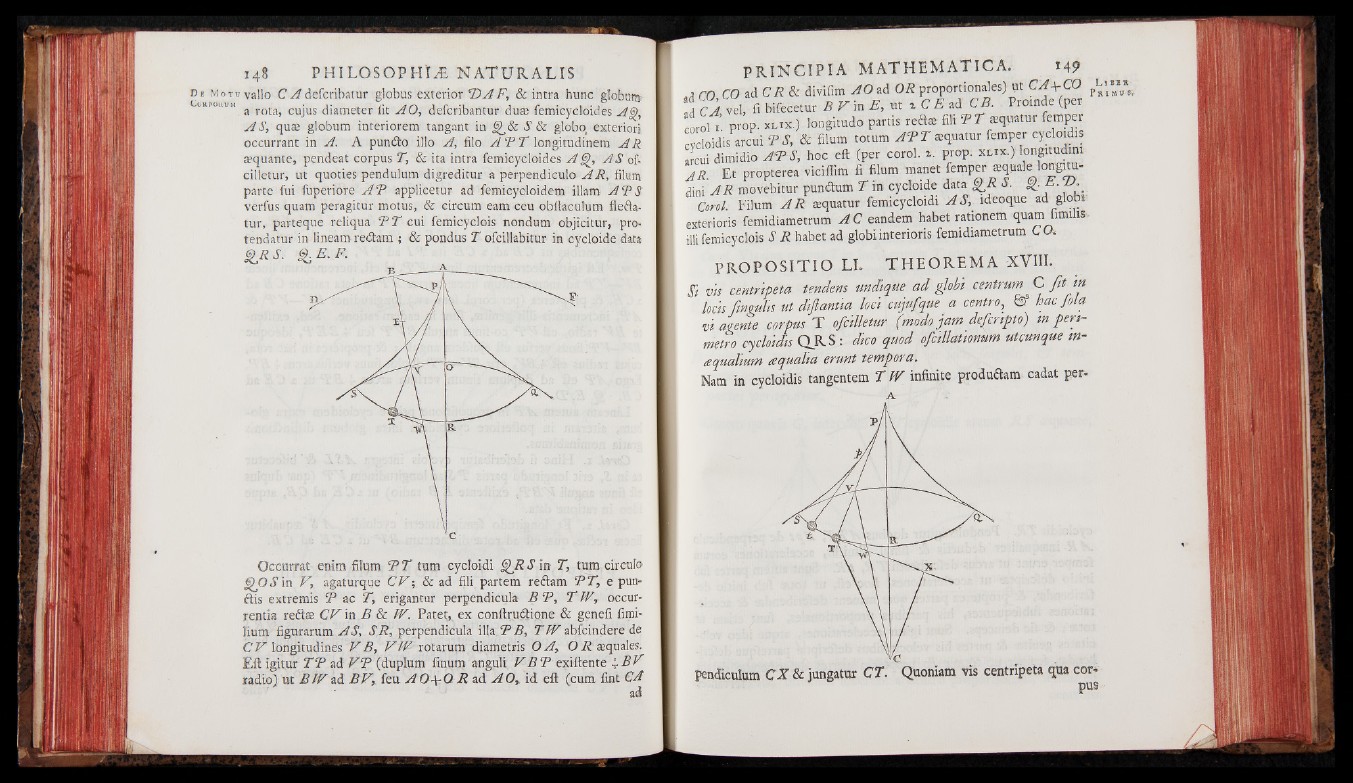
Occurrat enim filum P T tum cycloidi £22 S in T, tum circulo'
9 0 S in V, agaturque CV-, & ad fili partem reftam P T , e pun-
ftis extremis P ac T, erigantur perpendicula B P , T W, occur-
rentia reft® C V in B & W. Patet, ex conftru&ione & genefi fimi-
fium figurarum AS, SR, perpendicula illa P B, TW abfcindere de
C V lbngitudines V B , V IV rotarutn diametris 0 A,. O R «quales.
Eft igitur T P ad V P (duplum finum anguli V B P emittente 4.B V
radio) ut B W ad B V , feu A O \ - 0 R ad A O , idi eft (cura lint CA
P R I N C I P I A M A T H E M A T I C A . 149
A CO CO ad CR & divifim A O ad OR proportionales) ut CA+CO
d C A vel, fi bifecetur B V in E, ut * C E ad CB. Proinde (per Wm B Mi M M r e a * KB lil
rveloidis arcui P S , & filum totum A P T «quatur femper cycloidis
arcui dimidio A P S, hoc eft (per corol. i prop. x l i x .) longitudini
AR Et propterea vicifiim fi filum manet femper «quale longira-
dini A R movebitur punftum T in cycloide data £22 S. £ . M K
Corol. Filum A R ®quatur femicycloidi A S , ìdeoque ad globi
exterioris femidiametrum A C eandem habet rationem quarn fimilis
illi femicyclois £ 22 habet ad globiinterioris femidiametrum CO.
P R O P O S I T I O L L T H E O R E M A XVIII.
Si vis centripeta tendens unitane ad globi centrum C f i t in
locis finmlis ut diflantia loci cujufque a centro, & hac fola
vi agente corpus T ofcilletur (modo jam dejcripto) m perimetro
cycloidis Q R S : dtco Vuod °fiillationum utcunque tn-
aquahum aqualia erunt tempora.
Nam in cycloidis tangentem T IV infinite produftam cadat p e *
A
pendiculum C X & iungatur CT. Quoniam vis centripeta qua corpus