c/JÌfÌÌ G L 0 K 'm infinitum verfus O K produda. Sed area ilia (per notas
quadraturarum methodos) eft reciproce ut C G ~ 3, & propterea vis
folidi totius eft reciproce ut CG"~3. 61 E. D .
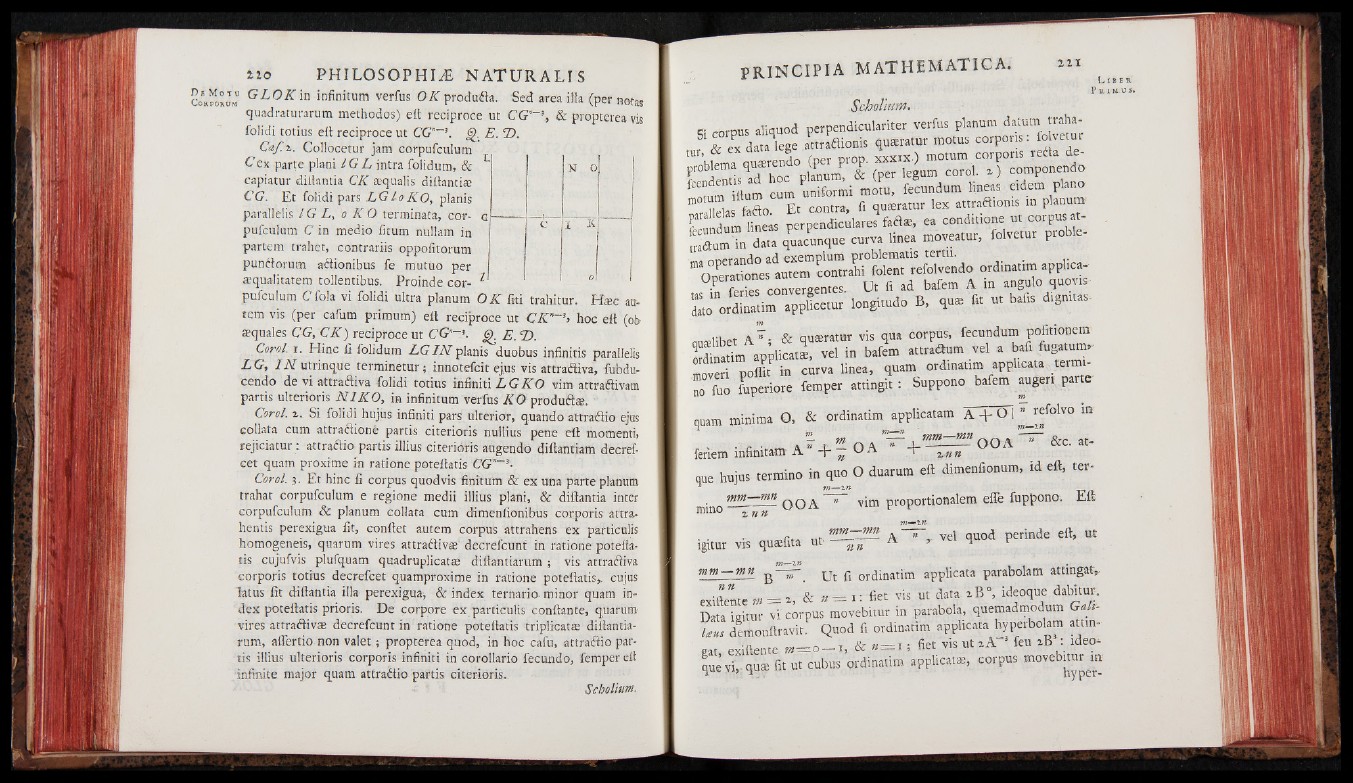
Caf.%. Collocetur jam corpufculum
C ex parte plani IG L intra folidum, &
capiatur difiantia CK equalis diitantiae
CG. Et folidi pars L G lo KO, planis
parallelis IG L, o K O terminata, corpufculum
C in medio fitum nullam in
partem trahet, contrariis oppofitorum
pundorum aciionibus fe mutuo per
aequalitatem tollentibus. Proinde corpufculum
C fola vi folidi ultra planum O K lìti trahitur. H e c antera
vis (per cafum primum) eft reciproce ut C K ’' - 3, hoc eft (oh
equales CG, C K ) reciproce ut CG"~k © E. T).
Corol: r. Hinc fi folidum LG IN planis duobus infinids parallelis
L G , I N utrinque terminetur; innotefcit ej,us vis attradiva, fubdu-
cendo de vi attradiva folidi totius infiniti L G K O vim attradivam
partis ulterioris N IK O , in infinitum verfus K O produd®. •
Corol. a.. Si folidi hujus infiniti pars ulterior, quando attradio ejus
collata cum attradionè partis citerioris nullius pene eft momenti,
rejiciatur : attradio partis illius citerioris augendd diftantiam decref-
cet quam proxime in ratione poteftatis CG"-'3-
Corol. 3. Et hinc fi corpus quodvis ftnitum & ex una parte planum
trahat corpufculum e regione medii illius plani, & difiantia inter
corpufculum & planum collata cum dimenfionibus corporis attra-
hentis perexigua fit, conftet autem corpus attrahetls ex particulis
homogeneis, quarum vires attradive decrefcunt in ratione potefla-
tis cujufvis plufquam quadruplicate diftantiarum ; vis attradiva
corporis totius decrefcet quamproxime in ratione poteftatis* cujus
latus fit difiantia illa perexigua; & index ternario, minor quam index
poteftatis prioris. De corpore ex particulis confiante, quaruro
vires attradivae decrefcunt in ratione poteftatis triplicate diftantiarum,
affertio non valet ; propterea quod, in hoc cafu, attradio partis
illius ulterioris corporis infiniti in corollario fecundo, femper eft
infinite major quam, attradio partis citerioris..
Scholium.
P R I N C I P I A M A T H E M A T I C A . sp$|
Scholium. I ÜH aiiquod pcrpendiculariter verfus planum datum traha-
Ü H H H H m m morns corporis : fo ve.ur
ohlema qtnerendo (per prop, r a a . ) » « H E H
w m m m H i & ^ c°ro1' 1 “ "’pone,n H H cum uniformi fecunden Snws erdem plano 1 fado. Et contra, fi queratur lex attradionis in planu
r ndnm lineas perpendiculares fade, ea conditione ut corpus at-
tradum in data (piaconquc cnrva linea moveatur, folvetur pro I
KOperatroHnes au h S h H ¡n H lo S s
B, , « 1 , « balls dignilas.
niislibet A*"; & queratur vis qua corpus, fecundum pofitionem
S p a t im applicai», vel in bafem ..tradum vei a baft fug«»m„ ■ H H curva linea, quam o rd ina™ applicata term.-
“ t o S e r io r e femper attingil : Suppone bafem auger, parte
quam minima Q, Sc ordinatim applicataci A + O i ”_ " fol,° m
Ife r.i em Imfi mHtam A H -+- n O A ^ z.nn ’r 1 c m* atque
hujus termino in quo O duarum eft dimenfionum, id eft, term—
SB T' CL
■ o O A MÈI vim proportionalem effe fuppono. Eft
mino zitti
tn—in
r mm—mn n IH qUOd perinde eft, ut
igitur vis quefita ut- ~n ^ 1 r
m—m 1 «• .
mm— mn \jt fi ordinatim applicata parabolam attingati
exilíente « 1 1 1 « | fiet vis ut data R f l ideoque dabitur.
Data igitur vi corpus movebitur in parabola, quemadmodum Gali-
B — Quod fi ordinatim applicata hyperbolam attintat
exiftente « = o - i , & B 5 fiet vis Ut lA feU B B que yi* quae fit ut cubus ordinatim applicate, corpus movebjurm