prop, xvi.) aequalis eft velocitati corporis
dimidio intervalli S T circulum
circa idem centrum J uniformiter
defcribentis. Minuatur parabolae
latitudo C T in infinitum eo,
ut arcus parabolicus T f B cum re-'
¿ta CB, centrum S cum vertice B,
& intervallum S T cum intervallo BC
coincidat, & conftabit propofitio
& E. D.
P R O P O S I T I O XXXV. T H E O R E M A XI.
Iifdempofitis, dico quod area figura D E S , radio indefinm
S D defcripta, aquahs f i t area quam corpus, radio dimì-
dium lateris retti figura D E S dquante, circa centrum S
uniformiter gyrando, eodem tempore defcribere potefi.
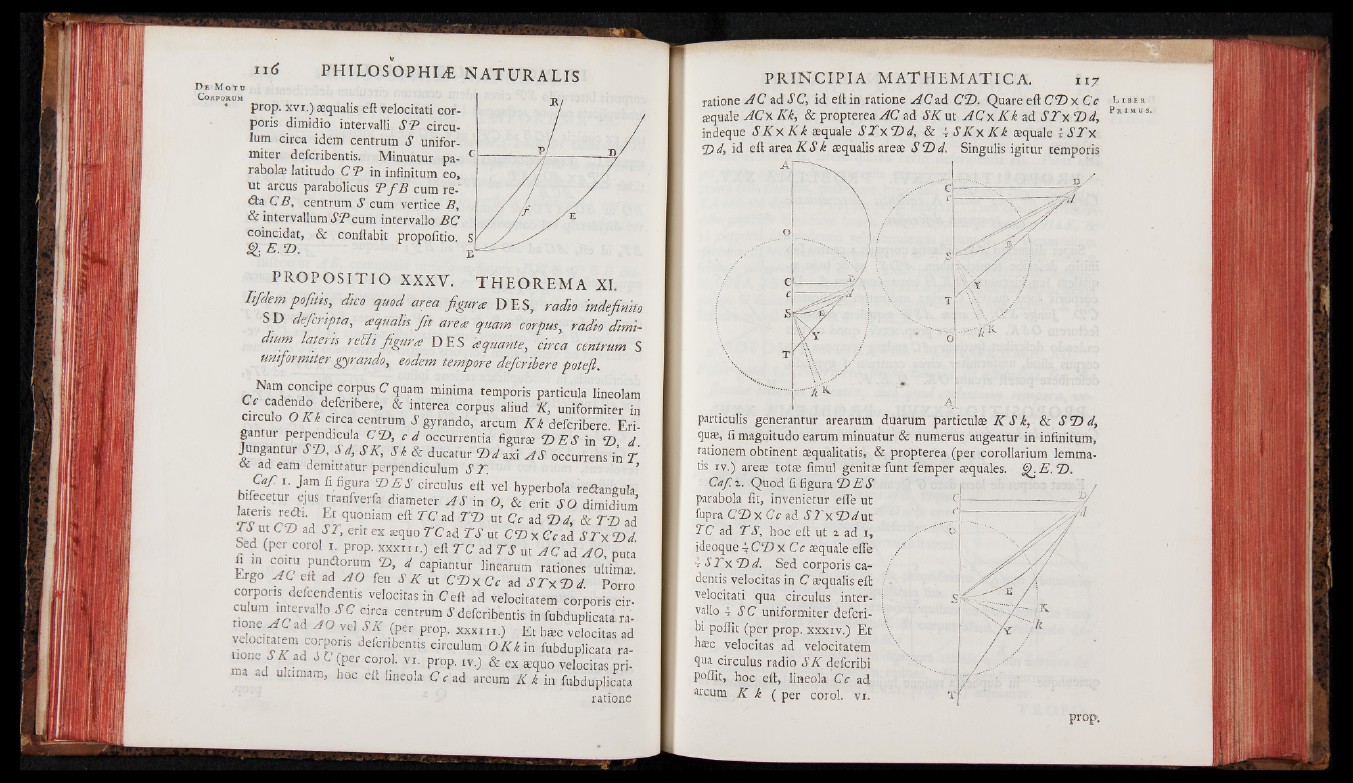
Nam concipe corpus C quam minima temporis particula Iineolam
K ì B H M & lnterea corPus aliud "K, uniformiter in
circulo O K k circa centrum J gyrando, arcum K k defcribere. Eri-
gantur perpendicula C D , c d occurrentia figura D E S in D d
Jungantur SD , Sd, SK, Sk & ducatur D d axi A S occurrens in T
oc ad earn demittatur perpendiculum ST. ’
C af i . Jam fi figura D E S circulus eft vel hyperbola reéfangula
bifecetur ejus tranfverfa diameter A S in O, & erit SO dimidium
? r qUOniam TS ut C D ad ST, erit ex teeqfut or ICTaC dad TTTS> u«t C D x Gc ad S TBx D d ad.
bed (per corol i prop, xxxn i.) eft T C ad T S ut A C ad AO, puta
EErrgÌoo CTA Cc Pef7t aRfd 0rAJ O71 1freDu ,Jf K^ aupt iZCmDmx CIince aardu mS TraxtiDonde.s ulPtiomrrao:.
corporis defcendentis veloeitas in Ceft ad velocitatem corporis cir-
rione” Ì S circa centrum d'defcribentis in fubduplicata ra- 1? . Vel SK Cper prop, xxxm.) Et trac veloeitas ad
r i o n e ' I B P circulum O / a in fubduplicata rama
ad ir- H I U S I VI' pr0p' I V * ex SE^U0 vel°citas pri-
ultimam, hoc eft hneola Cc ad arcum K k in fubduplicata
ratione
ratione A C ad SC, id eft in ratione A Cad CD. Quare eft C D x Cc Libek
aequale ACx Kk, & propterea AC ad SK ut A C x Kk ad S T x Dd, p * 1M u s-
indeque SKX Kk aequale S T x D d , & ì S K x K k aequale i S T x
Dd, id eft area K S k aequalis areae SDd. Singulis igitur temporis
particulis generantur arearum duarum particulae K S k , & S D d ,
quae, fi magnitudo earum minuatur & numerus augeatur in infinitum,
rarionem obtinent aequalitatis, & propterea (per corollarium lemma-
tis iv.) areae totae fimul genitae funt femper aequales. Q. E . D.
Caf. z. Quod fi figura D E S
parabola fit, invenietur effe ut
fupra C D x Cc ad S l 'xDdwt
TC ad TS, hoc eft ut z ad 1,
ideoque i CD x Cc aequale effe
4 S T xD d . Sed corporis ca-
dentis veloeitas in C aequalis eft
velocitati qua circulus intervallo
1- SC uniformiter deferi-
bi poflit (per prop.,xxxiv.) Et
haec veloeitas ad velocitatem
qua circulus radio SK cìefcribi
polfit, hoc eft, lineola Cc ad
atcum K k ( per corol. vi.
prop.