hoogte dan 4800 Ned. ellen hebben», gaan dus slechts een weinig den
Mont Blanc te boven, die 4813 Ned. ellen hoog is. Vergelijkt men
echter deze hoogten met de ligchamen, waarop zij zich bevinden, dan
zijn die op de maan veel aanzienlijker te achten. Want terwijl de
hoogste hoogte der bergen op de aarde slechts het 1481s,e gedeelte van
hare middellijn bedraagt, is die op de maan het 4548te gedeelte.
Welligt verwondert zich iemand daarover, dat de sterrekundigen
ons niet alleen het bestaan der bergen op de maan verzekeren, maar
ook zelfs hunne hoogte aangeven. De wijze, waarop dit plaats heeft,
is echter zoo moeijelijk niet te verklaren. Men ontdekt dikwijls in
de nabijheid van de scheidlijn tusschen de dag- en nachtzijde der
maan op het donkere gedeelte enkele lichte punten, die gedurig
grooter worden en meer naar de dagzijde naderen, totdat zij eindelijk
geheel in het licht zijn gekomen. Dit verschijnsel laat zich zeer gemakkelijk
verklaren. De zonnestralen worden in hun Joop eerst opgevangen
en teruggekaatst door bergtoppen, wier voet nog niet door de
zon beschenen wordt, die zich dus nog aan de nachtzijde bevindt.
Als men nu den afstand tusschen deze lichtpunten en de lichtzijde of
de dag- en nachtgrens der maan naauwkeurig meet, dan valt hét
gemakkelijk daaruit de hoogte van zulk een bergtop te berekenen.
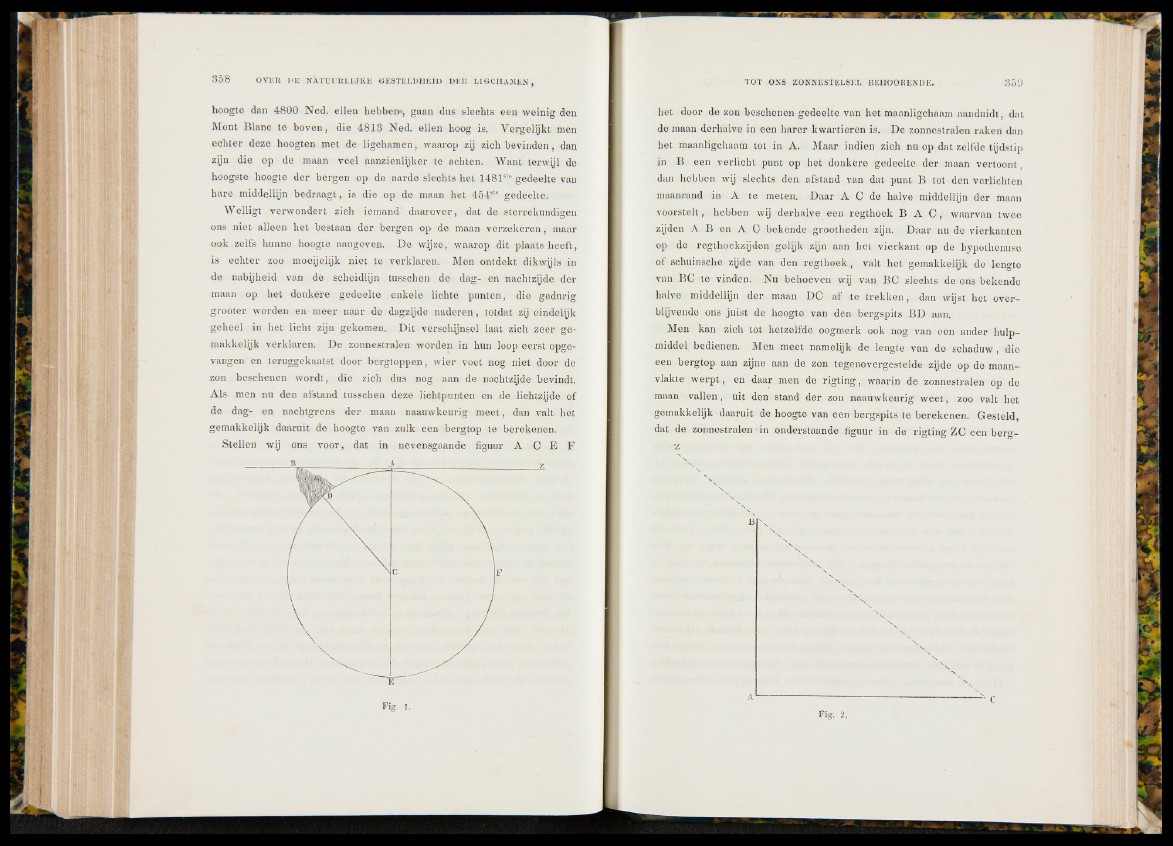
Stellen wij ons voor, dat in nevensgaande figuur A C E E
Kg. 1.
359
het door de zon beschenen gedeelte van het maanligchaam aanduidt, dat
de maan derhalve in een harer kwartieren is. De zonnestralen raken dan
het maanligchaam tot in A. Maar indien zich nu op dat zelfde tijdstip
in B een verlicht punt op het donkere gedeelte der maan vertoont,
dan hebben wij slechts den afstand van dat punt B tot den verlichten
maanrand in A te meten. Daar A C de halve middellijn der maan
voorstelt, hebben wij derhalve een regthoek B A C , waarvan twee
zijden A B en A C bekende grootheden zijn. Daar nu de vierkanten
op de regthoekzijden gelijk zijn aan het vierkant op de hypothenuse
of schuinsche zijde van den regthoek , valt het gemakkelijk de lengte
van BC te vinden. Nu behoeven wij van BC slechts de ons bekende
halve middellijn der maan DC af te trekken, dan wijst het overblijvende
ons juist de hoogte van den bergspits BD aan.
Men kan zich tot hetzelfde oogmerk ook nog van een ander hulpmiddel
bedienen. Men meet namelijk de lengte van de schaduw, die
een bergtop aan zijne aan de zon tegenovergestelde zijde op de maan-
vlakte werpt, en daar men de rigting, waarin de zonnestralen op de
maan vallen , uit den stand der zon naauwkeurig w eet, zoo valt het
gemakkelijk daaruit de hoogte van een bergspits te berekenen. Gesteld,
dat de zonnestralen in onderstaande figuur in de rigting ZC een berg-
H
---------c