DUIN D IC A T IO N I BAROM È TR E . |
HAUTEURS CORRESPONDANTES J DC BAR.
N* I. MIL L IM È T \ oM È T R E .
9- 8. 7. | 6. 5. 8. 1
c e n t . m è t r e s . m è t r e s . m è t r e s . m è t r e s . 0,0 10,2 3o,8 r a PPf è t r e s m è t r e s . m è t r e s .
77 20,5 832 9)3
76 io 3,o I i 3,4 123,8 i34,2 x44»6 8,3 9)4
75 207,5 2x8,0 228,5 23g ,i 249,^ 8,5 9)5
74 3 i 3,3 324,0 334,7 345,4 356, i 8,6 9.8
73 420,4 43 X, X 44x,8 452,6 463,5 8,7 9,8
7 3 529,2 540,2 55x, x 562,0 573,0 8,8 9-9
7 * 639,4 65o,6 661,7 672,8 683,9 75i 8,9 10,0
70 ,X 762,4 773,7 785,0 796,3; 9,0 10,2
69 864,4 875,8 887,3 898,7 9x0,2 9)2 10,4
68 979)4 9 9U° 1002,6 io i4,3 1025.9 9 .3 10,5
67 1096,0 x 107,8 1119,5 x i 3x,3 xx43, 1 9)4 xo,6
66 1214,4 1226,3 1238,2 i 25o,3 1262,3 9 >6 10,8
65 i334,7 i 346,8 i358,9 x37 1,0 x383,2 64 1 4 5 6 , 7 1469,0 i48i ,3 i493,6 9)8 11,0
i 5o6,o 9)9 XI,2
63 i 58o,5 i593,o i6o5,5 x6x8,o i 63o,6 IO, I i i ,3
6 2 1706,4 T7 l 9>z 1732,8 1744,6 1757,4 10,2 xi, 5
61 i 834,3 ï847,i 1860,0 1872,9 1885,9 2ûo3,6 10,4 l l ->7
60 1964,3 1977»4 1990,5 2016,7 10,6 iU 9
59 2096,4 2x09,7 2123,0 2 x36,4 2149,8 223o,8 10,7 12,1
58 2244,3 2257,9 2271*5 2285,1 238i ,2 I0 )9 12,2
*7 2367,4 2395,0 2408,9 2422,8 56 25o6,5 11,1 12,5
2520,5 2534,5 2548,6 2562,7 n ,3 12,7
55 2648,0 2662,3 2676,6 2691,0 2705,3 n,5 x3 ,o
2792,0 2806,7 2821,3 2835,9 285o,6XI,8 x 3,2
1 54
1 53 2939,0 2953,8 2968,6 2983,5 2998,4 12,0 1 i 3,5
Résultat plus grand de 6 mètres que celui donné par la
mesure trigonométrique. Cette différence, sur une si grande
hauteur, doit être regardée comme nulle; outre qu’elle rentre
J presque dans la limite des erreurs de l’observation , des con- I s idérations ultérieures nous feront voir que, vu l’heure des
observations au Mont-Grégorio, leur résultat devait pécher
un peu en excès. Nous pouvons donc conclure , de notre
comparaison entre les deux modes de mesurer les hauteurs,
que la formule que nous avons établie donne des résultats
rtussi exacts qu’on peut l’espérer de la méthode barométrique.
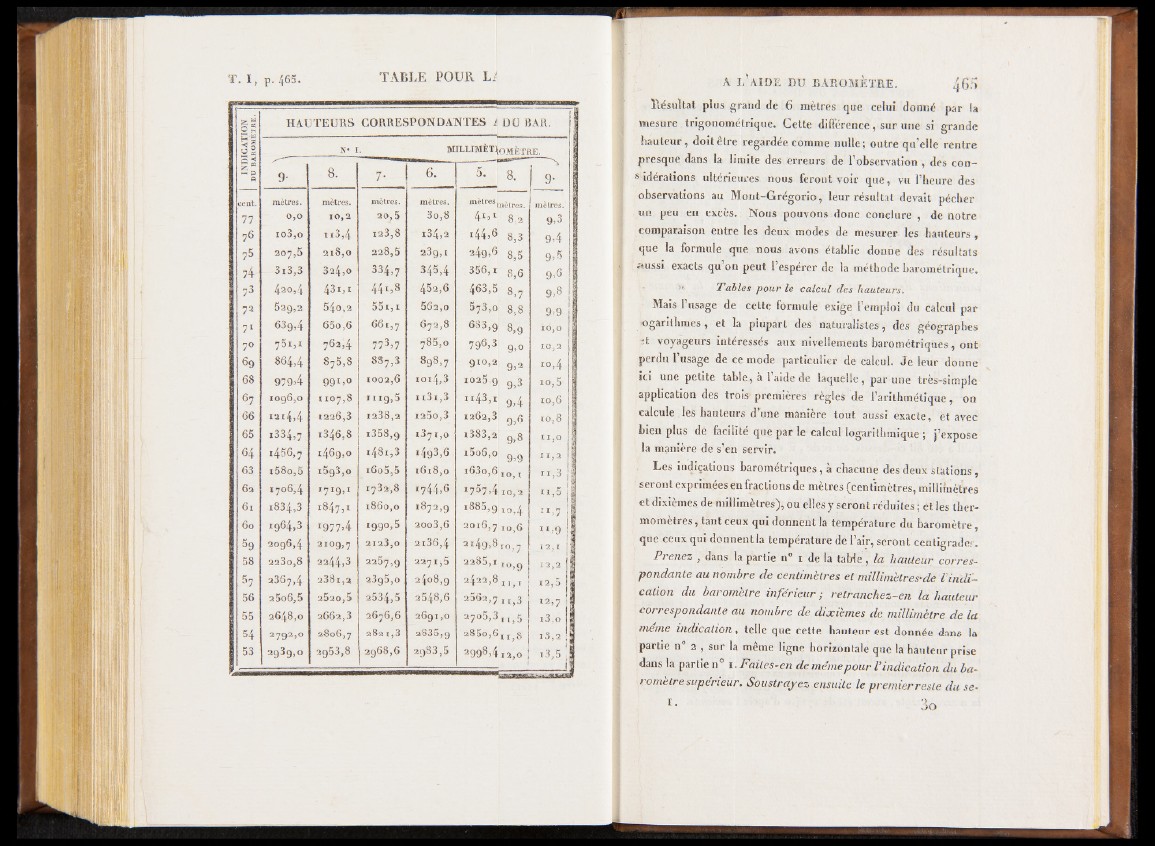
Tables pour le calcul des hauteurs.
Mais l’usage de cette formule exige l’emploi du calcul par
ogaiithmes, et la plupart des naturalistes, des géographes
it voyageurs intéressés aux nivellements barométriques , ont
perdu l’usage de ce mode particulier de calcul. Je leur donne
ici une petite table, a 1 aide de laquelle, par une très-simple
application des trois- premières règles de l’arithmétique, on
calcule les hauteurs d’une manière tout aussi exacte, et avec
bien plus de facilité que par le calcul logarithmique ; j’expose
la manière de s’en servir.
Les indications barométriques, à chacune des deux stations,
seront exprimées en fractions de mètres (centimètres, millimètres
et dixièmes de millimètres), ou elles y seront réduites ; et les thermomètres,
tant ceux qui donnent la température du baromètre
que ceux qui donnent la température de l’air, seront centigrades.
Prenez } dans la partie n° i de la table, la hauteur correspondante
au nombre de centimètres et millimètres'de l'indication
du baromètre inférieur ; retranchez-en la hauteur
correspondante au nombre de dixièmes de millimètre de la
meme indication, telle que cette hauteur est donnée dans la
partie n° 2 , sur la même ligne horizontale que la hauteur prise
dans la partie n° 1. Faites-en de meme pour V indication du baromètre
supérieur. Soustrayez ensuite le premier reste du se