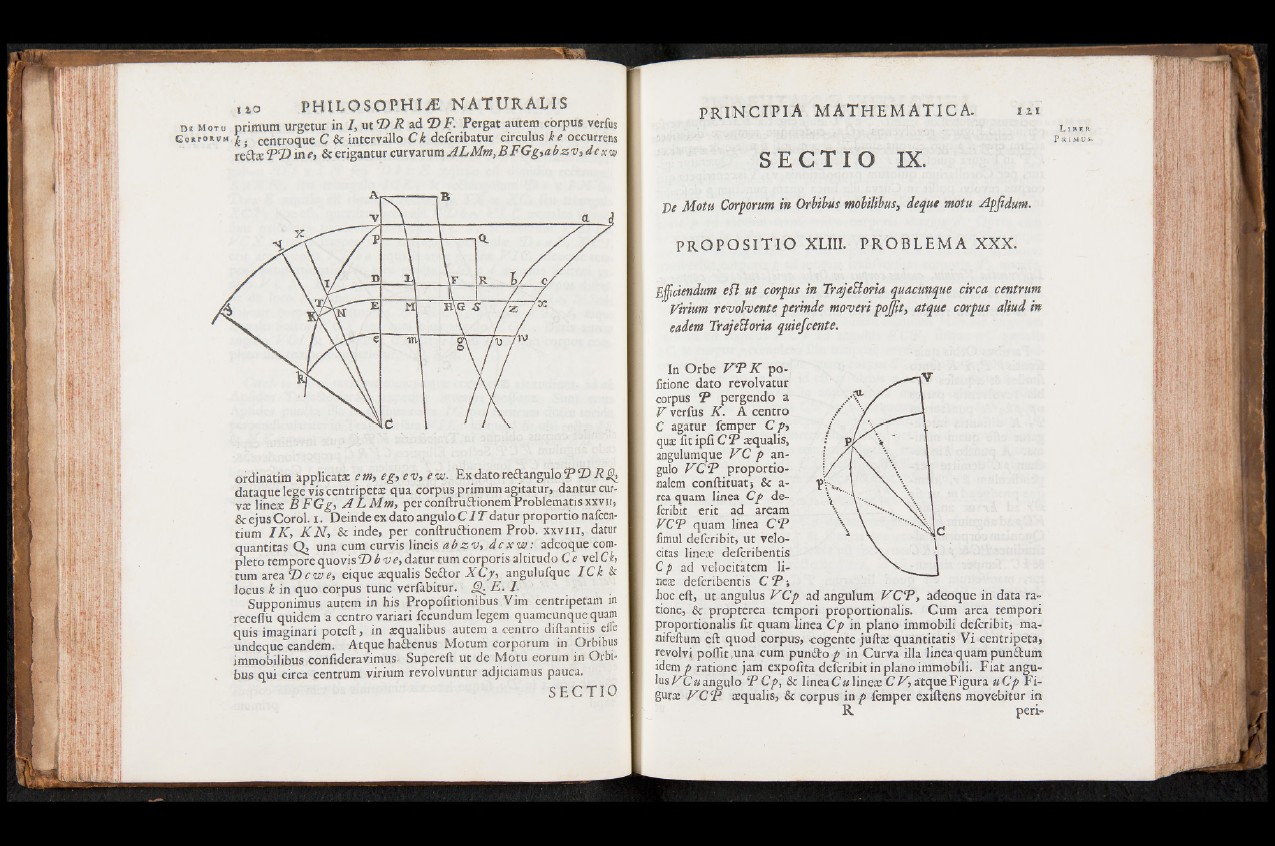
IZO PHILOSOPHIC NATURAL I S
D t M o t u primum urgetur in I, ut © F ad © F . Pergat autem corpus verfus
GonronuM^. centroque C Sc intervallo Ck defcribatur circulus ke oecurrens
re it« F© in e, Sceriganturcurvarum ALMm,BFGg,abzv,dcxw
ordinatim applicata: em, eg,, ev, e w. Ex dato reftangulo T D R ^
d a t a q u e lege vis centripeta qua corpus primum agitatur, danturcur-
V« line« B F G g , A LM m , perconftructionemProblematisxxvir,
& ejus Corol. i. Deinde ex dato angulo C I T datur proportio nafcen-
tium IK , K N , Sc inde, per conftru&ionem Prob. xxvm,. datur
quantitas Q, una cum curvis lineis a b z v , dcxw: adeoque completo
tempore quovis D b ve, datur turn corporis al titudo C e vel C k,
turn area © c w e, eique «qualis Seitor XCy, angulufque IC k &
locus k in quo corpus tunc verfabitur. E. I.
Supponimus autem in his Propofitionibus Vim centripetam in
receflu quidem a centro variari fecundum legem quamcunque quam
quis imaginari poteft, in «qualibus autem a centro diftantiis effe
undeque eandem. Atque ha&enus Motum corporum in Orbibus
immobilibus confideravimus. Supereft ut de Motu eorum in Orbibus
qui circa centrum virium revolvuntur adjiciamus pauca.
SECTIO
PRINCIP I A MATHE MAT ICA . im
, Liber
Primus» SECTIO IX.
De Motu Corporum in Orhibus mobilihus, deque motu Apfidum.
PROPOSITIO XLIII. PROBLEMA XXX.
pjjiciendum eil ut corpus in Traj(Boria qualunque circa centrum
Virium revoléente perinde moveri pojfit, atque corpus aliud in
eadem TrajeBoria quiefcente.
In Orbe V T K po-
fitione dato revolvatur
corpus T pergendo a
V verfus K. A centro
C agatur femper C p ,
qu« fit ipfi C T «qualis,
angulumque V C p angulo
V C T proportionalem
conftituat} Sc a-
rea quam linea Cp de-
fcribit erit ad aream
VCT quam linea C T
ilmul defcribit, ut velo-
citas line« defcribentis
Cp ad velocitatem line
« defcribentis CT-,
hoc eli, ut angulus VCp ad angulum V C T , adeoque in data ra-
tione, Sc propterea tempori proportionalis. Cum area tempori
proportionalis fit quam linea Cp in plano immobili deicribit, ma-
niftftum eft quod corpus, cogente juft« quantitatis Vi centripeta,
revolví poifit >una cum punito/» in Curva illa linea-quam punctum
idem/» ratione jam expofita defcribit in plano immobili. Fiat angu-
lus V C« angulo TCp, Se linea C u line« C V, atque Figura uCp Figur
« VC T «qualis, & corpus in p lèmper exiftens movebitur in
R peri