• D i M o t u
' C o r p o r u m P R O P O S I T I O X C V I . T H E O R E M A L.
lifdem pofitis & quod, motus ante incidentiam melocior f i t quam
pofiea: die o quod corpus, inclinando line am incidentite, reße.
iletur tandem, & angulus reflexionis fiet aqualis ángulo incu
dent'ue.
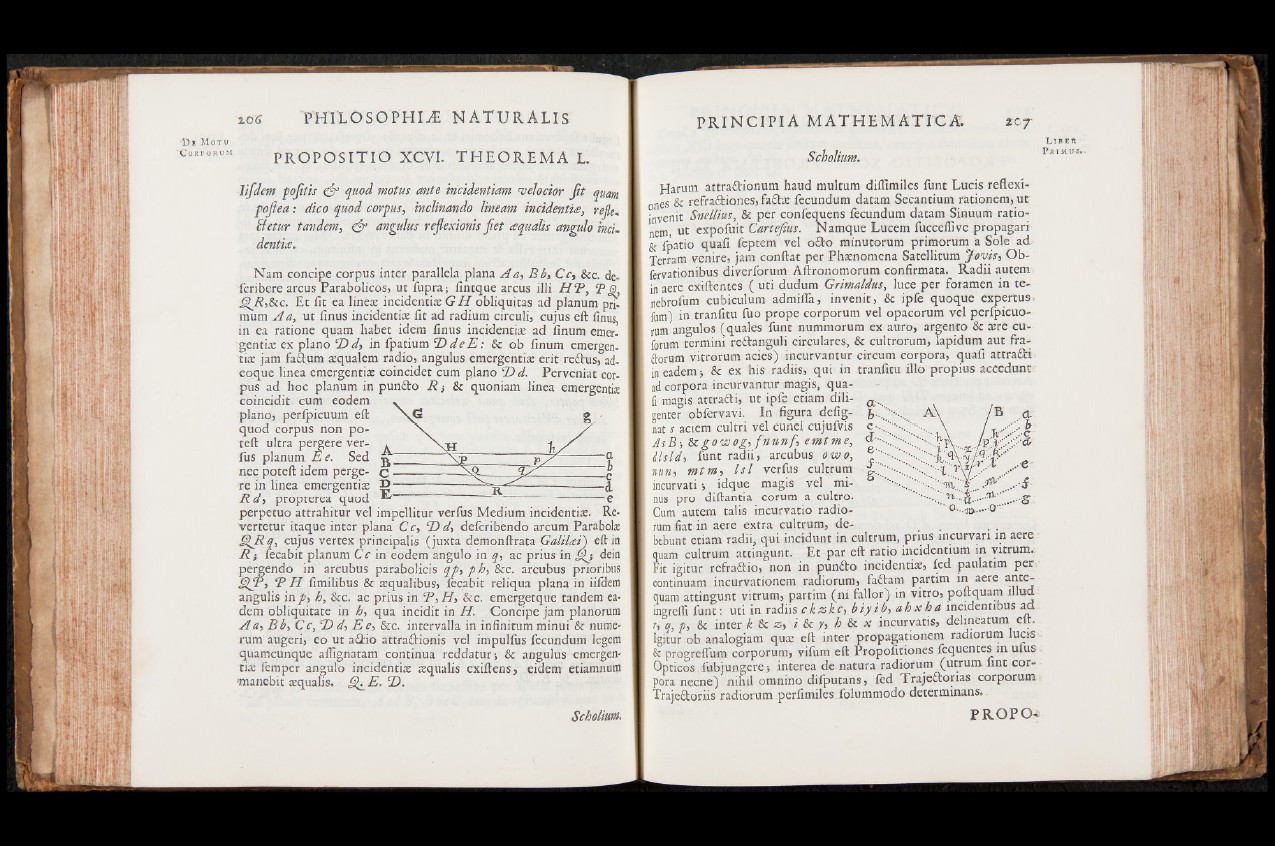
Nam concipe corpus inter parallela plana Aa ,B b , Cc, &c. de-
feribere arcus Parabolicos> ut fupra; fintque arcus illi HR , BQ,
£)jR,ikc. Et fit ea lines incidentis G H obliquitas ad planum pfi.
mum A a, ut finus incident is fit ad radium circuli, cujus eft finus,
in ea ratione quam habet idem finus incidentis ad finum emergentis
ex plano D d , in fpatium D d e E : & ob finum emergen-
tis jam fa£lum squalem radio, angulus emergentis erit redtus, ad-
eoque linea emergentis coincidet cum piano dJ d. Perveniat corpus
ad hoc planum, in pundto R ¡ & quoniam linea emergentis
coincidir cum eodem
piano, peripicuum eft
quod corpus non po-
reft ultra pergere ver-
iiis planum Ee. Sed
nec poteft idem perge- i
re in linea emergentis 1
R
Rd , propterea quod
perpetuo attrahitur vel impellitur verfus Medium incidentis. Re-
vertetur itaque inter plana Cc, E>d, defcribendo arcum Parabola*
Q R q , cujus vertex principalis (juxta demonftrata Galilai) eft in
R } fecabit planum CV in eodem angulo in q, ac prius in dein
pergendo in arcubus parabolicis qp, p h , &c. arcubus prioribus
QpP, *P H fimilibus & squalibus, fecabit reliqua plana in iifdem
angulis inp, h, &c. ac prius in R, H, &c. emergetque tandem ea-
dem obliquitate in h, qua incidit in H. Concipe jam planorum
A a, Bb, C c,dD d, E e, Ike. intervalla in infinitum minui 8c nume-
rum augeri, eo ut adio attra&ionis vel impulfus fecundum legem
quamcunque ailignatam continua reddatur; & angulus emergentis
femper angulo incidentis squalis exiftens, eidem etiamnum
smanebit squalis. £^E. D .
Scholium•
Scholium.
Harum attradbionum haud multum diillmiles funt Lucis reflexi-
ones & refradtiones, fadts fecundum datam Secantium rationem,ut
invenit Snellius, & per confequens fecundum datam Sinuum ratio-
nem, ut expofuit Cartefius. Namque Lucem fucceflìve propagar!
gc fpatio quafi feptem vel odio minutorum primorum a Sole ad
Terram venire, jam conftat per Phsnomena Satellitum Jovìs, Ob-
fervationibus diverforum Aftronomorum confirmata. Radii autem
in aere exiftentes ( uti dudum Grimaldus, luce per foramen in te-
nebrofum cubiculum admifià, invenit, & ipfe quoque expertus-
fum) in tranfitu fuo prope corporum vel opacorum vel perfpicuo-
rum angulos (quales funt nummorum ex auro, argento & sre cu-
forum termini redtanguli circulares, & cultrorum, lapidum aut fra--
ftorum vitrorum aeies) incurvantur circum corpora, quafi attradìi
ineadem; & ex his radiis, qui in tranfitu ilio propius acCedunt:
ad corpora incurvantur magis, quafi
magis attradìi, ut ipfe edam dili-
s—
genter obfervavi. In figura defig-
li A\ /B m m A -
nat s aciem cultri vel cunei cujufvis
c-.. H
.c AsB-, 8cgowog, fnunf , emtme,
e-.„ "■
S a g ffil H i - d> ilsld, funt radii, arcubus owo,
nun, mtm, Isl verfus cultrum
S19< " 1 \••••\ H W il/ ..e- incurvati ; idque magis vel mi-
C* . . . .
nus prò diftantia eorum a cultro.
................1 . . . . ■ S
Cum autem talis incurvarlo radio-
' O' rum fiat in aere extra cultrum, de- _ .
bebunt etiam radii, qui incidunt in cultrum, prius incurvari in aere
quam cultrum attingunt. Et par eft ratio incidentium in vitrum.
Fit igitur refrailioj non in punito incidenti^ fed paulatim per:
continuam incurvationem radiorum, fadlam partim in aere ante-
quam attingunt vitrum, partim (ni fallor) in vitro, poftquam illud
ingrefli funt: uti in radiis ckzkc , biyib, a h xha incidentibus ad
r, q, p, 8c inter k 8c z> i 8c y, h & x incurvatis, delineatum eft.
Igitur ob analogiam qus eft inter propagationem radiorum luets
& progreifum corporum, vifum eft Propofitiones fequentes m ulus
Opticos fubjungere; interea de natura radiorum (utrum fint corpora
necne) nihil omnino difputans, fed Trajedtorias corporum
Trajedoriis radiorum perfimiles folummodo determinans.
P R O P O»
Líber
P r i m u=Sé