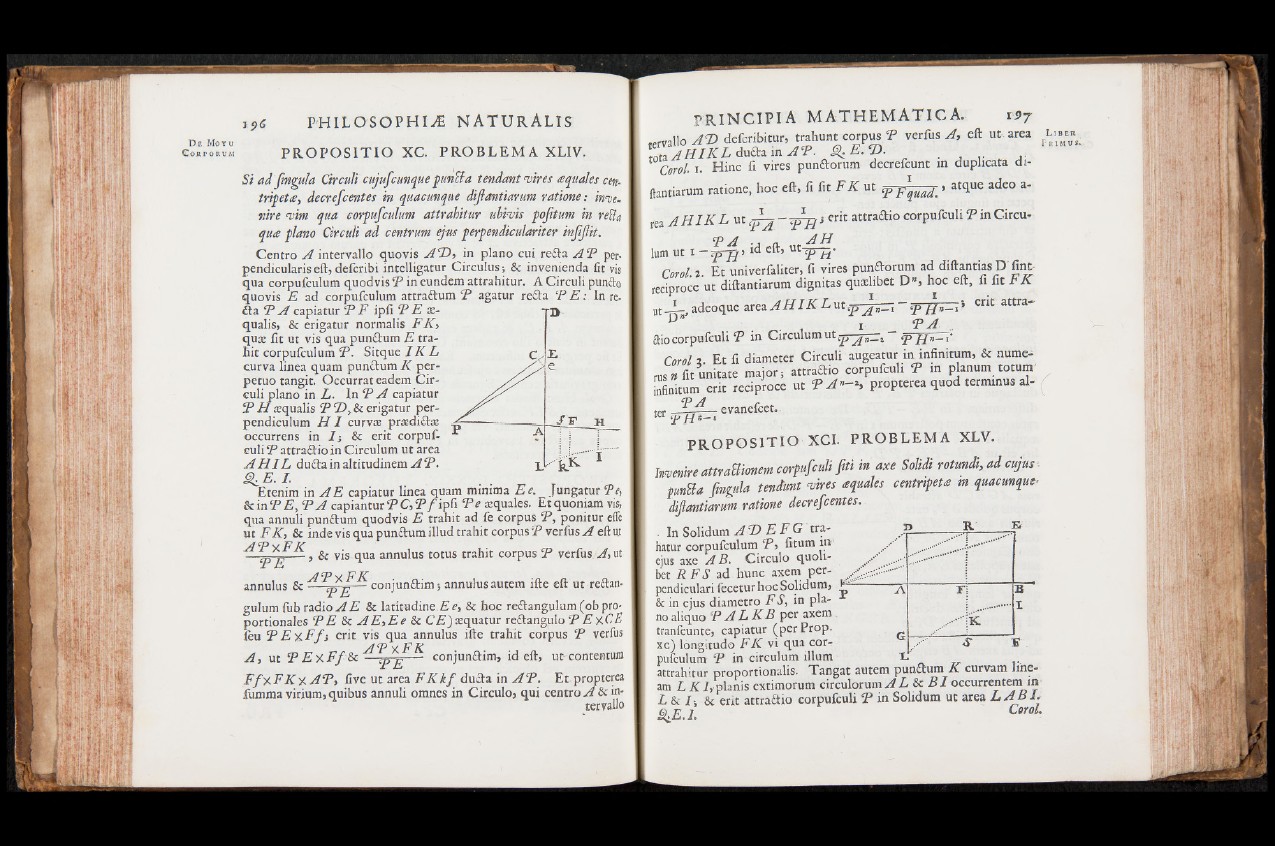
P R O P O S I T I O XC. P R O B L E M A XLIV.
Si ad faglila Circuii cujufcunque puntila tendoni mires aquales ct%
tripete, decrefcentes in quacunque difantiarum ratione: invertire
mim qua eorpufculum attrahitur ubimis pofaum in reUct
qu<e plano Circuii ad centrum ejus perpendiculariter infifat.
Centro A intervallo quovis AT>, in plano cui reità A P per-
pendiculariseft, defcribi intelligatur Circulus; & invenienda fìt vis
qua eorpufculum quodvisT3 ineundem attrahitur. A Circuii punita
quovis E ad eorpufculum attra&um P agatur reità ‘P E : Ln re.,
¿la P A capiatur P F iplì P E x-
qualis, & erigatur normalis F K ,
qua: fit ut vis qua punitum E trahit
eorpufculum P . Sitque I K L
curva linea quam punitum K perpetuo
tangit. Occurrat eadem Circuii
plano in L. ln P A capiatur
P H asqualis PT>y&i erigatur per-
pendiculum H I curvìe praediita:
occurrens in 7j & erit corpufculi
T3 attraitio in Circulum ut area
A H I L duita in altitudinem P .
Q .E . I.
Etenim in A E capiatur linea quam minima E e. Jungatur 9 e,
& in P E, P A capiantur P C, P f ìpfi 9 e asquales. Et quoniam vis,
qua annuii punitum quodvis E trahit ad le corpus P , ponitur effe
ut F K , & inde vis qua punitum illud trahit corpus P verfus A eftut
A CD ks W
, & vis qua annulus totus trahit corpus P verfus A, ut
Jr he
a cp sj Ti jr
annulus & epE— conjun^ rn > aimulusaiitem ifte eft ut reitangulum
fub radio A E Se latitudine. E e, & hoc reitangulum (ob pròportionales
P E & A E-, E e & CE ) aequatur reitangulo PEy.CE
leu P E % F f i erit vis qua annulus ifte trahit corpus P verfus
A P -n F K . . . . „
A i ut P E yFf&c — p ~£ ~— conjunitim, id eft, ut contermini
F fy .FK y .A P t live ut area F K k f duita in A P . Et propterea
fumma virium, quibus annuii omnes in Circulo, qui centro A & intervallo
1 AT) defcribitur, trahunt corpus P verfus Ay eft ut area
— — B R i I Corol. i Hinc ft vires punitorum decrefcunt m duplicata di-
ftantiarura ratione, hoc eft, ft fit F K ut » atque adeo atea
A H I K L ut e]~ - Tpjqi erit attraitio corpufculi P in Circu-
P A H i ,,t A H
lum ut i p t i '
Corol. i- Et univerfaliter, fi vires punitorum ad diftantias D fint-
reciproce ut diftantiarum dignitas quaelibet D ”, hoc eft, fi fit F K
ut —, adeoque area A H I K L ut p~A^zi '
D P H ■-**
P A
erit attra-
• ^, - 1 1 — P A -
Ûio corpufculi T in Circulum ut¿p ^ * P H n~~ i*
Corol z. Et fi diameter Circuli augeatur in infinitum, & nurne-
rus » fit unitate major; attraftio corpufcuh P in planum totum
infinitum erit reciproce ut P A — y propterea quod terminus al- £
tpr _ ‘P ^ _ evanefcct.
9 H*~l
P R O P O S I T I O XCI. P R O B L E M A XLV.
hvenire attraBionem corpufculi fat in axe Solidi rotundi, ad cujus ■
puntta fagula tendunt mires aquales centripète m quacunquc
difantiarum ratione decrefcentes.
. In Solidum H E F G tra- M 13 -----H R ----- H
E
h a t u r c o r p u f c u l u m “P , f i t u m l » ' ..••• ■ )
ejus axe A B. Circulo quoli- ,
bet R F S ad hunc a x e m perp
A ■ B
x1
e n d i c u l a r i f e c e t u r h o c S o l i d u m , . y j & in ejus diametro FS, in pla- ; _ ^
I
no aliquo P A L K B per axem : ,.<";¡k
k
tranfeunte, capiatur (per Prop. ;_____
xc) longitudo F K vi qua cor- \s
4* If
pufculum P in circulum ilium X.
attrahitur proportionalis. Tangat autem punitum K curvam Iine-
am L Kly planis extimorum circulorum A L & B I occurrentetn in
L&c I ; & erit attraitio corpufculi P in Solidum ut area L A B I .
$ .E .l. CeroL
L i b e *
Primus.,