D e Mo t u
CoRforum P R O P O S I T I O II. T H E O R E M A II.
Si Corsovi reßßitur in ratione velocitatis, & idem fola vi ìnfitg
per Medium fimilare moveatur,fumantur autem tempora aqua*
Ha : velocitates in principììs fngulorum temporum funt in pro-
greßone Geometrica, & ßatia fingulis temporibus defcripta
funt ut velocitai es.
Cas. i. Dividatur tempus in partículas aequales; & fi ipfis parti,
cularum initiis agat vis refiftentiae impulfo unico, quce fit ut velo-
citas: erit decreraentum velocitatis fingulis temporìs particulis ut
cadem velocitas. Sunt ergo velocitates differentiis fifis proportio-
nales, Se propterea (per Lem. i. Lib. n.) continue proportionales.
Proinde fi ex acquali particularum numero compo/tantur tempora
quaelibet squalia, erunt velocitates ipfis temporum initiis, ut termini
in progreffione continua, qui per faltum capiuntur, omilfo
paflìm acquali terminorum intermediorum numero. Componuntur
autem horum terminorum rationes ex aequalibus rationibus terminorum
intermediorum tequaliter repetitis, Se propterea funt ¡equates.
Igitur velocitates, his termini's proportionales, funt in pro-
greffione Geometrica. Minuantur jam aequales illa: temporum par-
ticulae, Sc augeatur earum numerus in infinitum, eo ut refiftentia:
impulfus reddatur continuus-, & velocitates in principiis aequalium
temporum, femper continue proportionales, erunt in hoc etiam
cafu continue proportionales. G^E.D.
Cas. 2. Et divifim velocitatum differentiae, hoc eft, earum partes
fingulis temporibus amiffae, funt ut tota;: Spatia autem fingulis
temporibus defcripta funt ut velocitatum partes-amiflàe, (per Prop.
ì.Lib. il.) Se propterea etiam ut totee. E. CD.
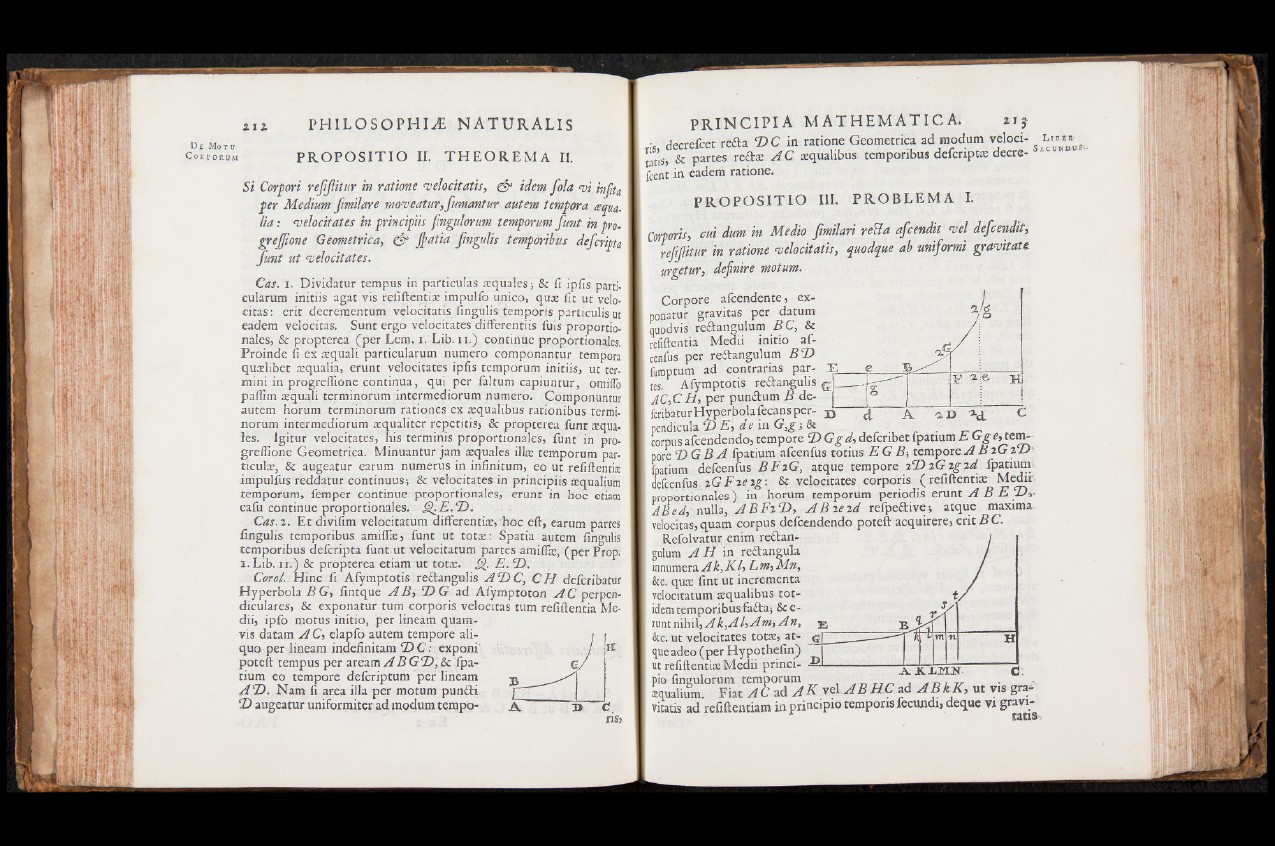
Corol. Hinc fi Afymptotis rettangulis A D C , C H deferibatur
Hyperbola B G, fintque A B , D G ad Afymptoton A C perpendiculares,
& exponatur turn corporis velocitas tum refiftentia Me-
dii, ipfo motus initio, per Mneam quam-
vis datam A C, elapfo autem tempore ali-
quo per lineam indefinitam D C : exponi
poteft tempus per aream A B G D , & fpa-
tium eo tempore deicriptum per lineam
A D . Nana fi area illa per motum puniti
SD augeatur uniformiter ad modum tempo-
PRINCIP IA MATHEMATICA- »
• jeerefeet reita D C in ratione Geometrica ad modum veloci-
tatk Se partes retta: A C aequalibus temporibus defcripta: decre-
feent in eadem ratione.
P R O P O S I T I O III. P R O B L E M A I.
Corporis, cui dum in Medio fimilari retta afeendit vel defeendit,
refifiitur in ratione 'velocitatis, quodque ab uniformi gravitate:
definire motum.
Corpore afeendente, exponatur
gravitas per datum
quodvis rettangulum BC, Se
refiftentia Medii initio af-
cenfus per rettangulum B D
fumptum ad contrarias par-
! tes.' Afymptotis rettangulis
I AC,C Hi per punttum B de4n
t
E e
r ß / I
■ii
1
e h
•f a n __ 1-----
ci A iD
pendicula D E, de in G,gs Se r
corpus afeendendo, tempore D Ggd, defenbet fpatium E Gg e, tannar
e D G B A fpatium afeenfus totius E G B-, tempore A B iG 2 x>
fpatium defeenfus B F iG , atque tempore zDzGzgzd fpatium
defeenfus iGFze ig: Se velocitates corporis (refiftentia Medir
proportionales ) in horum temporum periodis erunt A B E D , .
AB ed, nulla, A B F iD , A B z e z d refpeftive-, atque maxima
velocitas, quam corpus defeendendo poteft acquirere, erit B C.
Refolvatur enim rettangulum
A H in rettangula
innumera Ak,Kl ,Lm,Mn,
&c. qua: fint ut incrementa
velocitatum aequalibus tot-
idem temporibus fatta; Se erunt
nihil, A k,Al, Am, A n ,
&c. ut velocitates totae, atque
adeo (per Hy pothefin)
ut refiftentia: Medii princi- -----------------
^ F T a K ^ A B H C ? A B k K , « vù gravitatis
ad refiftentiam in principio temporìs fecundi, deque vi gravi tatis
Liber*
ECUND-U^«-