t s PHILO SOPHI E N A T U R A L I S
centium arcuum ab, bc, ed, &c. comprehenditur, coincidit ultimo
cum Figura curvilinea.
Corol. 3. Ut & Figura rettilinea circumfcripta qua: tangentibus
eorundem arcuum comprehenditur.
Corol. 4. Et propterea ha: Figura: ultima: (quoad perimetros acE,')
non funt rettilinea:, fed rettilinearum limites curvilinei.
L E M M A IV.
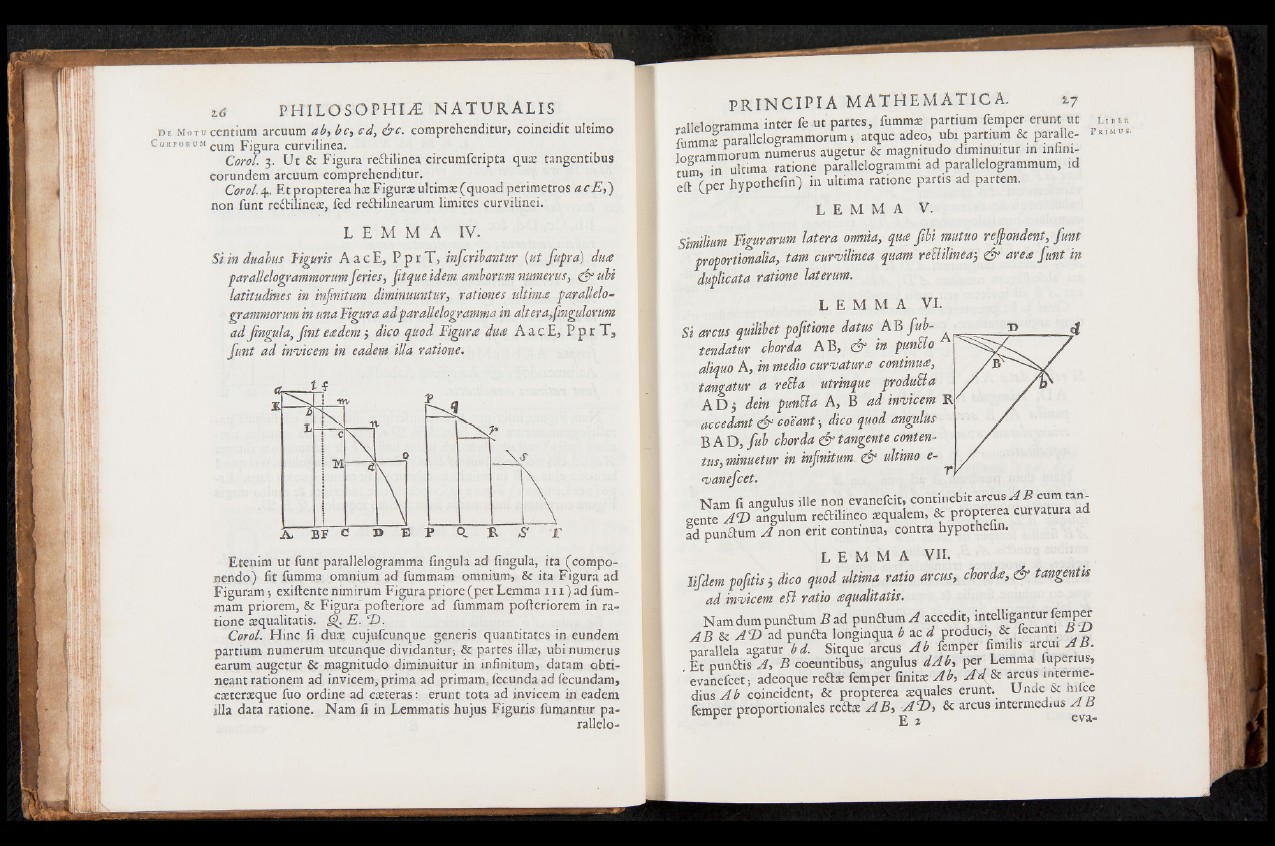
Si in duabus Tiguris A ac E, P p r T, infcribantur [ut fupra) dua
paraUelogrammorum feries, fitque idem amborum numerus, & ubi
latitudines in injinitum diminuuntur, rationes ultima parallelo-
grammorum in una Figura ad parallelogramma in altera,fingulorum
ad Jìngula, jin t eadem j dico quod Figura dua A a c E, P p r T,
funt ad invicem in eadem iUa ratione.
■ H
■ H8
\
E BF C » E P CL R S 1
Etenim ut funt parallelogramma lingula ad lìngula, ita (componendo)
fit fumma omnium ad fummam omnium, & ita Figura ad
Figuram ; exilíente nimirum Figura priore (per Lemma 111) ad fummam
priorem, & Figura pofleriore ad fummam pofleriorem in ratione
xqualitatis. Q. E. E>.
Corol. Hinc fi dua cujufcunque generis quantitates in eundem
partium numerum utcunque dividantur; & partes illa, ubi numerus
earum augetur & magnitudo diminuitur in infinitum, datam obti-
neant rationem ad invicem, prima ad primam, fecunda ad fecundara,
cateraque fuo ordine ad caceras : erunt tota ad invicem in eadem
illa data ratione. Nam fi in Lemmatis hujus Figuris fumantur parallelom
P R I N C I P I A M A T H E M A T I C A . 1 7
rdlelogramma inter fe ut partes, fumma: partium femper erunt ut
fi,mma paraUelogrammorum > atque adeo, ubi partium & paralle-
” rammorutn numerus augetur & magnitudo dimmuitur in .infinitum
in ultima ratione parallelogrammi ad parallelogrammum, id
eft (per hypothefin) in ultima ratione partis ad partem.
L E M M A V.
Simìlium Figurarmi latera omnia, qua fibi mutuo refiondent, funt
proportionalia, tam curvilinea quam rettilinea^ & area funt
duplicata ratione laterum.
L E M M A VI.
Si arcus quilibet pofitìone datm A B fub-
tendatur chorda AB, & in puntto
aliquo A, in medio curvatura continua,
tangatur a retta utrinque produtta
A D i dein puntta A, B ad invicem R
ac cedant & eoe ant \ dico quod angulus
B A D , fub chorda & tangente conten-
tus, minuetur in infinitum. & ultimo e-
vanefeet.
Nam fi angulus ille non evanefeit, continebit arcus A B cum tangente
L i b E t
Primus.
A E ) angulum rettilineo aqualem, & propterea curvatura ad
ad punttum A non erit continua, contra hypothelm.
l e m m a VII.
lifdem pofitis 5 dico quod ultima ratio arcus, chorda, & tangentis
ad invicem e f i ratio aqualitatis.
Nam dum punttum B ad punttum A accedit, ìntelhgantur femper
A B & AE> ad puntta longinqua b ac d produci, & lecanti d j j
parallela agatur bd. Sitque arcus A b femper fimihs arcui A B .
Et punttis A , B coeuntibus, angulus dAb, per Lemma fuperius,
evanefeet; adeoque retta: femper finita A b , A d &c arcus ìnterme-
dius A b coincident, & propterea aquales erunt. Unde: òt hilce
femper proportionales retta A B , A E ) , & arcus mtermedius A B