i»e Moru ftum conicum ulterius d e g f in fuperficie de, & hoc fruftum
Corcorum. urget fruftum proximum f g i h in fuperficie/^, & fruftum illud
urget fruftum tertium, & fic deinceps in infinitum j manifeftum
eft (per motus Legem tertiam) quod fruftum primum defg, reazione
frufti iècundi fg h i , tantum urgebitur & premetur m fuperficie
fg , quantum urget & premit fruftum illud fecundum"
Fruftum igitur degf inter conum A d e & fruftum f h i g com-
primitur utrinque, & propterea (per Corol. 6. Prop, xix .) fig u".
ram fuam fervare nequit, nifi vi eadem comprimatur undique.
Eodem igitur ímpetu quo premitur in iuperficiebus de, fg , cona-
bitur cedere ad latera d f eg-, ibique (cum rigidum non f i t j fed
omnímodo Fluidum) excurret ac dilatabitur, nifi Fluidum am-
biens adfit, quo conatus ifte cohibeatur. Proinde conatu excur-
rendi, premet tarn Fluidum ambiens ad latera df, eg quam fruftum
f g h i eodem impetu; & propterea preflio non minus propagabi-
tur a lateribus d f eg in fpatia N O, K L hinc inde, quam pro-
pagatur a fuperficie f g verfus T Q E. D.
P R 0>
P R I N C I P I A m a t h e m a t i c a ;
p r o p o s i t i o x l i i . t h e o r e m a x x x i i i .
Motus omnis per Fluidum propagata divergit a recto tramite
in fpatia immota.
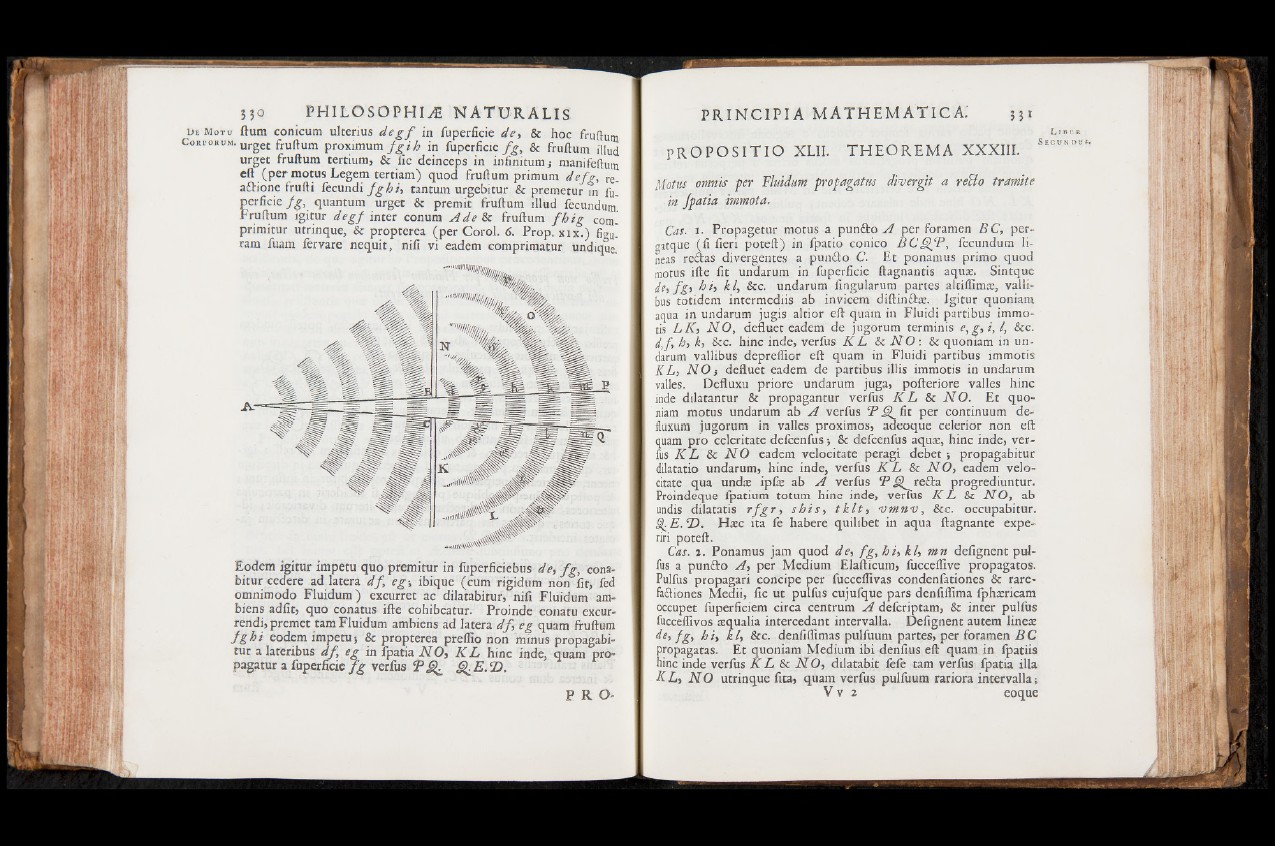
Cas. x. Propagetur motus a punZo A per foramen BC, per-
gatque (fi fieri poteft) in fpatio conico BCQfP, fecundum li-
neas reZas divergente» a punito C. Et ponamus primo quod
motus ifte fit undarum in fuperficie ftagnantis aqua:. Sintque
de, fg, hi, kl, &c. undarum fingularum partes altiflìrnsc, valli-
bus totidem intermediis ab invicem diftinZse. Igitur quoniam
aqua in undarum jugis altior eft quatn in Fluidi partibus immo-
tis LK, NO, defluet eadem de jugorum terminis e,g,i , l, Sec.
df, h, k, Sec. hinc inde, verfus K L Se N O : Se quoniam in undarum
vallibus depreftior eft quam in Fluidi partibus immotis
KL, N O -, defluet eadem de partibus illis immotis in undarum
valles. Defluxu priore undarum juga, pofteriore valles hinc
inde dilatantur & propagantur verfus K L Se N O . Et quoniam
motus undarum ab A verfus T S fit per continuum de-
fluxum jugorum in valles proximos, aaeoque celerior non eft
quam prò celeritate defeenfus s & defeenfus aquae, hinc inde, verfus
K L Se N O eadem velocitate peragi debet -, propagabitur
dilatatio undarum, hinc inde, verfus K L Se N O , eadem velocitate
qua undas ipfe ab A verfus F J / reZa progrediuntur.
Proindeque fpatium totum hinc inde, verfus K L Se N O , ab
undis dilatatis r fg r , shi s , t k l t , vmnv , Sec. occupabitur.
Qi E . cD . Haec ita fe habere quilibet in aqua (lagnante expe-
riri poteft.
Cas. 2. Ponamus jam quod de, fg, h i, kl, mn defignent pul-
fus a punZo A , per Medium Elafticum, fucceflive propagatos.
Pulfus propagari concipe per fucceifivas condenfationes & rare-
faftiones Medii, fic ut pulfus cujufque pars denfifiima fphxricam
occupet fuperficiem circa centrum A deferiptam, & inter pulfus
fucceflivos atqualia intercedant intervalla. Defignent autem linea:
de, fg , h i, kl, Sec. denfilììmas pulfuum partes, per foramen B C
propagatas. Et quoniam Medium ibi denfius eft quam in fpatiis
hinc inde verfus K L Se N O , dilatabit fèfe tam verfus fpatia illa
K L , N O utrinque fita, quam verfus pulfuum rariora intervalla ;
V v 2 eoque
LlU ER
Secundu*.
p