11
11
illlBI.
De
C or
Mom ut velocitas & pars altera ut
r0RUM velocitatis quadratum, fit re-
fiftentia tota in P ut A P quad
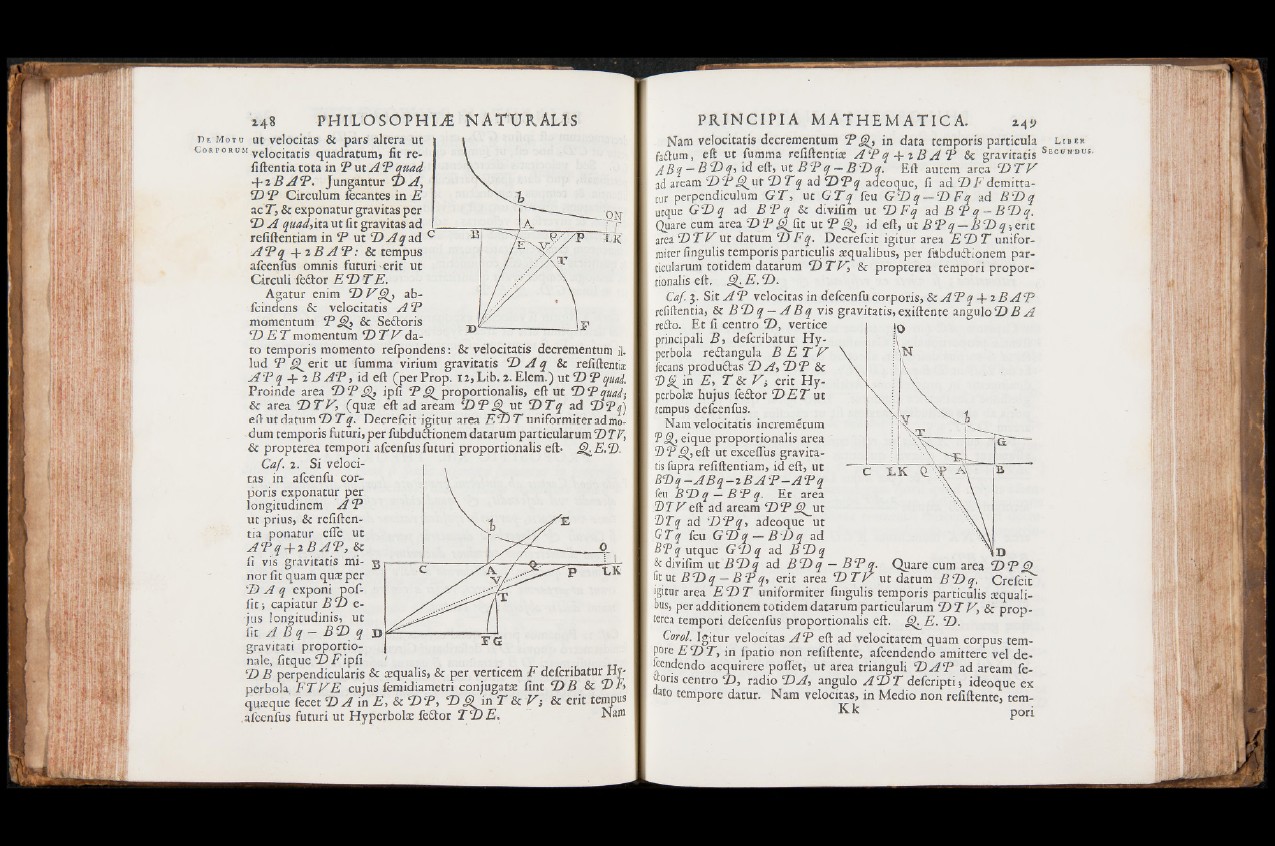
+ 2B A P . Jungantur D A ,
D P Circulum fecantes in E
ac T, & exponatur gravitas per
D A quad,ita. ut fit gravitas ad
refiftentiam in P ut DA q a d
A P q -f 2B A T : Se tempus
afeenfus omnis futuri erit ut
Circuii feétor E D T E.
Agatur enim D V^T, ab-
fcindens & velocitatis A P
momentum P Q Se Se&oris
D E T momentum D T V dato
temporis momento refpondens : & vélocitatis decrementum ¡].
lud P F f erit ut fumma virium gravitatis D A q & refiftentis
A P q -f 2 B A P , id eft (per Prop. i2,Lib. 2. Elem.) ut D P quad.
Proinde area D P Gf, ipfi P @ proportionalisj eft ut D P quad-,
Se area D T V , (qux eft ad aream © P i ? ut D T q ad D P if]
eft ut datum DT q . Decrefcit igitur area E D T uniformiter ad mo-
dum temporis futuri, per fubdu&ionem datarum par ticularum DTV,
Se propterea tempori afeenfus futuri proportionalis eft* M±E.P.
Caf. 2. Si velocitas
in aiceniu corporis
exponatur per
longitudinem A P
ut prius, & refiften-
tia ponatur eile ut
A P q + ì B A P , Se
fi vis gravitatis minor
fit quam qua: per
D A q exponi pof-
fitj capiatur B D e-
jus longitudinis, ut
fit A B q — B D q
gravitati proportionale,
fitque D F ipfi
D B perpendicularis & mqualis, & per verticem F deicribatur Hy-
perbola F T V E cujus femidiametri coniugata: fint D B Se D F
queeque fecet D A rn E, Se D P , D D i n T & Vi Se erit tempus
.afeenfus futuri ut Hyperboke fedor T D E . Nani
Nana velocitatis decrementum P J ( , in data temporis particula
faftum, eft ut fumma refiftentia: A P q + t B A P Se gravitatis
jB q — B D q , id eft, ut B P q — BD q . Eft autem area D T V
aream D P ^ f n t D T q ad D P q adeoque, fi ad ©Pdemitta-
tur perpendiculum G T , ut GTq feu G D q — D F q ad B D q
utque G D q ad B P q Se divifim ut D F q ad B P a - B D q .
Quare bum area D P QJit ut P £>, id eft, ut B P q — BDq- ,ent
area D T V ut datum D Fq. Decreicit igitur area E D T uniformiter
fingulis temporis particulis atqualibus, per fubdudionem par-
ticularum totidem datarum D T V , Se propterea tempori proportionalis
eft, D^E. D .
Caf. 3. Sit A P velocitas in defeenfu corporis, SeAPq -4-2 B A P
refiftentia, Se B D q - A B q vis gravitatis, exiftente angulo D B A
redo. Et fi centro D, vertice
principali B , deferibatur Hyperbola
redangula B E T V
fecans produdas D A , D P Se
Dg^in E , T Se V i erit Hyperbola:
hujus fedor D E T ut
tempus defeenfus.
Nam velocitatis incremétum
eique proportionalis area
D P D? ut exceflus gravitatis
fupra refiftentiam, id eft, ut
B D q - A B q - l B A P - A P q
feu B D q — B P q . Et area
D T V eft ad aream © P i^ u t
DTq ad D P q , adeoque ut
GTq feu G D q — B D q ad
BP q utque G D q ad B D q
& divifim ut B D q ad B D q — B P q . Quare cum area D P 9
fit ut B D q — B P q, erit area D T V ut datum B D q . Crefcit
igitur area E D T uniformiter fingulis temporis particulis tequali-
bus, per additionem totidem datarum particularum D T V , Se propterea
tempori defeenfus proportionalis eft. D .
Corol. Igitur velocitas A P eft ad velocitatem quam corpus tempore
E D T , in fpatio non refiftente, afeendendo amittere vel de-
icendendo acquirere poffèt, ut area trianguli D A P ad aream fe-
doris centro ©, ràdio D A , angulo A D T deferiptt ; ideoque ex
dato tempore datur. Nam velocitas, in Medio non refiftente, tem-
L I B ER
S e c u n d ü s .
Kk pori
1
■ ||||H
I