.33 »8 ì
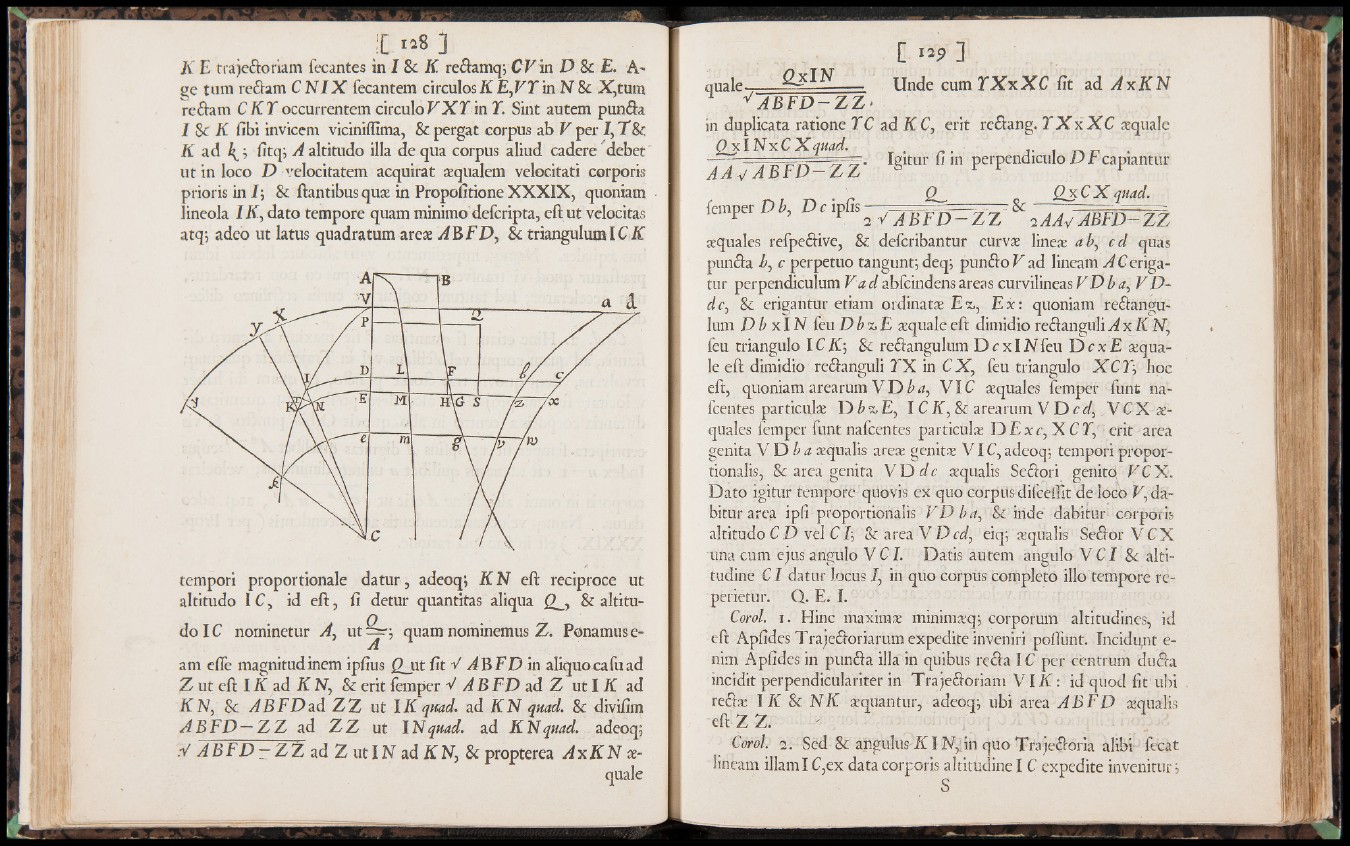
K E trajeiloriam fecantes in I Se K. reilarnqrCEin D & E. A-
ge turn reitam C N I X fecantem circuiosK E,VYin N Se X,tum
reilam C K Y occurrentem circuloV X Y in Y. Sint autem punita
I Se K fibi invicem viciniifima, & pergat corpus ab V per I, T Se
K ad fitq; A altitudo illa de qua corpus aliud cadere debet
ut in loco D velocitatem acquirat æqualem velocitati corporis
prioris in I; Se ftantibusquæ in Propofìtione XX XIX, quoniam
lineóla IK , dato tempore quam minimo deferipta, eft ut velocitas
atq; adeò ut latus quadratum areae A B FD , Se trìanguIumlCA
tempori proportionale datur, adeoqj K N eft reciproce ut
altitudo I C, id eft, fi detur quantitas aliqua & altitudo
IC nominetur A. ut^=", quam nominemus Z . Ponamuse-
A
am effe magnitudinem ipfius 2_ut fit V Àft FD in aliquota fu ad
Z ut eft I l i ad K N, Se erit femper V AB F D ad Z ut I K ad
Ì N , & ABFDa d Z Z ut I Kqmd. ad K N qmtd. Se divifim
A B F D — Z Z ad Z Z ut I Nquad. ad KNquad. adeoq;
.V A B F D — Z Z ad Z ut IN ad K N } Se propterea A x K N xquale
quale. ^ I N — Unde cum Y X x X C fît ad A x K N
V A B F D - Z YC Z ‘
in duplicata ratione ad KC, erit reif ang. Y X x X C æquale
^ ¿ Z * Igitur fi in perpendículo DFcapiantur
■ H „ QxC X quad.
femper Db. De ìpfis — ------------------- F , F 2 ~ Se -—;—— æquales refpe&ive, & Vde AfeBribFàDnt u—r ZcuZr væ aÜAneAæv A B F D - Z Z ab, cdpunita, quas b, c perpetuo tangunt; deq; punilo V ad lineam A Ctur perpendiculum eriga- Va d abfeindens areas curvilíneas VD b a, VD-
dc, 8e erigantur etiam ordinatæ Ex, Ex:lum quoniam reitangu- D b x IN feuDb %, E æquale eft dimidio reilanguli A x Kfeu triangulo I N,CX; Se reilangulum DcxINfeu DcxEle eft dimidio reilanguli TX in C X, feu triangulo acquaXCY)
eft, quoniam arearum VD hoc ha,feerites particulæ D VI6' æquales femper flint na- b % E, I C K, Sequales femper funt nafeentes particul æar eDarum VDci, VCX aeExc,
genita VD XCF, erit area hationalis, æqualis areæ genitæ VIC,adeoq; tempori propor- Se area genita V D d c æqualis Scolori genito Dbitautro airgeiatu rip tiel mprpoopfoérqcuióonv aisl i se x quo corptìs diféèffit de loco VFC,dXa.- VD ba, Sealtitudo inde dabitur corporis CD vèl CE, Se area VDcd,una cum ejus ángulo eiq; æqualis Seilor VCX V C L Datis autem ángulo VCI 8etudine altiCI
datur Lócus I,perietur. Q. E. I. in quo corpus completo ilio tempore re- Corol.eft Apfid eis. THrainjeci lomraiaxrimumæ emxpineidmitæeq i;n vceonrpiroi rpuomff unatl.t itIundciindeusp, t ied- innimcid Ait ppfeidrpese nind icpuulnarititae ril lian inT rqaujiebiulos rriaenilia VICI Ape:r icde nqturuomd fditu uilbai reilæ IK Se NK æquantur, adeoq; ubi area A B FD eft Z Z. æqualis Corol. 2. Sed Selineam illamIC,ex d aantag cuoIrupsoXriIsN a,l;tiintù dqiunoe TI rCa ejexiploerdiiat ea ilnibvei nfietcuarti S