[ 2 p 8 ]
areae E eqQ, EeaA aequales, Sc inde areae his proportionales
Tmt Z , Xh mTetiam aequales & lineae bX, ST, S Z ideft AH,
E M, O l continue proportionales, ut oportet. Et fi lineae S A,
S E, b£>_pbtinent alium quemvis ordinem in ferie continue pro-
portionalium, lineae AH, EM, (?T, ob proportionales areasHy-
perbolicas, obtinebunt eundem ordinem in alia ferie quantitatum
continue proportionalium.
Prop. XXII. Theor. XVI.
Sit Eluidi cnjufdam den fit as comprefßoni proportionalis, &• partes
ejm a gravitate quadratis dißantiarum fuarum a centyo reciproce
proportionali deorfnm trahantur : dico quod ß dißantid fumantur in
progreffiom Mnfica, denßtates Eluidi in his diflantik erunt in pro-
greffioneGeometrica. ,
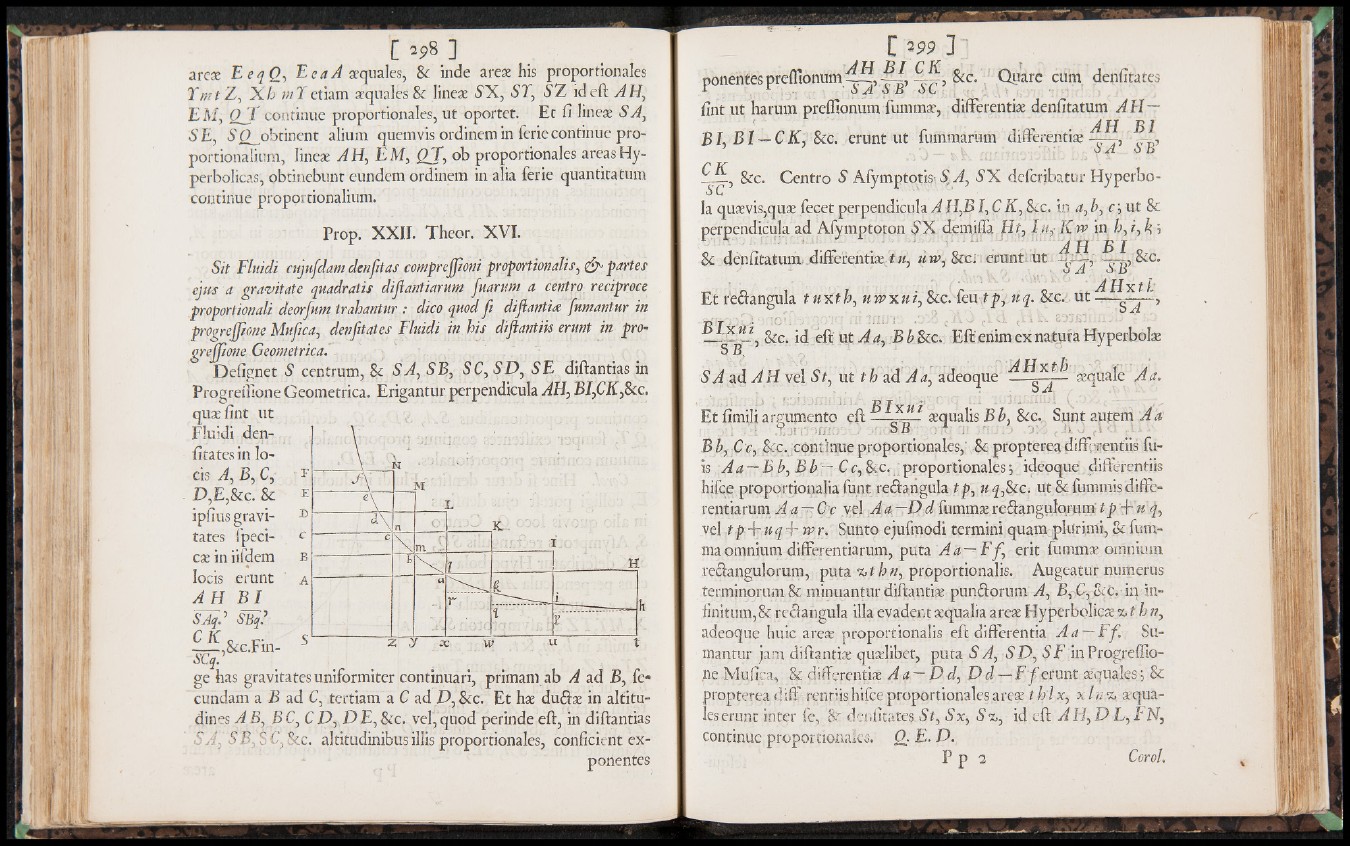
Defignet S centrum, 8c SA, SB, SC,SD, SE diftantias in
Progreillone Geometrica. Erigantur perpendicula AH, BI,CK,Sic.
quaefint ut
Fluidi den-....
iitates in lo-
cis A, B, C,■
D,E,Scc. Sc E
ip fiu s g r a v i- 15
ta t e s fp e c i- c
cae in iifd em b
lo c is e r u n t a
A U BJ.
SAq. | SBq?
— ,Scc.¥m- s
SCq.
ge has gravitates uniformiter continuaff, primam ab A ad B, fe-
cundam a B ad C, tertiam a C ad D,Sic. Et hae dudae in altitu-
dines AB, BC,CD, , DE , See. vel,quod perinde eft, in diftantias
SA, SB: 8 C, Sic. altitudinibus illis proportionales, conficient exporientes
C W ]
ponentes See.'' Qiiare cum, denfttates
fint ut harutn preifionum fummae, differentiae denfitatum A H —
BI, Bl~~CK, Sic. -erunt ut fummarum differentiae 4 ^ ,
c>/\ fft o A ^ v Jj
^ , Sic. Centro «S' Afymptotisi $A, bX deferibatur Hyperbola
quaevis,quae fecet per pendicula A H,B I, C K , Sie. in a, b, c\ ut Sc
perpendicula ad Afymptotpn $X demiffa Ht, bUrn a Itt,- Kw in h, i, k > ■ F» m&mqxii nt uji a uran B l
Sc denfitaiumj difFerehtiae/i^ u w, . ie- tunti süt Jö® w— , Scc. ' > , \ y **■ fl Iyi. JJ x t / *
Et r'edangula t nx f h, nwxui , Sic.Ecu tp, uq. Sccc,ut . -
id eft ut Aa, B bSzc. Eflieriim ex natura Hyperbolae
S J3,
SA ad A II vgl St, ut th ad A a, adeoque ^ ~ sequale Aa.
■ II TJ T:y ' ''** ' ‘ ■ "• : ■
Et fimili argujnento eft — 1 aequalis B b, See. Sunt aufem A d'
■ a n i? rrio 3 x J ' S B )■;>; 'i r :.''i i ;:» c A o C1 u <yi v
proportionales,: & propterea diftc®enti;is fu-
is :Aa — B b, B b — Cc, & cfi: proportionales j idepque, diflbrentiis
hifee proppjrtionalia funt reftangula tp, u q,Scc. ut & fummis difte-
rentiarum A a — C°c vpl A a~D d fummx reftangulprum' t p A uß,
vel .tpA- uqdr wr. SuUto ejufmodi termini quam pkfrimi, & fum-
ma pmnium differentiarum, puta_ A ä — F f , erit fummae omnium
redangulorum, puta %> t h n, prppottionalis. Augeatur numerus
teiminorum & minuantur diftantiäe pundorum^ A, B^C,ßcc,-in infinitum,&
redangula illa evadent sequalia arese Hyperbpliese % t h n,
adeoque huic areae proportionalis eft differentia A a —Ff. Su-
mantur jam diftantiae qualibet, puta S A, SD, SF in Progreffio-
,ne Mufica, 8c differentiae Aa — Dd, D d — F f erunt aequales j Sc
propterea diff rent:is hifee proportionales areae t h l x, x l k ^ aequales
erunt inter fe, & denfitates bi, Sx, S %, id eft AH,D L , FN,
continue proportionales. O. E. D.
P p 2 Corol.