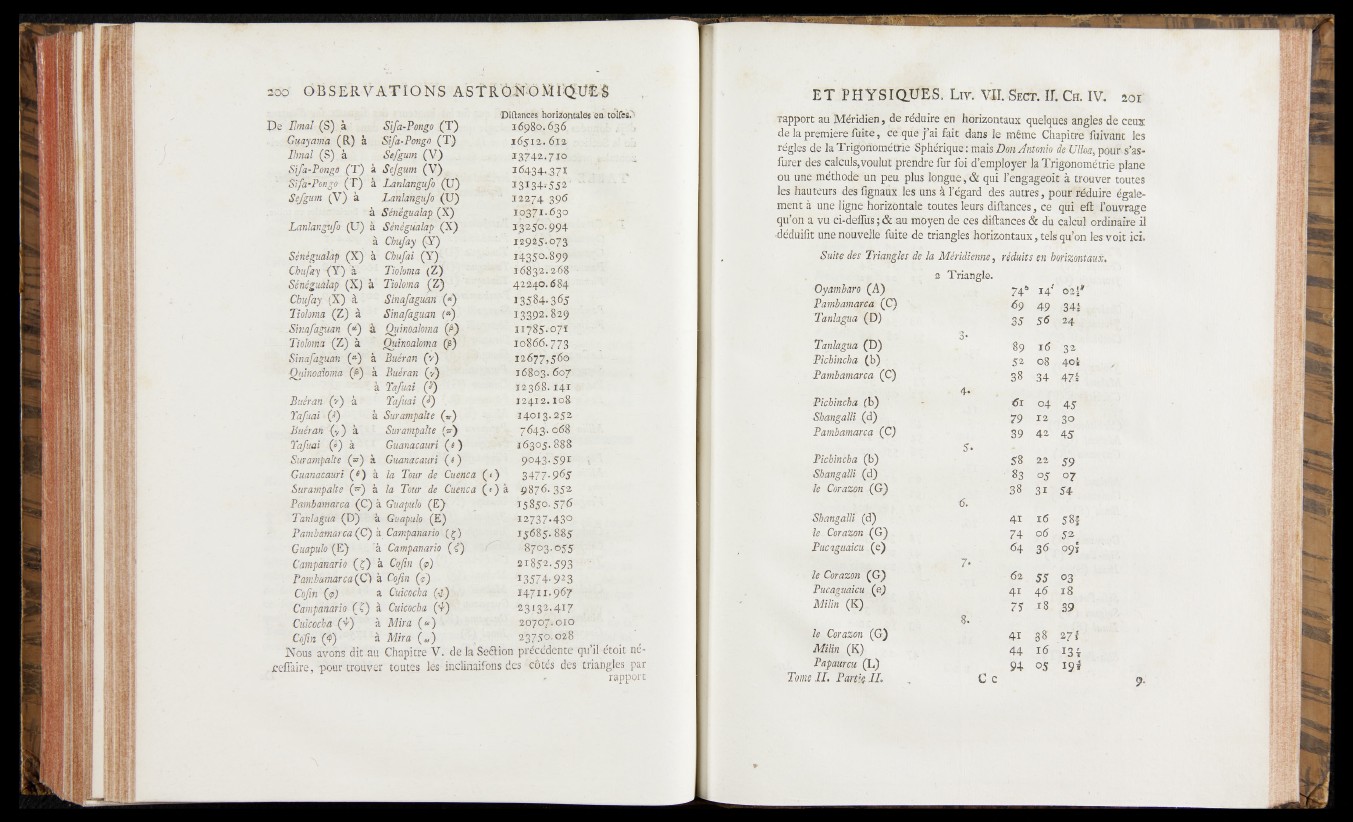
J5e limai £S) à fc Sÿa~Pongo {T )
Guayama (R) à Sifa-Pongo (T)
limai (S), à Stfgum (V)
Sfa-PongO .(T) à Sejgum (V ) t
- SififPongè'- ('T) à Lanlangufo (U)
Sejgum (V) à LanlàngUjo (Ù)
à Sénëgualap (X)
Lanlangufo (t?) à Sénégualaffâ)
à Chufay (T)
Sènèguaïap (X) à Chufai (Y )
£ h u fa y fT )& ^ - Tioloma (Z j
Sènèguàlap (X) à Tioloma (Z) .
Chufay}$£) -à - - SinafagUartf'*)
Tioloma (Z ) à
Sinafaguan (f)
Sinafagmn (*)
Tioloma (Z ) à
â, Quinoaloma (g)
Quinoaloma (|)
Sinafaguan if) ' à Buéran (y)
Quinocdoffta (f) à Buéran (?)
à Tafuai. (*)
Üiftîtfcès horijfqhtalës eU tûîfes.''
... i(598pi$36t^i,r;r;c.i jfâfc
16512..6J2
. ÏS742-7IO i , ; . . s,
• 16434^7^ ^
13*34*55^ ■
'? 1^ 7 4 "39<5
^ 7 1 .^ 3 0
— 1325&P94 .
g r2 p i5 lè | f •-
■ 1-4350.8I9-
'--42240.684
'13584.365
•y 1*339-21829
11785.-07T
12677,560-
' 16éo|v}5o7;
5? i23jf$. 141 ;*
| ", i24Ï;?, 10.8
| 44013.252
ËÉÊ|§É 068 ■
W:
5 -9®4$%9r • I I
BuèrarùXv) à : T afm iff) (•#
•. Tafuai à Surampalte (»)
Buéraê^y & 1 Surampalte rf )
Tafuai •(?) à Guanacauri (a)
Surampalte à Guanacauri (.t'y
Guanacauri ( t ) à & Toar de Cuenta ’(«,)
^ 471.965 Pf
Surampalte ( f ) à rai Tour de Guette d (*) à
9876- 352
Pambamarea (C f k Guapulo (E)
i 585o- 576 ,
Tanlagtid (D) 1 % Guapulo (E)
-* 273 7-43P. jj
PamhamaroàfCS) k Campanàmo\(g)
r5685. j 85
GuapüloHJG) - - 1 ’-k Campanario
^ © 3.^55
GampdnaHd (ÿ) à &jfï» -
2185^)5’9àv^
Tambamarca(C)kCofin (0) ■
^357^ 9^-3 . |
;• 1 : a CuMcha:(y)
Campdttârib\^J) i CM&cki (4)
g jg Cüitoâu ( 4) à Mira (<*} &>
' ■ €0#». ^ jC>- '•‘ '•à Üfhr ( # )- " ’•
2'3:7.5Q.; é$8’
Nous avons die au Chapitre V. deJaSeépon précédenre ^u’iMtoit né-
■ ppïïairpj pour trouver toutes les inclinaisons des *cétés des triangles par
- • | • - , ,■* rapport
rapport au "Méridien, de réduire en horizontaux quelques angles de ceux
de la premiérefuité, âë*!qué'fai fait dans-le même Chapitré-fuivant les
réglesde-la Tn'gOifom'eÉhe S^heriqueï: mais D^Antonio déàülha, poufts’as-
furer des calculs,Voulut'prehdre fur foi d’employer la Trigonométrie plane
ou unesShéthodë^un peu plus longu&y& qui l’engageait à trouver , toutes
les-Hauteurs des ÏIgnaüx. les uns ^l’égard' des autres, pou^duire également
à une ligne horizontale toutes leurs diftanceS, ce qùi efl: l’ouvrage
qu’dn a vu ci-defljis ; & .au mbyen dè^cés ^iftances & du calcul ordinaire il
déduifit une nb'uv'dlé^ fuite de trianglestiorizontauX, tels qu^'bn les-voit ici.
Suite des Triangles "fl? la Méridienne-, réduits en horizontaux! *
Oyamhafo\A)
* 2 Triangle.
744 14^ 021*
Pambama0aj: (C) \ 49; ;341
Tanlaguâ -(D) '"35 . 56 H :
3*
Tanlagua (D)
89 ",'32
Pichmcjiâ (b)-' 54 40*
Pambàmarca. (0) 38 «34'' 47f !
. 4*
PicMncha. (b)
H ■ '4p
Shangalli .(d) , 79 .I 2tv,30, „
Pambamarca (C ) ■ 39 42 45
5*
Pichmchaffy ’
58 22 s '59 41
Shangalli (d} •*83 H 07 j
le Corazon (G) 38 /34| 54
& r
Shangalli (d)
41 16 58f
Je . Corazon (G) , W ,06 ,pipi
Pucaguaicu ,:(e), ’ 64 091
| 7»
le Corazon "(G)
-6a; 55 o t ‘J
PucaguaicuA®), i 4 î ‘ ;M 18 1
Milin (1^5%.^^
8.
' 75 ,3 9 ,
le Corazon (G) 41 ü 27^v
Miin Ç(K) 44 l6-r i.3 i
Papaurcu (L) 9+ 05 19#
? IJ. Part# IL , Ce