| H A
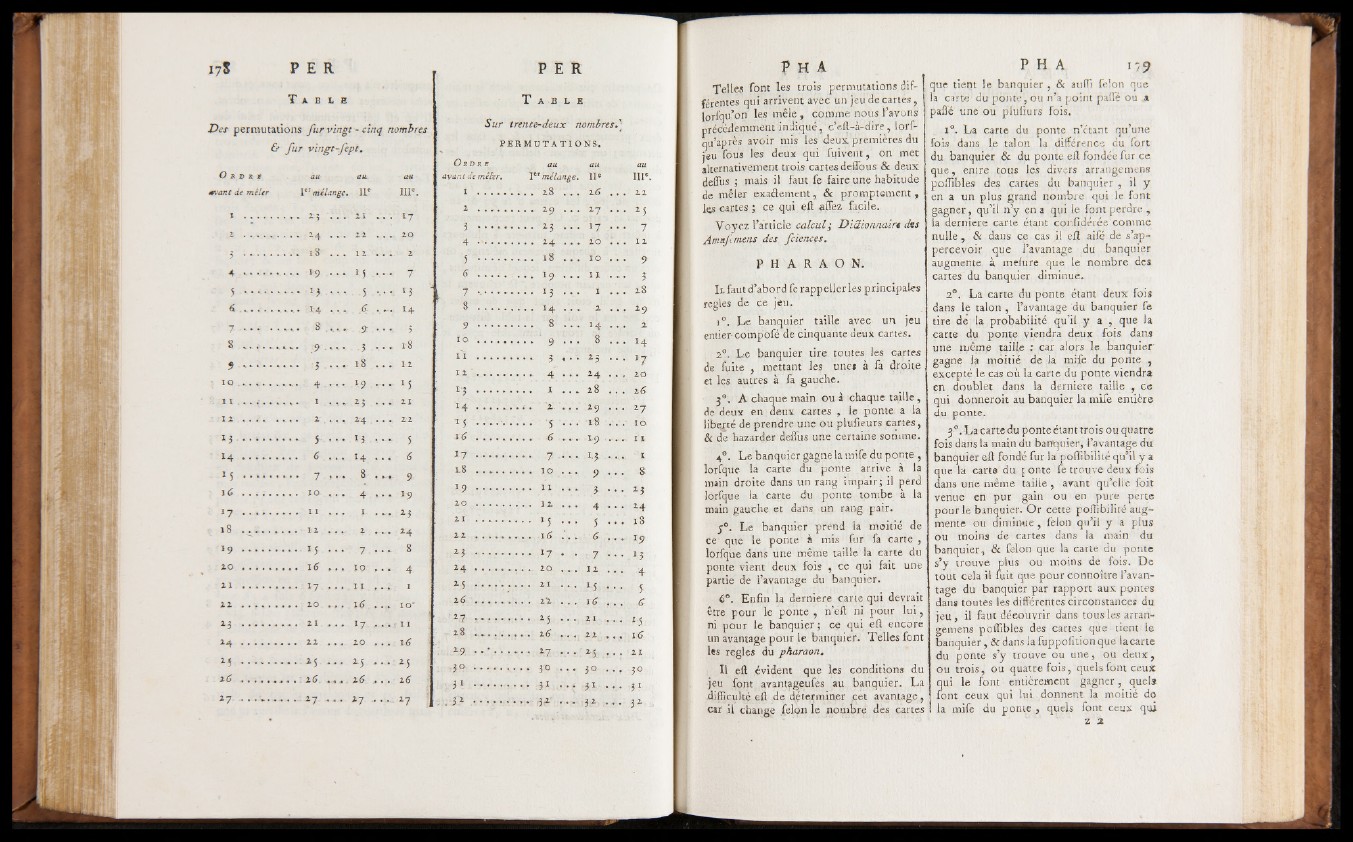
Telles font les trois permutations différentes
qui arrivent avec un jeu de cartes,
lorfqu’on les mêle, comme nous l’avons
précédemment indiqué, c’eft-à-dire, iorf-
qu’après avoir mis les deux premières du
j«u fous les deux qui fuivent, on met
alternativement trois cartes deffous & deux
deflus ; mais il faut fe faire une habitude
de mêler exadement, & promptement,
les cartes ; ce qui eft allez facile.
Voyez l’article calcul ; Diàionnairt dts
Amuf.mens des fciencçs.
P H A R A O N .
Il faut d’abord fe rappeilerles principales
réglés de ce jeu.
i°. Le banquier taille avec un jeu
entier-compofé de cinquante deux cartes.
2°. Le banquier tire toutes les cartes
de fuite , mettant les une» à fa droite
et les autres à fa gauche.
j a. A chaque main ou à chaque taille,
de deux en deux cartes , le ponte a la
liberté de prendre une ou plufieurs cartes,
& de hazarder deflus une certaine somme.
4°. Le banquier gagne la mife du ponte,
lorfque la carte du ponte arrive à la
main droite dans un rang impair; il perd
lorfque la carte du ponte tombe à la
main gauche et dans un rang pair.
y°. Le banquier prend la moitié de
ce que le ponte à mis fur fa carte,
lorfque dans une même taille la carte du
ponte vient deux fois , ce qui fait une
partie de l’avantage du banquier.
6°. Enfin la derniere carte qui devrait
être pour le ponte , n’eft ni pour lu i,
ni pour le banquier ; ce qui eft encore
un avantage pour le banquier. Telles font
les réglés du pharaon..
Il eft évident que les conditions du
jeu font avantageufes au banquier. La
difficulté eft de déterminer cet avantage ,
car il change félon le nombre des cartes
P H A 179
que tient le banquier , & aufïi félon que
la carte du ponte , ou n’a point paflé ou a
paflé une ou plufiurs fois.
i°. La carte du ponte n’étant qu’une
fois dans le talon la différence du fort
du banquier & du ponte eft fondée fur ce
que, entre tous les divers arrangemens
poftîbles des cartes du banquier , il y
en a un plus grand nombre qui le font
gagner, qu’il n’y en a qui le font perdre ,
la derniere carte étant corfidérée'comme
nulle , & dans ce cas il eft aifé de s’ap-
percevoir que l’avantage du banquier
augmente à melure que le nombre des
cartes du banquier diminue.
2°. La carte du ponte étant deux fois
dans le talon , l’avantage du banquier fe
tire de la probabilité qu’il y a , que la
carte du ponte viendra deux fois dans
une même taille : car alors le banquier
gagne la moitié de la mife du ponte ,
excepté le cas où la carte du ponte viendra
en doublet dans la derniere taille , ce
qui donneroit au banquier la mife entière
du ponte.
3°.La carte du ponte étant trois ou quatre
fois dans la main du banquier, l’avantage du
banquier eft fondé fur la polîibilité qu’il y a
que la carte du fonte fe trouve deux fois
dans une même taille , avant qu’elle foit
venue en pur gain ou en pure perte
pour le banquier. Or cette poftibilité augmente
ou diminue , félon qu’il y a plus
ou moins de cartes dans la main du
banquier, & félon que la carte du ponte
s’y trouve plus ou moins de fois. De
tout cela il fuit que pour connoître l’avantage
du banquier par rapport aux pontes
dans toutes les différentes circonstances du
jeu, il faut découvrir dans tous les arrangemens
poflibles des cartes que tient le
banquier, & dans la fuppofitionque lacarte
du ponte s’y trouve ou une, ou deux,
ou trois, ou quatre fois, quels font ceux
qui le font entièrement gagner, quel*
] font ceux qui lui donnent la moitié de
t la mife du ponte , quels font ceux qui
z 2