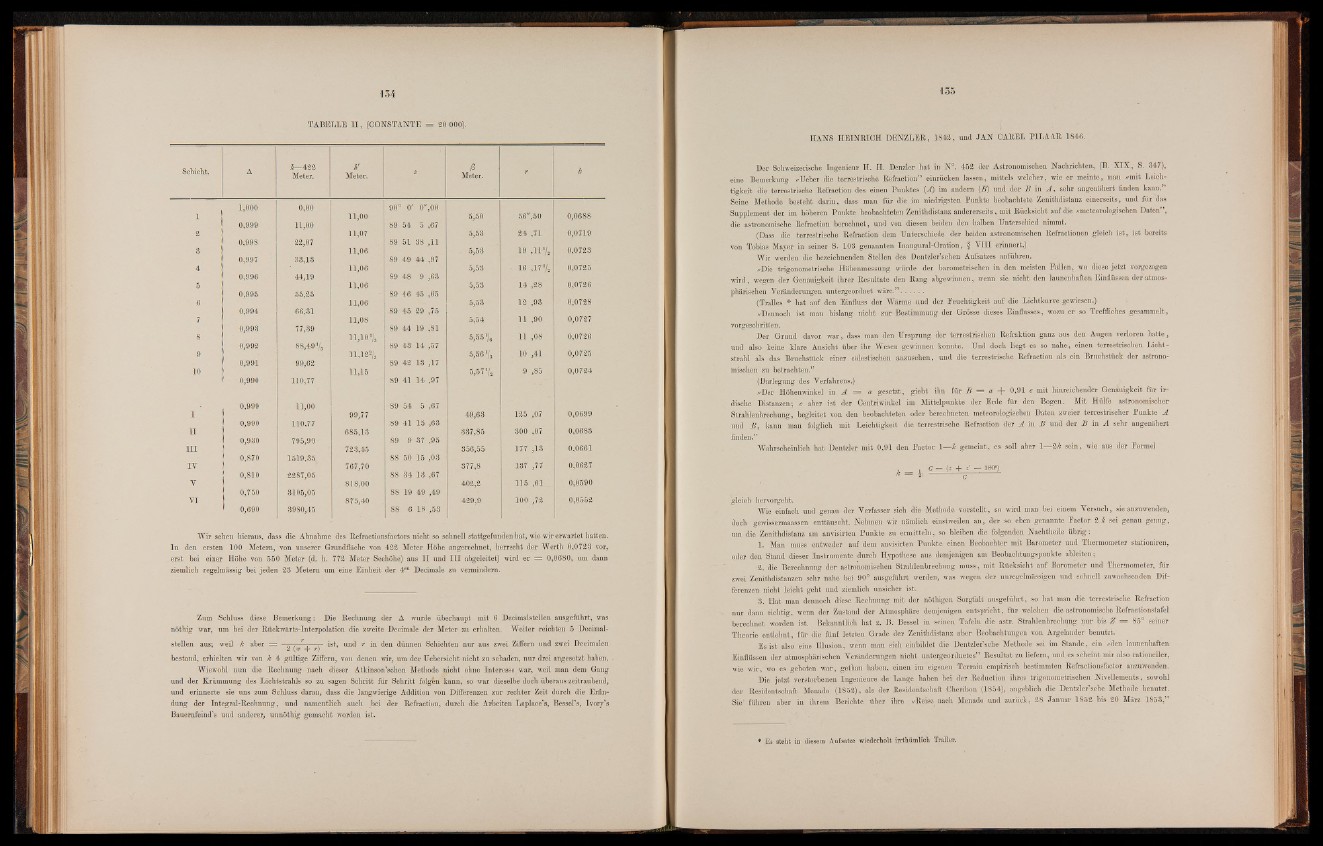
Schicht. A A—422
Meter.
h!
Meter.- «
ß
Meter. - k
l ,O 0 t $ \ 0 ,0 0 + ' 90° 0' 0W,00
1 I 11,00 5,50 56",50 ' 0,0688-
0,999 11,00 89 54 5 ,67
2 11,07 ' 5,58 24 ,71 0,0719
0,998 22,07 89 51 88 ,11
3 11,06 - 5,53 19 ,Vt% 0,0723
0,997 38,18 . 89 49 44 ,97
4 11,06 5,58 j@ $ 6 ,17 '/2; 0,0725
. 0,996 44,19 89 48 9 ,68
5 ’ 11,06 5,53 14 ,28 0,0726
* 9 9 5 , „¿55,25 89 46 45 ,65
6 1+0:6 ' 5,53 12 ,93 0,0728
-"A 0,994 66,31 89 45 29 ,75
7 11,08 5,54 - ’11 ,90 .. 0,0727
0,993 77,39 89 44 19 ,81
8 llj lO ’/s 5,55 V6 11 ,08 0,0726
0,992 88,49 7a 89 43 14 ,57
9 l l ,1 2 2/3 5,5673 10 ,41 l.Ö>0725
0,991 99,62 89 42 13 ,17
10 11,15 5,57 Vj 9 ,85 . 0,0724
0 ,9 9 |§ || 110,77 89 41 14 ,97
0,999 11,00 89 54 5 ,67
... I 99,77 49,63 125 ,07 0,0699
0,990 110,77 .89 41 15 >68
n 685,13 337,85 800 ,07 0,0683
0,930 795,90 ' ' 89 9 37 ,95
m 723,45 356,55 177 ,13 0,0661
+'0,870 1519,35, 88 ,50 15 ,03
IV 767,70 377,8 137 ,77 0,0627
0,810 2287,05 88 34 13 ,67
V 818,00 402,2 115 ,61+. P|P05:90
0,750 ' 3105,05 88 19 49 ,49
VI 875,40 429,9 100 ,72 0,0552
0,690 3980,45 88 6 18 ,53
Wir sehen hieraus, dass die Abnahme des Refractionsfactors nicht so schnell stattgefunden hat, wie wir erwartet hatten,
ln den ersten 100 Metern, von unserer Grundfläche von 422 Meter Höhe angerechnet, herrscht der Werth 0,0723 vor,
erst bei einer Höhe von 550 Meter (d. h. 772 Meter Seehöhe) aus II und III abgeleitet) wird er — 0,0680, um dann
ziemlich regelmässig bei jeden 23 Metern um'eine Einheit der 4en Decimale zu vermindern.
Zum Schluss diese Bemerkung: Die Rechnung der A wurde überhaupt mit 6 Decimalstellen ausgeführt, was
nöthig war, um bei der Rückwärts-Interpolation die zweite Decimale der Meter zu erhalten. Weiter reichten 5 Decimalstellen
aus; weil k aber — ^ \ ist, und r in den dünnen Schichten nur Z (io + r.) . aus zwei Ziffern und zwei Decimalen
bestand, erhielten wir von k 4 gültige Ziffern, von denen wir, um der Uebersicht-nicht zu schaden, nur drei angesetzt haben.
Wiewohl nun die Rechnung nach dieser Atkinson’schen Methode nicht ohne Interesse war, weil man dem Gang
und der Krümmung des Lichtstrahls so zu sagen Schritt für Schritt folgen kann, so war dieselbe doch überaus zeitraubend,
und erinnerte sie uns zum Schluss daran, dass die langwierige Addition von Differenzen zur rechter Zeit durch die Erfindung
der Integral-Rechnung, und namentlich auch bei der Refraction, durch die Arbeiten Laplace’s, Bessel’s, Ivory’s
Bauernfeind’s und anderer, unnöthig gemacht worden ist.
HANS HEINRICH DENZLER, 1842, und JAN CAREL PILA AR 1846.
Der Schweizerische Ingenieur H. H. Denzler hat in N°. 452 der Astronomischen Nachrichten, (B. XIX, S. 347),
eine Bemerkung -//Heber die terrestrische Refraction” einrücken lassen, mittels welcher, wie er meinte, man //mit Leichtigkeit
die terrestrische Refraction des. einen Punktes {A) im ändern |p j und der £ in Ä , sehr angenähert finden kann.”
Seine Methode besteht darin, dass man für die im niedrigsten Punkte beobachtete Zenithdistanz einerseits, und für das
Supplement der im höheren Punkte beobachteten Zenithdistanz andererseils, mit Rücksicht auf die //meteorologischen Daten” ,
die astronomische Refraction berechnet, und von diesen beiden den halben Unterschied nimmt.
(Dass die terrestrische Refraction dem Unterschiede der beiden astronomischen Refractionen gleich ist, ist bereits
von Tobias Mayer in seiner S. 103 genannten Inaugural-Oration, § VIH erinnert.)
Wir werden die bezeichnenden Stellen des Dentzler’schen Aufsatzes anführen.
//Die trigonometrische Höhenmessung würde der barometrischen in den meisten Fällen, wo diese jetzt vorgezogen
wird, wegen der Genauigkeit ihrer Resultate den Rang abgewinnen-, wenn sie nicht den launenhaften Einflüssen der atmosphärischen
Veränderungen untergeordnet wäre.” ............
(Tralles * hat auf den Einfluss der Wärme und der Feuchtigkeit auf die Lichtkurve gewiesen.)
//Dennoch ist man bislang nicht zur Bestimmung der Grösse dieses Einflusses, wozu er so Treffliches gesammelt,
vorgeschritten.
Der Grund davor war, dass man den Ursprung der terrestrischen Refraktion ganz aus den Augen verloren hatte,
und also keine klare Ansicht über ihr Wesen gewinnen konnte. Und doch liegt es so nahe, einen terrestrischen. Lichtstrahl
als das Bruchstück einer cölestischen anzusehen, -und die terrestrische Refraction als ein Bruchstück der astronomischen
zu betrachten.,‘|£v^
(Darlegung des Verfahrens.)
• //Der Höhenwinkel in A = a gesetzt, gieht ihn für B j jj a + 0 , 9 1 c mit hinreichender Genauigkeit für irdische
Distanzen; c aber ist der Gentriwinkel im Mittelpunkte der Erde für den Bogen. Mit Hülfe astronomischer
Strahlenbrechung, begleitet von den beobachteten oder berechneten meteorologischen Daten zweier terrestrischer Punkte A
und B , kann man folglich mit Leichtigkeit die terrestrische Refraction der A in B und der B in A sehr angenähert
finden."
Wahrscheinlich hat Dentzler mit 0,91 den Factor 1— k gemeint, es soll aber 1— 2k sein, wie aus der Formel
I C — (z + z H l 180°)
---------------C~ J
gleich hervorgeht.
Wie einfach und genau der Verfasser sich die Methode vorstellt, so wird man bei einem Versuch, sie anzuwenden,
doch gewissermaassen enttäuscht. Nehmen wir nämlich einstweilen an, der so eben genannte Factor 2 k sei genau genug,
um die Zenithdistanz am anvisirten Punkte zu ermitteln, so bleiben die folgenden Nachtheile übrig:
1. Man muss entweder auf dem anvisirten Punkte einen Beobachter mit Barometer und Thermometer stationiren,
oder den Stand dieser Instrumente durch Hypothese aus demjenigen am Beobachtungspunkte ableiten;
-2. die Berechnung der astronomischen Strahlenbrechung muss, mit Rücksicht auf Barometer und Thermometer, für
zwei Zenithdistanzen sehr nahe bei 90° ausgeführt werden, was wegen der unregelmässigen und schnell zuwachsenden Differenzen
nicht leicht geht und ziemlich unsicher ist.
8. Hat man dennoch diese Rechnung mit der nöthigen Sorgfalt ausgeführt, so hat man die terrestrische Refraction
nur dann richtig, wenn der Zustand der Atmosphäre demjenigen entspricht, für welchen die astronomische Refractionstafel
berechnet worden ist. Bekanntlich hat z. B. Bessel in seinen Tafeln die astr. Strahlenbrechung nur bis Z = £ 8 5 ° seiner
Theorie entlehnt, für die fünf letzten Grade der Zenithdistanz aber Beobachtungen von Argeiander benutzt.
Es ist also eine Illusion, wenn man sich einbildet die Dentzler’sche Methode sei im Stande, ein //den launenhaften
Einflüssen der atmosphärischen Veränderungen nicht untergeordnetes” Resultat zu liefern, und es scheint mir also rationeller,
wie wir, wo es geboten war, gethan haben, einen im eigenen Terrain empirisch bestimmten Refractionsfactor anzuwenden.
Die jetzt verstorbenen Ingenieure de Lauge haben bei der Reduction ihres trigonometrischen Nivellements, sowohl
der Residentschaft Menado, (1852), als der Residentschaft Cheribon (1854), angeblich die Dentzler’sche Methode benutzt.
Sie' führen aber in ihrem Berichte über ihre //Reise nach Menado und zurück, 28 Januar 1852 bis 20 März 1853,”
* Es steht in diesem Aufsatze wiederholt irrthümlicli Trailer.