Wenn wirklich ein Grund dafür besteht, dass die Anomalien bei kleinen Entfernungen grösser sind als bei grossen,
so müssten es. diese sein, zumal in einem nahezu flachen Lande, wie die Lüneburger Haide, dass die grossen Entfernungen
auch nothwendig grössere Höhen bedingen. Ich wollte deshalb auch gern die Höhen der Gaussischen Stationen kennen,
wozu es rathsam wäre, die Protokolle der Messungen einzusehen.
Herr Dr. S. Ambronn, Observator der Göttinger Sternwarte, hatte die Güte, bei der Eamilie Schering, in deren
Besitz die Originale der Gaussischen Beobachtungen sich befinden, die gewünschten Zenithdistanzen oder eigentlich Höhenwinkel
ausznziehen. Indem ich überdies noch fand, dass die Höhen von einigen der von Gauss bezogenen Stationen auf
der Karte IST0. 8 3 , 84 in Andree’s bekanntem Atlas angegeben waren, so gelang es mir bald, durch Berechnung einiger
Höhenunterschiede, alle Höhen mit einer diesem Zwecke entsprechenden Genauigkeit zu finden.
Leider ergab sich auch bei der Untersuchung der Originale, dass Gauss oder die. anderen Beobachter überhaupt
keine Notizen über Barometer und Thermometer gemacht hatten. Indem ich nun die von Gauss a. a. O gegebene
Tabelle mit den Höhen ergänze, so wird sie die folgende, wo in der letzten Spalte die Hälfte des von Gauss gegebenen
Verhältnisses, also der Refractionsfactor angegeben ist.
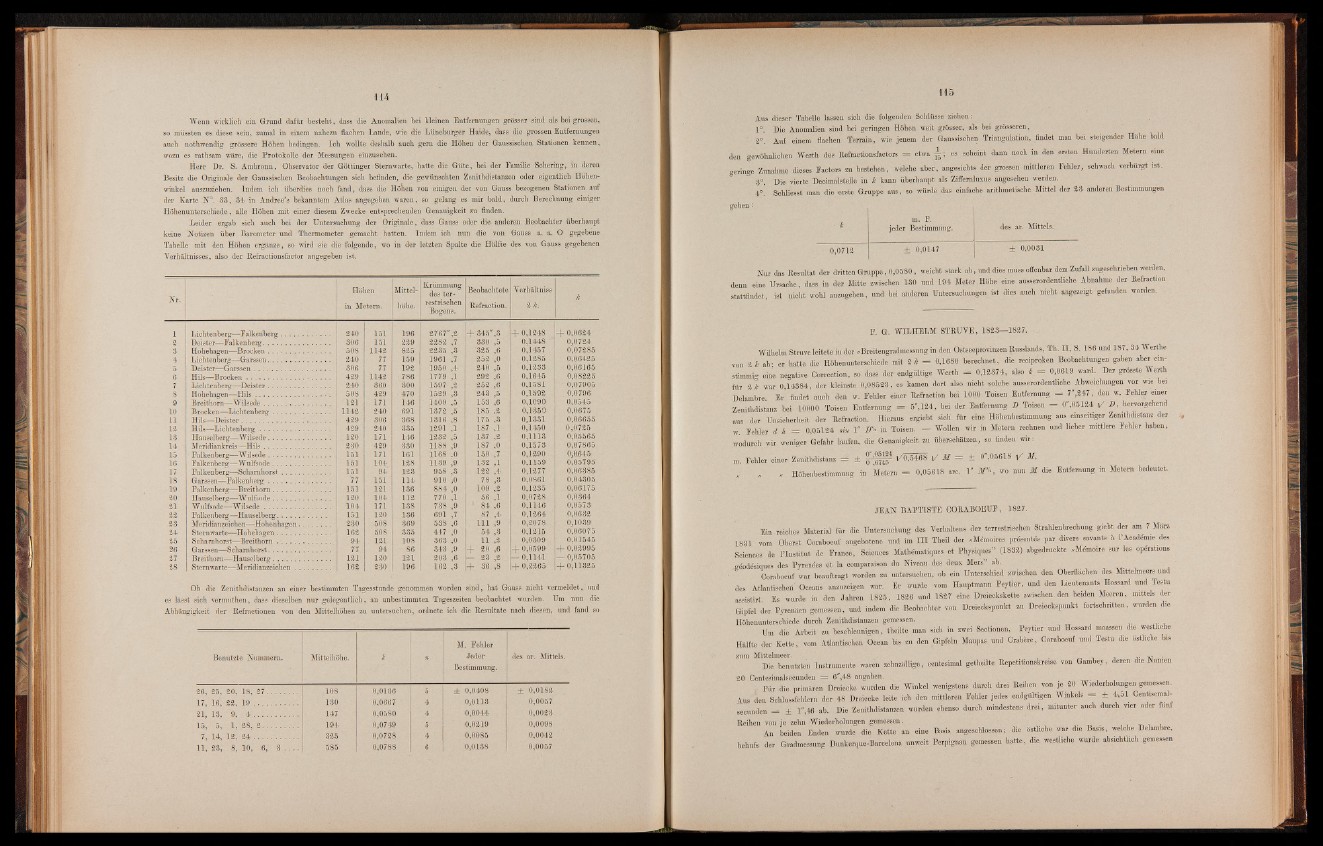
Nr.
Höhen
in Metern.
Mittelhöhe;
Krümmung
des terrestrischen
Bogens.
Beobachtete
Refraction.
Verhältniss
2 A,
1 Lichtenberg—Ealkenberg . . . . . .............. 240 151 196 2767" ,2 ||3 4 5 " ,8 + 0,1248 + I|Ö624
2 Deister—Ealkenberg............ .. . ................. 306 151 : 229 2282 ,7 880 ,5 0,1448 " 0,0724
3 Hobehagen—Brocken............. 508 1142 825 2235 ,3 '325 ,6 0,145,7 0,07285
4 Lichtenberg—-Garssen................................. 240 77 159 1961 ,7 252 ,0 0,1285 0,06425
¿ ‘¿'Sii« Deister—Garssen . . ; ................... .............. 806 77 pL 9 2 1950 ,4 240 ,5 / 0,1233 0,06165
6 Hils—Brocken .,. . . . . . . . . . . . : . . . . 429 1142 ■786 1779 ,1 292 ,6 0,1645 0,08225
7 Lichtenberg—Deister............................ .... 240 360 800/ 1597 ,2 252 ,6 0,1581 - 0,07905
8 Hohélìag'en—Hils .......................... .. 508 429 470 1529 ,3 248 ,5 : 0,1592 ; 0,0796
9 Breithorüf--Wilsede............. . 121 T 171 146 ' 1409 ,.50 153 ,6 0,1090 0,0545
10 Brocken—Lichtenberg.............. 1142 240 691 1872 ,5 185 ,2 0,1350 0,0675
.1 1 Hils—Deister . . . . . . . . . . . . . . . . . . , . 429 306 368 1316 ,8 175 ,3 0,1 3 3 Ì^ | 0,06655
12 Hils—Li chten b e r g ....................... ............. 429 240 385 1291 ,1 187. ,1 0,1450%^ 0,0725
13 Hauseiberg—Wilsede. . . . . . . . . . . . . . . 120 .0171 146 -1232 ,5 137 ,2 0,1113 0,05565
14 Meridiankreis—H ils ................... 230 429 330 1188 ,9 187 ,0 0,1573 0,07865
15 Ealkenberg—Wilsede . . ■ . . . . . . . . . . . . . 151 0 1 7 1 161 1168 .0 150 ,7 ! 0,1290 0,0645
16 Ealkenberg—Wulfsode.......................... 151 : 104 128 1139 ,9 132 ,1 0,1159 0,05795
17 151 94 123 958 ,3 122 ,4 0,1277 0,06385
18 Garssen—Falkenberg................................. '77 151 114 910 ,0 78 ,3 0,0861 0,04305
p 9 Ealkenberg— Breithorn. . . . . . . . . . . . . . ; 151 i m . 136 884 ,0 . 109 ,2 0,1235 . 0,06175
20 Hauseiberg—Wulfsode............................. 120 104 112 770 ,1Y 5,6 ,1 ‘ 0,0728 0,0364
'21 Wnlfsode-—Wilsede ................................... 104 171 138 738 ,9 1 84 ,6 0,11.46 0,0573
22 Ealkenberg —Hauseiberg............................ 15L;' 120 136 691 ,7 87 ,4 0,1264 0 ,0 6 3 2 .
23 Meridianzeichen— Hohenhagen............ 230 508 369 538 ,6 111 ,9 - 0,2078 - 0,1039
24 Sternwarte— Hohehagen ............................. 162 508 335 447 ,0Y 54 ,3 0,1215 - 0,06075
25t^ Scharnhorst—Breithom............................ 94 121 108 363 11 ,2 0,0309 . 0,01545
26 Garssen— Scharnhorst.. . . ' ................ .. 77 94 86 343 ,9 H 20 ’6 -j- 0,0599 4 - 0,02995
27 Breithorn— Hausei berg............................... 121 Ì 120 121 203 ,6 ^ „23 2 0,1141 — 0,05705
28 Sternwarte—Meridianzeichen ................... 162 230 196 162 ,3 I ti 36 + 0,2265 Ç 0 , 11325
Ob die Zenith «Distanzen an einer bestimmten Tagesstunde genommen worden sind, hat Gauss nicht vermeldet, und
es lässt sich vermuthen, dass dieselben nur gelegentlich, an unbestimmten Tageszeiten beobachtet wurden. Um nun die
Abhängigkeit der Refractionen von'den Mittelhöhen zu untersuchen, ordnete ich die Resultate nach diesen, und fand so
Benutzte Nummern. Mittelhöhe. h
M. Fehler
Jeder
Bestimmung.
des ar. Mittels.
26, 25, 20, 18, 27 . - B P 0,0136 5 ± 0,0408 ± 0,0182-
17, 16; 22, 1 9 ........................ 130 , 0,0667 4 0,0113 0,0057
21, 13, l i 4 147 0,0580 4 0,0044 0,0023
Ì5 , 5, 1, 28, 2 . ______HH 1Ö4 0,0749 0,0219 0,0098
7, 14, 12, 24 . . . . . 8 . . . . 325 0,0728. 4 0,0085 0,0042 I
11, 23, 8, 10, 6, 3 ___ 585. 0,0788 6 0,0138 0,0057
Aus dieser Tabelle lassen sich die folgenden Schlüsse ziehen:
1°. Die Anomalien sind bei geringen Höhen weit grösser, als bei grösseren,
’ 2°. Auf einem flachen Terrain, wie jenem der Gaussischen Triangulation, findet man bei steigender Höhe bald
den gewöhnlichen Werth des Eefraotions&ctors = etwa Bi; scheint dann noch in den ersten Hunderten Metern eine
j Zunahme dieses ¡Factors zu bestehen, welche aber, angesichts der grossen mittleren Fehler, schwach verbürgt ist.
3°. Die vierte DSeimalstelle in t kann überhaupt als! Ziffemluxus angesehen werden.
4Ö' Schliesst man die erste Gruppe: ans, so würde das einfache arithmetische Mittel der 23 imderen Bestimmungen
geringe .
geben:
■ h
m. E.
jeder Bestimmiing. des ar. Mittels.
0,0712 ± g | 0 l 4 7 ± 0,0031 ..
Nur' das Resultat der dritten Gruppe, 0,(Sf?0, weicht stark ab, und dies muss offenbar dem Zufall augeschrieben werden,
denn, eine Ursache, dass in der Mitte zwischen 180 und 194 Meter.Höhe eine ausserordentliche Abnahme der Refraction
stattfindet, ist nicht, wohl anzugeben, und bei anderen Untersuchungen ist dies auch nicht angezeigt gefunden worden. ■
F. G. WILHELM ST'RUVB,. 1828—1827.
Wilhelm Struve leitete in der „Breitengradmessung in den Ostseeprovinzen Russlands, Th, II, S. 186 und.187, 34 Werthe
von' 2 lt ab- er hatte die Q reciprpken Beobachtungen gaben aber einstimmig
eine negative Oorrecidoh, so dass der endgültige Werth H 0,12374, also 0,0619 ward. Der grösste Werth
für 2 h war 0,14884I der 'kleinste 0,08628, es kamen .Iprt also nicht solche ausserordentliche Abweichungen vor wie bei
Delambre Er findet auch den w. Fehler einer Refraction bei 1000 Toisen Entfernung = 7",247, den w. Fehler, einer
Zenithdistana, bei 10000 Toiseu Entfernung = -.5",124, bei der Entfernung B Toisen = 0",06124 V B , hervorgehend
aus der Unsicherheit der Refraction. Hieraus eigiebt sich' für eine Höhenbestimmung aus ..emseitiger Zemthdistanz der
"w. Fehler d /. — 0,05124 m , V lK in Toisen, — Wollen wir in.Metern rechnen und lieber, mittlere Fehler haben,
.wodmch wir,Weniger Gefahr laufen, die Genauigkeit zu überschätzen, so finden wir:
m. Fehler e i n e r ' Z e n i t h d i s t a n z V ^ m V M - * fgj§§y Jf,
• . Böhenhesidmmuiig in Metern = 0,05618 arc. 1" M'l-, wo nun M die Entfernung in Metern bedeutet.
JEAN BAPTISTE OORABOEUF, 1827.
Ein reiches Material für die Untersuchung des Verhaltens der terrestrischen Strahle,,breohung giebt der am 7 März
881' vom Oberst Coraboeuf abgebotene und im III Tlieil der „Mémoires présentes par divers savants à l’Académe des
ciencés de l’Institut de France, Sciences Mathématiques et Physique?” (1832) abgedruckte „Mémoire sur les opérations
éodésiques des Pyrenéés et la .comparaison du Niveau des deux Mers” ab.
Coraboeuf War beauftragt worden zu untersuchen, ob ein' Unterschied zwischen den OberfiSchen des Mittelmeersund
es Atlantischen* Océans anzuzeigen war. Er wurde vom Hauptmann Peytier, und. den Lieutenants Hossard und Teste
ssistirt. Es wurde in den Jahren 1825, 1826 und 1827 eine Dreieckskette zwischen.den beiden Meeren, mittels der
Mpfel der Pyrenäen gemessen, und indem die Beobachter von Dreieckspunkt zu Dreieckspunkt forteehntten, wurden die
Höhenunterschiede durch Zenithdistanzen gemessen.
Um die Arbeit zu beschleunigen, theilte man sich in zwei Sectionen, Peyt-ier und Hossard maassen die westliche
lälfte der Kette, vom Atlantischen. Ocean bis. zu den Gipfeln Maupas und Crabère, Coraboeuf und Testa die östliche bis
um Mittelmeer. _ ' ' _ ■ I , , , T •
Die benutzten Instrumente waten zehnzöllige, centésimal getheilte Repetitionskreise von Gambey, deren die Nonien
;0 Centesimalsecundeu = 6",48 augaben. .
I Für die primären Dreiecke wurden die Winkel: wenigstens durch drei Reihen von je 20 Wiederholungen gemessen,
lus den SchlussfeUern der 48 Dreiecke leite ich .den mittleren Fehler jedes endgültigen Winkels 4,51 Cenbsemalecunden
= ± 1",46 ab. Die Zeuithdistanzen wurden ebenso durch mindestens drei, mitunter auch durch vier oder fünf
leihen von je zehn "Wiederholungen gemessen. B H H B S I
An hpiden Enden wurde die Kette an eine Basis angeschlossen; die östliche war die Basis, welche Delambre,