Für jede Combination zweier Stationen hat man so viele Gleichungen dieser Art, als an denselben
Beobachtungen zu verschiedenen Tagesstunden angestellt worden sind, also für Penoenggalan-
Banjoepahit zehn, u. s. w.. Bei der Lösung wurden, der Bequemlichkeit wegen, von den Werthen von
8, U und Je, der kleinste Werth abgezogen, bevor die Anwendung der Methode der kleinsten Quadrate
Anwendung fand.
Es versteht sich, dass ich ebenso gut die Formel y B -(- S B ' hätte wählen können, es kam
mir aber vor, dass die von mir gewählte Form der Nalur der Sache mehr entsprach.
Bei dieser Lösung war aber zu bemerken, dass die Anzahl Male, dass die gegenseitigen Beobachtungen
an beiden Stationen derselben Combination gelungen sind, an den verschiedenen Tagesstunden
ziemlich verschieden sind; namentlich am Nachmittage wurden durch die aufsteigenden W^olkenmassen die
Beobachtungen manchmal gehindert; es entstand also die Frage: sollen bei der Lösung durch die
Methode der kleinsten Quadrate die Gewichte, der Anzahl der Tage proportional, an welchen die Zenilh-
dislanzen an derselben Stunde gemessen wurden, berücksichtigt werden oder nicht. Ich hatte erst die
ganze Reihe berechnet, ohne die Gewichte zu berücksichtigen, oder lieber, indem ich jedem Resultate
dasselbe Gewicht gab; später aber habe ich die Lösungen mit Rücksicht auf die Gewichte wiederholt,
um zu untersuchen, ob etwa von den vorigen abweichende Resultate herauskommen würden. Es ergab
sich, dass dies nicht der Fall war; als ich aber einen kleinen Rechenfehler berichtigte, machte ich eine
andere Erfahrung, nämlich, dass bei einer Aendcrung der Conslanten, mit welchen die ursprünglichen
8 und TJ vermindert wurden, auch die Werthe der Unbekannten, d. h. der Coefficienlen « und ß geändert
wurden.
Man wird dies leicht einsehen, wenn man bedenkt, dass die Lösung der beiden Gleichungen
8 u 4 - U ß 4 7c
8' a 4 rr ß ^ k '
zu den Resultaten führt
■,. Ü Je U Je' j n \ & &' T&iiS Je
f l ml
die, sobald man die 8 um z. B. <r vergrössert, ihren Werth verändern. Dieser Schwierigkeit ist
offenbar damit abgeholfen, dass man dem Ausdrück noch eine Constante als dritte Unbekannte hinzufügt.
Hat man nämlich
8 a, 4 TJ ß + y = Je,
8 a. 4 V ß 4 y = Je\
8 ' a 4 TJ" ß 4 y = Je",
so erhält man durch Substraction
m m ß) * + H — u ) ß = B H ■
(£" — 8) a 4 ( V ^ TJ) ß i== Je" — Je,
so dass eine Vergrösserung oder Verminderung der 8 oder der TJ um eine constante Grösse, d. h. eine
Aenderung der Zahl, von welcher ab diese Unbekannten gezählt werden, ausser Einfluss bleibt; nur die
y ändert sich, jedoch derartig, dass die Endformel dieselbe bleibt.
Ich habe also die sämmtlichen sieben Gombinalionen, welche Mittel- und Ost-Java geliefert
haben, nochmals mit Hinzufügung einer dritten Unbekannte aufs Neue gelöst und, wie auch die vorigen
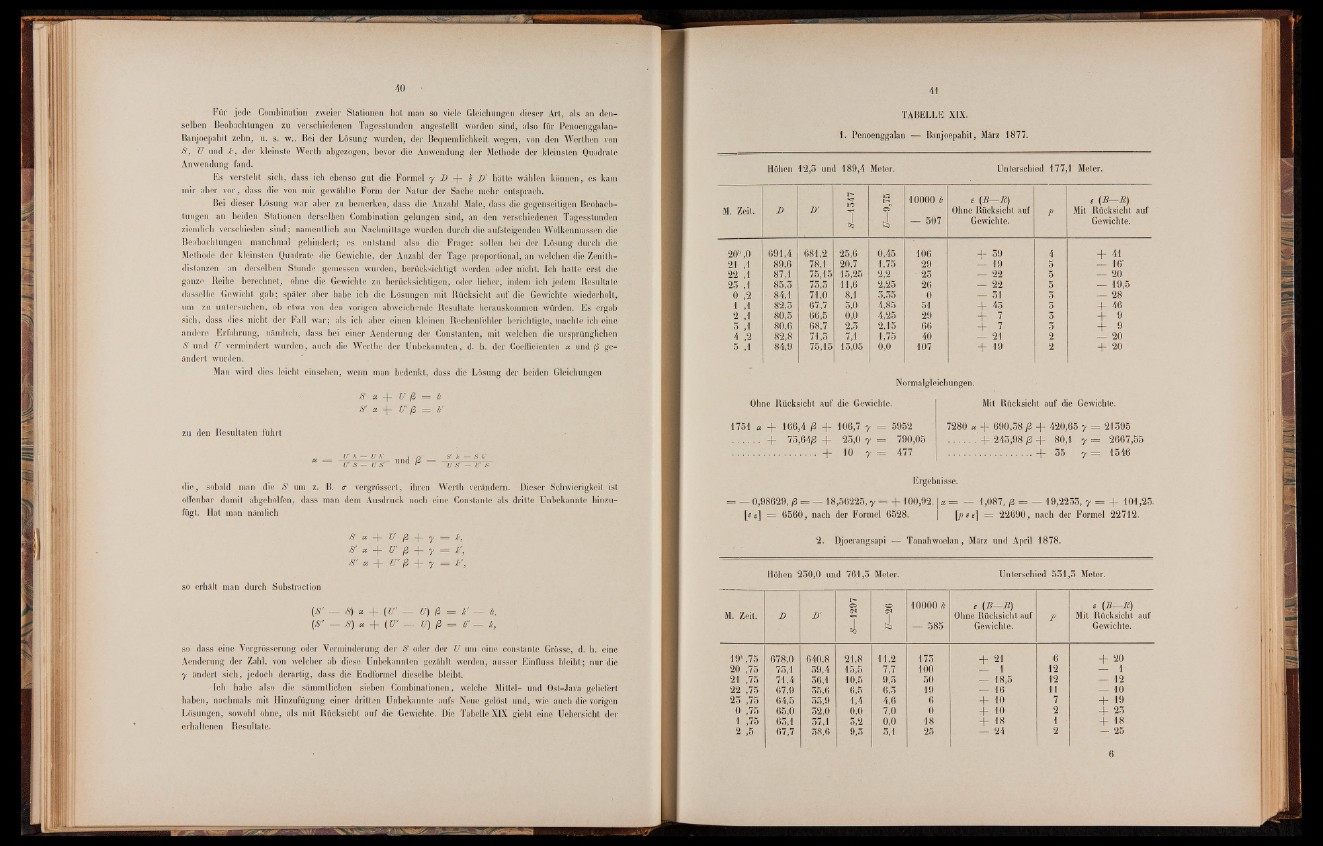
Lösungen, sowohl ohne, als mit Rücksicht auf die Gewichte. Die Tabelle XIX giebt eine Uebersicht der
erhaltenen Resultate.
TABELLE XIX.
1. Penoenggalan — Banjoepahit, März 1877.
Höhen 12,5 und 189,4 Meter. Unterschied 177,1 Meier.
M. Zeil. D D‘
irto
:
U—9,75
10000 k
i s i 5 0 7
£ (lì K)
Ohne Rücksicht auf
Gewichte.
- V
£ (B—B)
Mit Rücksicht auf
Gewichte.
20“ ,0 691,4 681,2 25,6 0,45. 106 ■ n ■ 4 1 + 41
21 ,1 89,6 78,1 20,7 1,75 29 ' — 19 5 — 16'
22 ,1 87,1 75,15 15,25 2,2 23 ^ B 2 2 5 ^ ■ 2 0
25 .1 85,5 75,5 11,6 2Ì25 26 — 22 5 ; 19,5
0 ,2 84,1 71,0 8,1 3,35 0 — 31 3 +ASÄ28
1 ,1 82,5 67,7 5,0 4,85 51 ;5 t ìf ì- 43 ' 3 + 46
2 ,1 80,5 66,5 0,0 4,25 29 ■ 9 7 3 I 9
3 ,1 80,6 68,7 2,3 2,15 66 n 7 3 H 9 4 ,2 82,8 71,5 7,1 1,75 40 — 21 2 — 20
5 ,1 84,9 75,15 15,05 0,0 107 + 19 2 + 20
Normalgleichungen.
Ohne Rücksicht auf die Gewichte. Mit Rücksicht auf die Gewichte.
1751 * 4 -166,4 ß 4 106,7 y B 5952 7280 « 4 690,38 ß 4 420,65 y = 21395
4 73,64/3 -j- 23,0 y 790,05 4 243,98/3 4 80,1- y • = 2667,55
. : . . 4 10 7 iS g j 4 7 7 y = 1546
Ergebnisse.
¿ i t - Ö , 98629, ß ’4= — 18,56225,7 = 4 100,92.1 * = — 1,087, ß ==,— 19,2253, y =±= 4 101,23.
[eg] = 6560, nach der Formel 6528. | [pee] = 22690, nach der Formel 22712.
2. Djoerangsapi — Tanahwoelan, März und April 1878.
Höhen 230,0 und 761,3 Meter. Unterschied 531,3 Meter.
M. Zeit. D D'
i-
0IM5
:
CIMD 10000 k
— 585
£ (B— B)
Ohne Rücksicht auf
Gewichte.
P
£ ( -B f e )
Mit Rücksicht auf
Gewichte.
19" ,75 678,0 640,8 21,8 11,2 173 B 2I 6 K 9 2 0
20 ,75 73,1 39,4 15,5 7,7 100 i l l B i 1 12 H B 1
21 ,75 71,4 36,1 10,5 9,3 50 — 18,5 12 — 12
22 ,75 67,9 55,6 6,5 6,3 19 — 16 11 ^ B l O
23 ,75 64,5 33,9 1,4 4,6 6 Bill 10 7 1 H
0 ,75 65,0 32,0 0,0 7,0 0 + io 2 + 23
1 ,75 63,1 37,1 3,2 0,0 18 Jim™ 1 ^ @ 1 8
2 ,5 67,7 38,6 9,3 3,1 25 2 — 25