wurde, so setzte Struve diese Unbekannte = 0 . Indem nun noch eine neue Lösung aller Unbekannten gemacht wurde,
gestaltete sich die Endformel wie folgt; (wir geben hier nur die metrische Formel);
, = (o ,o r * 8 S 3 - _ | L _ I U I — ■
w. F. ... . 5 8 5 . . . . . . . 1 495 6.58 .
wo A und JB in Metern ausgedrückt worden sind.
Diese Formel kann auch in folgender Gestalt geschrieben werden:
n / 1 79324 \ _ 20 — T (C.)
k = 0,074684 . . ( l + ’ ^ ) . 1,011888
Die Logarithmen der in dieser Formel vorkommenden Zahlen .sind:
Log. 0'074684 i | 8,87828, '
. Log.j§798ä4 == 0,25864, |
Log. 1,011888 = 0,005111.
Zum Schluss giebt Struve eine Tafel für das Produkt 0,072388 . 1,011888 und die equivalenten Produkte,
wenn der Exponent des letzten Factors in Graden Reaumur, resp. Fahrenheit ausgedrückt ist. Für die beiden anderen, von
dem Barometerstande am Beobachtnngsorte und. von der mittleren Höhe A abhängigen, sind keine Tafeln beigefügt worden.
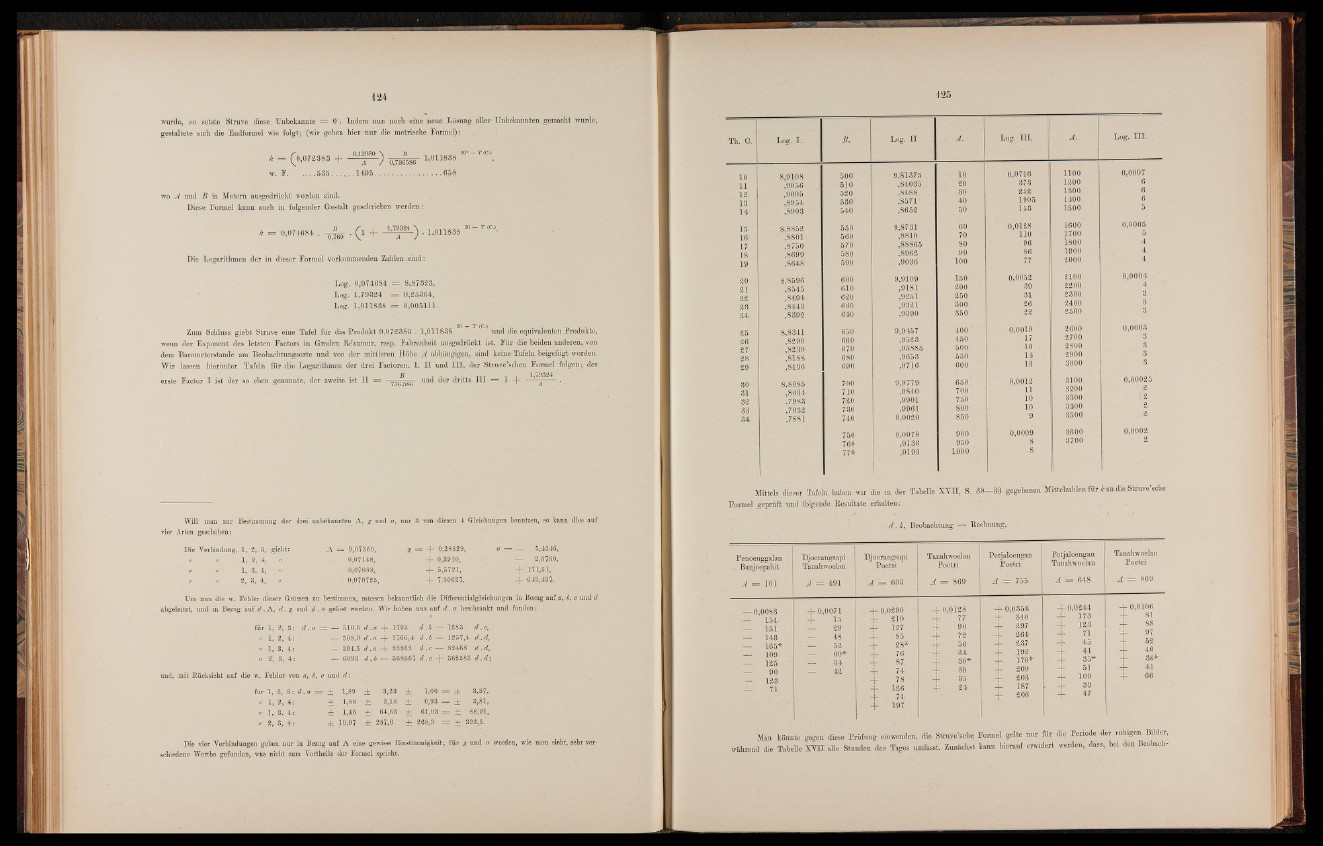
Wir lassen hierunter Tafeln für die Logarithmen der drei Factoren, I, II und HI, der Struve’schen Formel folgen; der
erste Factor I ist der • so eben genannte, der zweite ist II 73^586 .U11^ ^er H I — 1 4" •— ----- •
Will man zur Bestimmung der drei unbekannten A, % uud er, nur 3 von diesen 4 Gleichungen benutzen,
: Arten geschehen :
1 kann dies auf
Die Verbindung, 1, 2, 3, giebt:
1 I // I, 2,.4, «
// // 1, 3, 4, I
// // 2, 3, 4, //
A = 0,07360,
0,07148,
' 0,07088,
0,070725,
= -j- 0,28529,
+ • 0,3910,
+ 5,5721,
-jr 7.30627,.
er 5,4346,
- 2,5750,
4 - 171, 51, •
-f- 642,437...
Um nun die w. Fehler dieser Grössen zu bestimmen, müssen bekanntlich die Differentialgleichungen in Bezug auf a
abgeleitet, und in Bezug auf d . Ä, d . % und d . er gelöst werden. Wir haben uns auf d . er. beschränkt und fanden: -
für 1, '2, 3
» 1, 2, 4
d .a = 510,6 d . a -(- 1793 d . b — 1283' d .c,
— 508,9 d .a -(- 1766,4-' d .b — 1257,4 d .d ,
— 394,5 d .a + 82862 d . c — 82468 d .d ,
111116093 d*b;^-*ß68j3M d .c -^’^362583 d.d.-,
und, mit Rücksicht auf die w. Fehler von a, b, c und d:
für 1, 2, 3
// 1, 2, 4 ± 1,88 ± . 3,18
± 1,46 ± 64,63
± 10,97 .+ 287,6
± 1,00 = ± 3,87,
± 0,93 == ± 3,81,
± 61,03 = ± ' 88,91,
+ 268,3 = + 393,5.
Die vier Verbindungen geben nur in Bezug auf A eine gewisse Einstimmigkeit; für % und a werden, wie man sieht, sehr verschiedene
Werthe gefunden, was nicht zum Vortheile der Formel spricht.
•Th. O. Log. I. Log. n ... A . . Log. IH, A .. Log. i n .
' ' 10 ■
- 1.1
... 12
• 18' 5
14-
8,9108 '
,9056
,9005 •
,8954 '
• ;8903 • 1
500 •
•510
520 •
- -',580'
540
- 9,81375
,84035
,8488
,8571 •'
,8652
10 •
20
.3 0 ,
4 0 '
50
0,0716
373 :
252
1905
158
1100 «
1200
1300.
1400
1500 :
• 0,0007
6
. 6 .
6 1
5
15
16
17-
18
19
, 8,8852
';j8801
,8750 .
,8699
,8648
. 550
. 5 6 0
570 ,
- ■Sil.-""'"
- 590 ••
9,8731
,8810'v .'
,88.865 •
,8962
. ,9086
60
' 70 -
- 80
' 90 "
• 100
0,0128
110 •
96
' 86
77
1600
.1700 -
1800
' 19Ó0
2000
.. 0,0005
4 .
' : \4’ ■ ‘
4
20
21
22
28
24
8,8596
, ,8545
,8494
,8443
,8392
600
610
620
630
640
9,9109
,9181
,9251
,9321
- ' |y9390 -
150
200
250
-, lp o tvl-
350
0,0052
89
81
26
22
_ 2100- .
2200
2300
2400
2500
0,0004
43
33
25
26
. 27
"'■.28''
8,8841
; ,8290
-,8239
,8180
1 -;81'86
650
660
670
680
690
'9,9457
,9528
,95885
,9653
,9716
" 400 ',: ‘
450
50p;
550
600
f l f l p i l 9
17
16 c
14 >
13
2600
2700
2800
2900 ;
' 30005%
0,0003
5
. 3
■' 3
3
30
. 81
32 ‘
83
34
. 8,8085
‘ ,8034..
,7983
,7932
,7881 ...
700.
f io •
720
730:‘--A
740
9,9779
,9840 ■
,99.01
,9961 ,
0,0020
. 650
700
750
1 8 0 ° ®
.8:50 ,V
0,0012
. 11
,10
¿ '4 4 o =■
9
3100
82.00
, ■3800.
3400
‘■35.00 >
- .0,00025 BflB 1 b2 ■ 1 ‘
.2.' .
. 2
750
7 6Q H
770
0,0078 '
,0136
,0193
900
950 ’
1000
0,0009
8
. f l 1
3600
3700
0,0002
Mittels dieser Tafeln haben wir die in der Tabelle X V n , S.
Formei - geprüft upd folgende Resultate erhalten;
30—33 gegebenen Mittelzahlen für h an die Stmve’sche
d . k, Beobachtung —- Rechnung.
Penoenggalan
Banjoepahit
A '= 10T
Djoerangsapi
Tanahwoelan
A = 491
Djoerangsapi
Poetri-
‘ A '=^ 608
Tanahwoelan
Poetri
A — 869
^ Ä 0 0 8 3 ' lÄ .O /0 0 7 1 . + 0,0290. ' Ì o M 0,0128
- 154 + ' .15 ■ E | 210 + 77
151 29 f l 127 4 - : 90
— 148 • | | | | | | 48 + 85 - + 72
165* . .. _ 52 ' • 28* : + ' 56
— '..'109 60* 76 + 34
'^25 - ' ' 84 '■ • « 87 ' + ■ 30*
— 90 — 42 : l i 74 + 80
128 . n 78 H 85
71 126 m m 24
.. f l 74
• + 197
Petjaloengan
Poetri
Petjaloengan
Tanahwoelan
A = 648
Tanahwoelan
Poetri ,
-1- 0,0354
f l f l
f l
+
f l
f l
+
f l
340
297
264 '
237
.192
170*
209
203:.,
187
206
4 - 0,0244
+ 173
n 12 3
+ .71
1 9 45
B 44
H .. 85*
-¥ 51 '
B 109
m 33
f l 47
4 - 0,0106
B « 1
9
88 '
g a l i 97.
52
9 40
+ 36*
■ 41 M 66
Man könnte ge^en diese Prüfung einwenden, die Struve’sehe. Formel gelte nur für die Periode der ruhigen Büder,
während die Tabelle XVII alle Stünden des Tages umfasst. Zunächst kann hierauf erwidert werden, dass, bei den Beobach