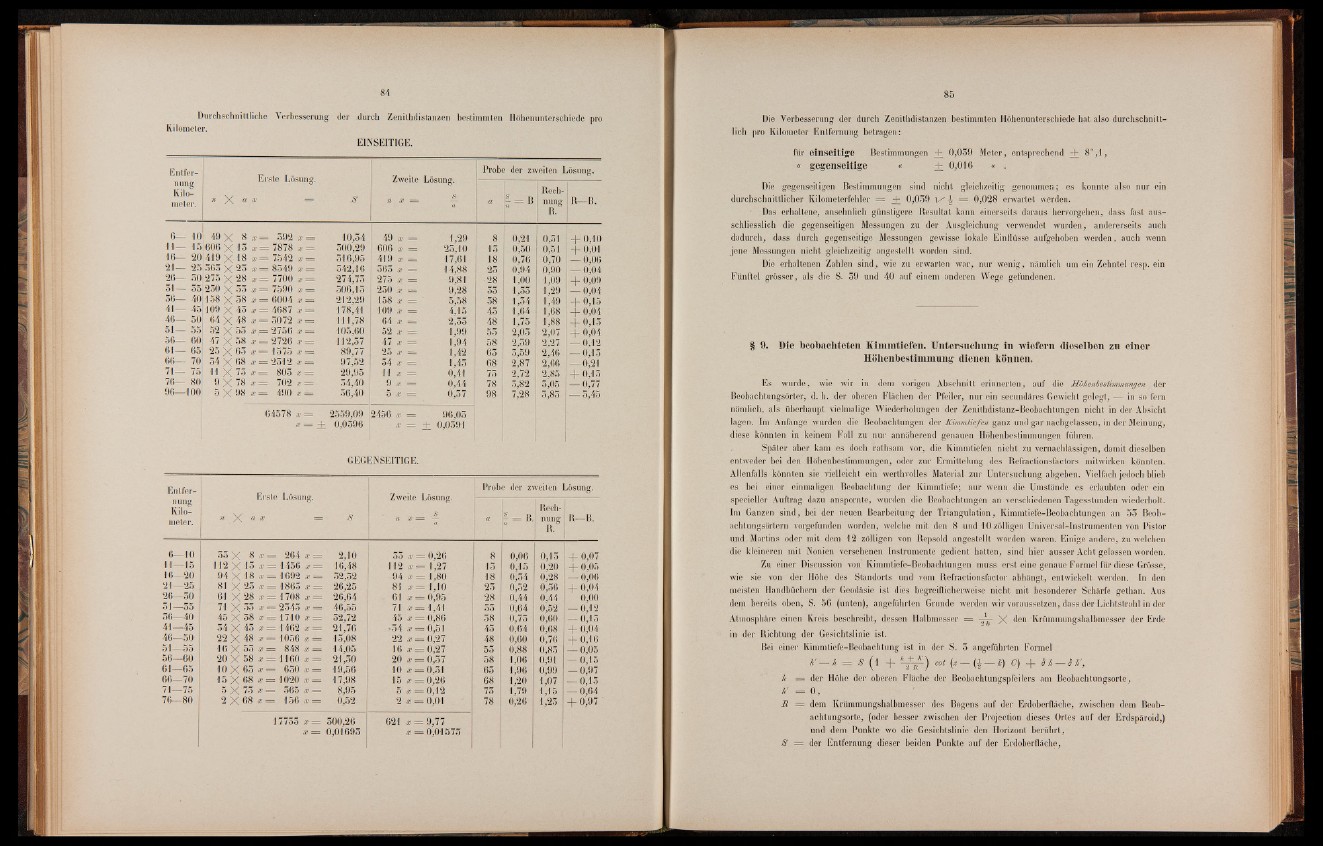
Durchschnittliche Verbesserung der durch Zenilhdistanzen bestimmten Höhenunterschiede
Kilometer.
EINSEITIGE.
Entfernung
Kilo- 11
met. er. » X «
Erste Lösung.
H 1
Zweite Lösung.
Probe der zweiten jÖSUßg.
0. I b
Rechnung
R.
R—11.
6— 101 49 X 8 f l 592 x —’X 10,54 49 *';= f 1,29 8 0,21 0,51
11— 15 6 0 6 X 1 5 x =% 7878 500,29 606 x = - 25,10 15 0,50 0,51
16— 20 4 1 9 X 1 8 7542 x -gfajj 5-16,95 419 17,61 18 0,76 0,70
21— 25 5 6 5 X 2 3 x == 8549 x = + ■ 542,16 565 .r -- 14,88 25 0,94 0,90
26— 50 2 7 5 X 2 8 f l 7700 X — 274,73 275 ar+S 9,8-1 ■28 1,00 1,09
31— 55 250 X 55 x = 7590 .r. 506,15 230 9,28 53 1,55 1,29
36— 40 1 5 8 X 5 8 x — 6004 x 212,29 158 5,58 58 1,34 1,49
41— 45 109 X 45 4687 x 178,41 109 »X fi 4,15 45 1,64 1,68
46— 50 64 X 48 ä? f l 5072 x == 111,78 64 x =+ 2,33 48 1,75 1,88
51— 55 52 X 55 x = 2 7 5 6 x — 105,60 52 .r- 1,99 55 2,03 2,07
56— 60 47 X 58 ¡r = 2 720 x 112,57 47 arfl§ 1,94 58 2,59 2 27
6 l f l 65 25 X 85 x ■= 1575 89,77 25 1,42 63 5,59 2^46
66— 70 54 X 68 ¡§ ■ 2 3 1 2 * ¿ j § ¡ 97,52 54 a?^9 1,45 68 2,87 2,66
71 ' 75 -11 X 75 x = 803 29,95 11 - 0,41 75 2,72 2,85
76— 80 9 X 78 a r '3 702 ü X - ' 54,40 9 x = 0,44 78 5*82 5,05
96— 100 5 X 98 x .— 490 56,40 . 5 x = 0,57 98 7,28 5,85 i
64578 2559,09 2456 x = 96,03
x — 4- 0,0596 x — + 0,0391
GEGENSEITIGE.
Enlfeijj
riun-i
Kilometer.
Erste Lösung.
n X ’a x - — ¡V .
Zweite Lösung.
n x = —
Probe der zweiten ,ösung.
1 f l R
Rechnung
R.
R—B.
6—10 55 X 8 ,r.—-3264 x 2,-10 55 x r= 0,26 8 0,06 0,15 + 0,07
11—15 1 1 2X 15 x - 1456 älisfl 16,48 112 x,ß= 1,27 15 0,15 0,20 + 0,05
■16—20 94 X 18 * = 1692 iäpfl 52,32 94 ar= 1,80 18 0,34 0,28 __0 06
21—25 81 X 2 3 * « 4 8 6 3 x = : 26,25 81 x - 1,10 23 0,52 0,36 + »
26—30 61 X 28 arj# 1708 ¡ S f l 26,64 61 ar— 0.95 28 0,44 0,44
51—35 71 53 -.r - - 2545 p. * 9 46,55 71 x — 1,41 53 0,64 0,52 — 0*12
56—40 45 X 38 1710 x — 32,72 45 x :^= 0,86 58 0,75 0,60 — 01 3
41—45 34 X -15 1462 x = 21,76 >54 0,51 45 0,64 0,68 + 0,04
46—50 22 X.48 x¡¿= 1056 15,08 22 ltf=:0,27 48 0,60 0,76 + 0,16
51—55 16 |Üj55 ajBW848 « s f l -14,05 16 4-^= 0,27 53 0,88 0,83 0,05
56—60 2 0 X 58 4 # 1160 k’-M 21,30 20 x%= 0,57 58 1,06 0,91 — 0,15
61B65 1ÖX-63 tM 650 «§§ 0 19,56 10 ¿1= 0,31 65 1,96 0,99 — 0 97
66—70 1 5X 68 *1=1020 17,98 15 r^^=;0,26 68 1,20 1,07 __013
71&75 5 X 75 a r fl 565 8,95 5 x — 0,12 73 1,79 ■1,15 — 0 64
76—80 2 X 08 156 x = 0 . 0,52 2 *•— 0,01 78 0,26 1,25 ^ 0*97
17753 * ^0500,26 621 x ■— 9,77
xé= 0,01693 x = 0,01575
Die Verbesserung der durch Zenithdistanzen bestimmten Höhenunterschiede hat also durchschnittlich
pro Kilometer Entfernung betragen:
für einseitige Bestimmungen + 0,039 Meter, entsprechend + 8",1,
« gegenseitige « + 0,016 « .
Die gegenseitigen Bestimmungen sind nicht gleichzeitig genommen; es konnte also nur ein
durchschnittlicher Kilometerfehler == + 0,039 i x \ — 0,028 erwartet werden.
' Das erhaltene, ansehnlich günstigere Resultat kann einerseits daraus hervorgehen, dass fast ausschliesslich
die gegenseitigen Messungen zu der Ausgleichung verwendet wurden, andererseits auch
dadurch, dass durch gegenseitige Messungen gewisse lokale Einflüsse aufgehoben werden, auch wenn
jene Messungen nicht gleichzeitig angestellt worden sind.
Die erhaltenen Zahlen sind, wie zu erwarten war, nur wenig, nämlich um ein Zehntel resp. ein
Fünftel grösser, als die S. 59 und 40 auf einem anderen Wege gefundenen.
§ 9. Die Beobachteten Kimmtiefen. Untersuchung in wiefern dieselben zu einer
Höhenbestimmung’ dienen können.
Es wurde, wie wir in dem vorigen Abschnitt erinnerten, auf die Höhenbestimmungen y der
Beobachtungsörter, d. h. der oberen Flächen der Pfeiler, nur ein secundares Gewicht gelegt, — in so fern
nämlich, als überhaupt vielmalige Wiederholungen der Zenilhdistanz-Beobachtungen nicht in der Absicht
lagen. Im Anfänge wurden die Beobachtungen der Kimmtiefen ganz und gar nachgelassen, in der Meinung,
diese könnten in keinem Fall zu nur annäherend genauen Höhenbestimmungen führen.
Später aber kam es doch rathsam vor, die Kimmtiefen nicht zu vernachlässigen, damit dieselben
entweder bei den Höhenbestimmungen, oder zur Ermittelung des Refractionsfactors milwirken könnten.
Allenfalls könnten sie vielleicht ein werthvolles Material zur Untersuchung abgeben. Vielfach jedoch blieb
es bei einer einmaligen Beobachtung der Kimmtiefe; nur wenn die Umstände es erlaubten oder ein
specieller Auftrag dazu anspornte, wurden die Beobachtungen an verschiedenen Tagesstunden wiederholt.
Im Ganzen sind, bei der neuen Bearbeitung der Triangulation, Kimmtiefe-Beobachtungen an 53 Beobachtungsörtern
vorgefunden worden, welche mit den 8 und 10 zölligen Universal-Instrumenten von Pistor
ujid. Martins oder mit dem 12 zölligen von Repsold angestellt worden waren. Einige andere, zu welchen
die kleineren mit Nonien versehenen Instrumente gedient hatten, sind hier ausser Acht gelassen worden.
Zu einer Discussion von Kimmtiefe-Beobachtungen muss erst eine genaue Formel für diese Grösse,
wie sie von der Höhe des Standorts und vom Refractionsfactor abhängt, entwickelt werden. In den
meisten Handbüchern der Geodäsie ist dies begreiflicherweise nicht mit besonderer Schärfe gethan. Aus
dem bereits oben, S. 56 (unten), angeführten Grunde werden wir voraussetzen, dass der Lichtstrahl in der
Atmosphäre einen Kreis beschreibt, dessen Halbmesser = den Krümmungshalbmesser der Erde
in der Richtung der Gesichtslinie ist.
Bei einer Kimmtiefe-Beobachtung ist in der S. 5 angeführten Formel
= ä ( i B t t — *) ° ) +
h = der Höhe der oberen Fläche der Beobachtungspfeilers am Beobachtungsorte,
H o, '
B = dem Krümmungshalbmesser des Bogens auf der Erdoberfläche, zwischen dem Beobachtungsorte,
(oder besser zwischen der Projection dieses Ortes auf der Erdspäroid,)
und dem Punkte wo die Gesichlslinie den Horizont berührt,
8 =— der Entfernung dieser beiden Punkte auf der Erdoberfläche,