In diesen beiden Tabellen sind die Bestimmungen nach denSteigenden Werthen van k geordnet!
Man sieht mit einem Augenaufschlag, dass grosse und kleine Entfernungen, grosse und kleine Höhen,
grosse und kleine Zenithdistanzen sowohl unter den ersten, als den letzten Zeilen beider Tabellen vor-
kommen.
Um diese Sache aber noch besser zu untersuchen, haben wir die ermittelten Werthe von Je
auch noch nach den Entfernungen, den Höhen und den Zenithdistanzen geordnet, und jedesmal in elf
Gruppen getheiit. Bei der Theilung nach den Entfernungen und den Zenithdistanzen sind die ersten
sieben Gruppen aus zehn, die lelzten vier Gruppen aus elf einzelnen Werthen zusammengezogen; bei
der Theilung nach den Höhen aber kam eine ungleiche Theilung, wobei die Höhen berücksichtigt wurden,
zweckmässiger vor. Die Columne Je ist bei diesen Ordnungen nicht benutzt worden.
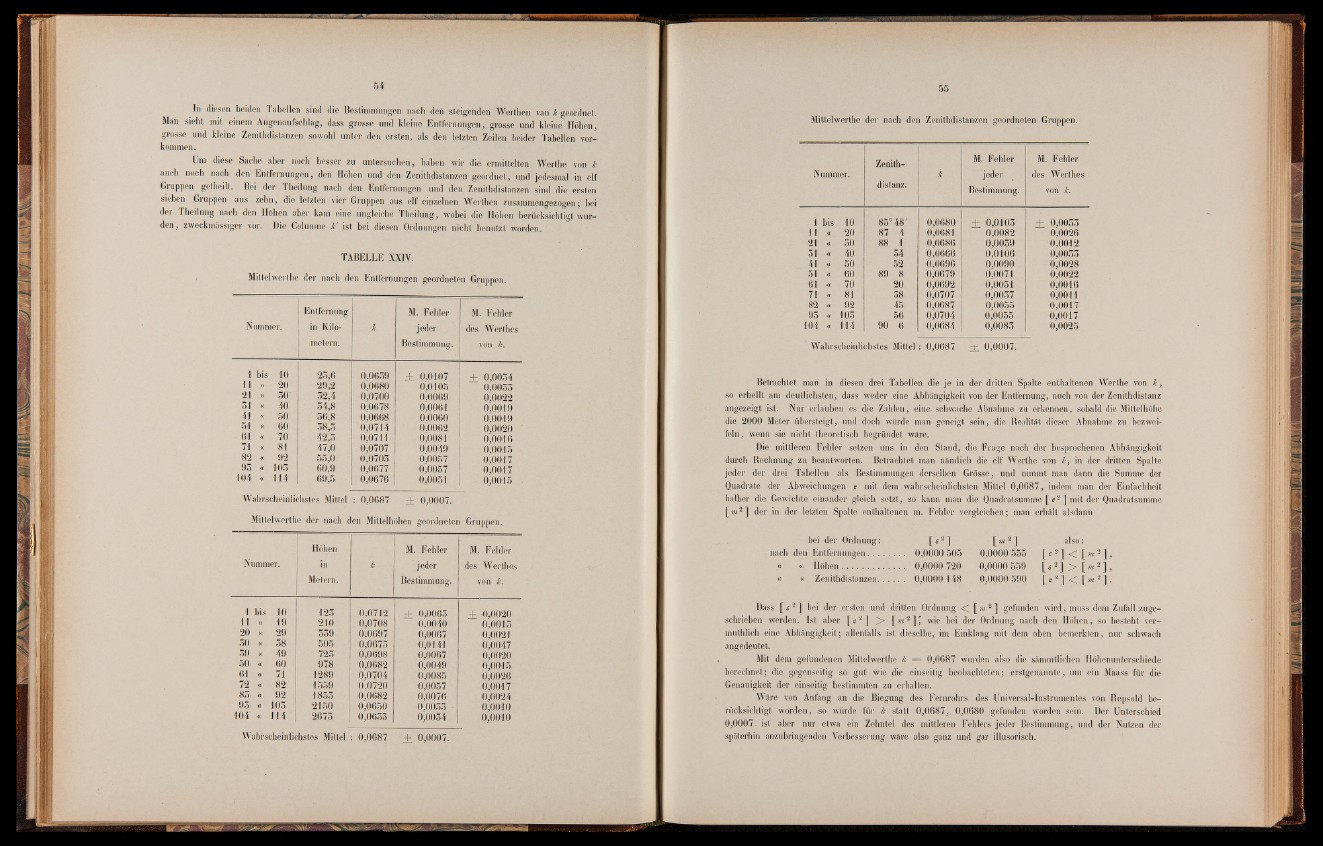
TABELLE XXIV.
Mittelwerthe der nach den Entfernungen geordneten Gruppen.
Entfernung M. Fehler M Fehler,
Nummer. in Kilo- - 4 jeder des Werth es
. metem. Bestimmung. von k.
I bis i m 23,6 0,0639 ÉÉÉ 0,0107 , d i 0,0034
11 20 29,2 0,0680 0,0105 0,0033
21 « 30 32,4 0,0700 0,0069 0,0022
31 « 40 34,8 0,0678 0,0061 0,0019
41 1 9 50 36,8 0,0668 0,0060 0,0019
51 « 60 38,3 0,0714 0,0062 0,0020
61 <( 70 42,3 0,0711 0,008! 0,0016
71 <( 81 47,0 0,0707 0,0049 0,0015
82 « 92 55,0 0,0703 0,0057 0,0017
93 <( 103 60,9 0,0677 0,0057 0,0017
104 <( 114 69,5 0,0676 0,0051 0,0015
Wahrscheinlichstes Mittel : 0,0687 + 0,0007.
Mittelwerthe der nach den Mittelhöhen geordneten Gruppen.
Höhen M Fehler M Fehler
N jmmer. in k jeder des Werthes
Meiern. Bestimmung. j/yjr;on 1c.
1 bis 10 123 0,0712 Sie 0,0063 + -0,0020
11 « 19 210 0,0708 0,0040 0,0013
20 « 29 339 0,0697 0,0067 0,0021
50 « 38 505 0,0673 0,0141 0,0047
39 « 49 723 0,0698 0,0067 0,0020
50 « 60 978 0,0682 0,0049 0,0015
61 (( 71 1289 0,0704 0,0085 0,0026
72 (( ■82 1559 0,0720 0,0057 0,0017
83 (( 92 1853 0,0682 0,0076 0,0024
95 <( 103 2150 0,0650 0,0033 • 0,0010
104 (( 114 2673 0,0633 0,0034 0,0010
Wahrscheinlichstes Mittel : 0,0687 ’+ 0,0007.
Mittelwerthe der nach den Zenithdistanzen geordneten Gruppen.
Nummer.
Zenithdistanz.
ic
M. Fehler
jeder -
Bestimmung.
M. Fehler
des Werthes
■.von 4.
1 bis 10 85° 48' 0,0680 + 0,0103 f s f 0,0033
11 f l 20 87 4 0,0681 0,0082 0,0026
21 « 30 88 1 0,0686 0,0039 0,0012
31 « 40 34 0,0666 0,0106 0,0033
41 « 50 52 0,0696 0,0090 0,0028
51. « 60 89 8 0,0679 0,0071 0,0022
61 « 70 20 0,0692 0,0051 0,0016
71 C( 81 . 38 0,0707 0,0037 0,0011
82 <1 92 45 0,0687 0,0055 0,0017
93 « 103 56 0,0704 0,0055 0,0017
104 « 114 90 6 0,0684 0,0083 0,0025
Wahrscheinlichstes Mittel: 0,0687 +] 0,0007.
Betrachtet man in diesen drei Tabellen die je in der dritten Spalte enthaltenen Werthe von Je f
so erhellt am deutlichsten, dass weder eine Abhängigkeit von der Entfernung, noch von der Zenithdistanz
angezeigt ist. Nur erlauben es dje Zahlen, eine schwache Abnahme zu erkennen, sobald die Mittelhöhe
die 2000 Meter übersteigt, und doch würde man geneigt sein, die Realität dieser Abnahme zu bezweifeln,
wenn sie nicht theoretisch begründet wäre.
Die mittleren Fehler setzen uns in den Stand, die Frage nach der besprochenen Abhängigkeit
durch Rechnung zu beantworten. Betrachtet man nämlich die elf Werthe von Je, in der dritten Spalte
jeder der drei Tabellen als Bestimmungen derselben Grösse, und nimmt man dann die Summe der
Quadrate der Abweichungen e mit dem wahrscheinlichsten Mittel 0,0687, indem man der Einfachheit
halber die Gewichte einander gleich setzt, so kann man die Quadratsumme [ e 2] mit der Quadratsumme
[ w 2] der in der letzten Spalte enthaltenen m. Fehler vergleichen; man erhält alsdann
bei der Ordnung: [ e 2 ] [ m 2 ] also:
nach den Entfernungen............... 0,0000 505 0,0000 555 [ * 2] < [ I 2 ] ,
.« « Höhen............................ 0,0000 720 0,0000 559 [ e ?t f ¡ ¡ [ * » 8] ,
. « « Zenithdistanzen 0,0000148 0,0000 590 [e2] H I B .
Dass [ e 2 ] bei der ersten und dritten Ordnung [ m 2 ] gefunden wird, muss dem ZufalL zuge-
schrieben werden. Ist aber [ e 2 ] > . [ ^ 2 ] J wie bei der Ordnung nach den Höhen, so besteht ver-
muthlich eine Abhängigkeit; allenfalls ist dieselbe, im Einklang mit dem oben bemerkten, nur schwach
angedeutet.
Mit dem gefundenen Mittelwerthe Je = 0,0687 wurden also die sämmtlichen Höhenunterschiede
berechnet; die gegenseitig so gut wie die einseitig beobachteten; « erstgenannte, um ein Maass für die
Genauigkeit der einseitig bestimmten zu erhalten.
Wäre von An fang- an die Biegung des Fernrohrs des Universal-Instrumentes von Repsold berücksichtigt
worden, so würde für Je statt 0,0687, 0,0680 gefunden worden sein. Der Unterschied
0,0007. ist aber nur etwa ein Zehntel des mittleren Fehlers jeder Bestimmung, und der Nutzen der
späterhin anzubringenden Verbesserung wäre also ganz und gar illusorisch.