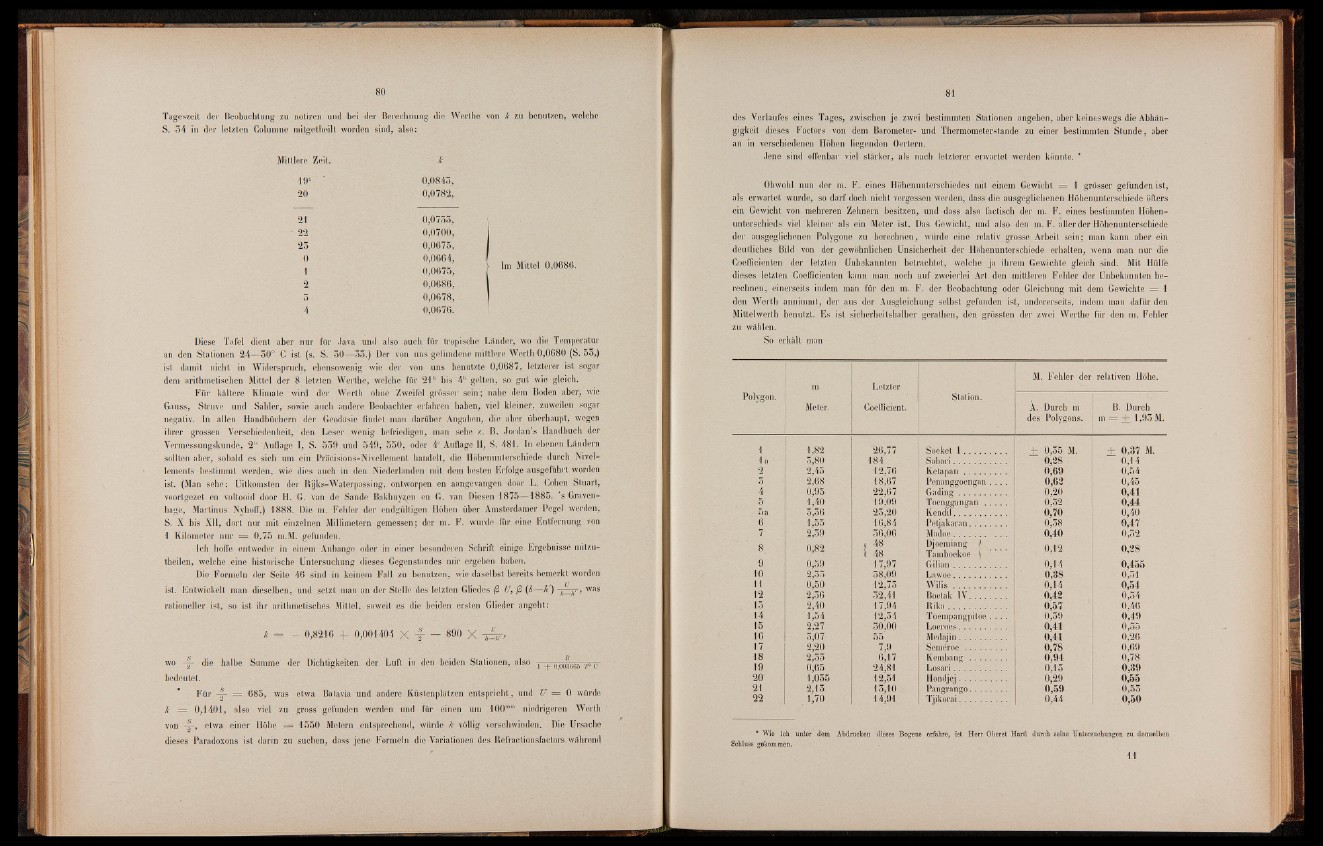
Tageszeit der Beobachtung zu notiren und bei der Berechnung die Werlhe von k zu benutzen, welche
S. 54 in der letzten Columne mitgctheilt worden sind, also:
Miltlere Zeit. k
49u , ' 0,0845,
20 0,0782,
21 0,0755,
• 22 0,0700,
25. 0,0675*
0 0,0664,
1 0,0675,
2 0,0686,
5 0,0678,
4 0,0676.
Im Mittel 0,0680.
Diese Tafel dient aber nur für Java und also auch für tropische Länder, wo die Temperatur
an den Stationen 24—50° G ist (s. S. 50—55.) Der von uns gefundene mittlere Werth 0,0680 (S. 55,)
ist damit nicht in Widerspruch, ebensowenig wie der von uns benutzte 0,0687, letzterer ist sogar
dem arithmetischen Mittel der 8 letzten Werthe, welche für 21h bis 4h gelten, so gut wie gleich.
Für kältere Klimale wird der Werth ohne Zweifel grösser sein; nahe dem Boden aber, wie
Gauss, Struve und Sabler, sowie auch andere Beobachter erfahren haben, viel kleiner, zuweilen sogar
negativ. In allen Handbüchern der Geodäsie findet mau darüber Angaben, die aber überhaupt, wegen
ihrer grossen Verschiedenheit, den Leser wenig befriedigen, man sehe z. B. Jordan’s Handbuch der
Vermessungskunde, 2te Auflage I, S. 559 und 549, 550, oder 4e Auflage II, S. 481. In ebenen Ländern
sollten aber, sobald es sich um ein Präcisions-Nivellement handelt, die Höhenunlerschiede durch Nivellements
bestimmt werden, wie dies auch in den Niederlanden mit dem besten Erfolge ausgeführt worden
ist. (Man sehe: Uitkomsten der Bijks-Waterpassing, ontworpen en aangevangen door L. Cohen Stuart,
voortgezet en voltooid door H. G. van de Sande Bakhuy^en en G. van Diesen 1875—1885. ’s Graven-
hage, Martinus Nyhoff,) 1888. Die m. Fehler der endgültigen Höhen über Amsterdamer Pegel werden,
S. X bis XII, dort nur mit einzelnen Millimetern gemessen; der m. F. wurde für eine Entfernung von
1 Kilometer nur |p= 0,75 m.M. gefunden.
Ich hoffe entweder in einem Anhänge oder in einer besonderen Schrift einige Ergebnisse mitzu-
theilen, welche eine historische Untersuchung dieses Gegenstandes mir ergeben haben.
Die Formeln der Seite 46 sind in keinem Fall zu benutzen, wie daselbst bereits bemerkt worden
ist. Entwickelt man dieselben, und setzt man an der Stelle des letzten Gliedes ß TJ, ß (7i— h') fp Ä S was
rationeller ist, so ist ihr arithmetisches Mittel, soweit es die beiden ersten Glieder angeht:
iin J B L 0,8216 H 0,001404 I - f » - 890 X
wo die halbe Summe der Dichtigkeiten der Luft in den beiden Stationen, also 1 + 0003665
bedeutet.
Für == 685, was etwa Balavia und andere Küstenplätzen entspricht, und U = 0 würde
Je ~<=®0,1401, also viel zu gross gefunden werden und für einen um 100mm niedrigeren Werth
von - |- , etwa einer Höhe == 1550 Metern entsprechend, würde k völlig verschwinden. Die Ursache
dieses Paradoxons ist darin zu suchen, dass jene Formeln die Variationen des Refraclionsfactors während
des Verlaufes eines Tages, zwischen je zwei bestimmten Stationen angeben, aber keineswegs die Abhängigkeit
dieses Factors von dem Barometer- und Thermometerstande zu einer bestimmten Stunde, aber
an in verschiedenen Höhen liegenden Oertern.
Jene sind offenbar viel stärker, als nach letzterer erwartet werden könnte. *
Obwohl nun der m. F. eines Höhenunterschiedes mit einem Gewicht == 1 grösser gefunden ist,
als erwartet wurde, so darf doch nicht vergessen werden, dass die ausgeglichenen Höhenunterschiede öfters
ein Gewicht von mehreren Zehnern besitzen, und dass also factisch der m. F. eines bestimmten Höhenunterschieds
viel kleiner als ein Meter ist. Das Gewicht, und also den m. F. aller der Höhenunterschiede
der ausgeglichenen Polygone zu berechnen, würde eine relativ grosse Arbeit sein; man kann aber ein
deutliches Bild von der gewöhnlichen Unsicherheit der Höhenunterschiede erhalten, wenn man nur die
Coefficienten der letzten Unbekannten betrachtet, welche ja ihrem Gewichte gleich sind. Mit Hülfe
dieses letzten Coefficienten kann man noch auf zweierlei Art den mittleren Fehler der Unbekannten berechnen,
einerseits indem man für den m. F. der Beobachtung oder Gleichung mit dem Gewichte = 1
den Werth annimmt, der aus der Ausgleichung selbst gefunden ist, andererseits, indem man dafür den
Mittelwerth benulzt. Es ist sicherheitshalber gerathen, den grössten der zwei Werthe für den m. Fehler
zu wählen.
So erhält man
M. Fehler der relativen Höhe.
m Letzter
Polygon. Station.
Meter. Coefficient. A. Durch m B. Durch
des Polygons. ni = S S |, 9 5 M.
1 1,82 26,77 Soeket I ................... H 0,55 M. + 0,37 M.
la 5,80 184 Sahari........................ 0,28 0,14
2 2,45 12,76 Ketapan................... 0,69 0,54
5 2,68 18,67 Penanggoengan . . . . 0,62 0,45
4 0,95 22,67 Gading...................... 0,20 0,41
5 1,40 19,09 Toenggangah . . . . . . 0,52 0,44
oa 5,56 25,20 Kendil. . . . . . . . . . . 0,70 0,40
6 1,55 16,84 Petjakaran................. 0,58 0,47
- 7 2,59 56,06 Madoe. ...................... 0,40 0,52
8 , 0,82 , 48
1 48
Djoemiang /
Taraboekoe i 0,12 0,28
9 0,59 17,97 Gilian........................ 0,14 0,455
10 2,55 58,09 Lawoe........................ 0,38 0,51
11 0,50 12,75 Wilis . . . . . . . . . 0,14 0,54
12 2,56 52,41 Boetak IV................. 0,42 0,54
15 2,40 17,94 lilka . . . . . . . . . . . 0,57 0,46
14 1,54 12,54 Toempangpitoe . . . . 0,59 0,49
15 2,27 50.00 Loeroes..................... 0,41 0,55
10 5,07 55 Medajin..................... 0,41 0,26
17. 1 2,20 7,9 Sememe'. . . . . . . . . . . 0,78 0,69
18 2,55 6,17 Kembang................. 0,94 0,78
19 0,65 24,81 Losari........................ 0,15 0,39
20' 1,055 12,51 Hondjej. . . . . . . . . . 0,29 0,55
21 2,15 15,10 Pangrango................ 0,59 0,55
22 1,70 14,91 T jikorai . . . . . . . . . . 0,44 0,50
* Wie ich unter dem Abdrucken dieses Bogens erfahre, ist Herr Oberst Hartl durch seine Untersuchungen zu demselben
Schluss gekommen.