III. Gleichzeitig, von einem
dritten Punkte aus * 0,000 450 (S* + S"*) -f- 0,000 001 (S1 — S'*)’ ’
IY. Ungleichzeitig, von einem 1
dritten Punkte aus ** I .■■-.Jfflj 0,000 450 (S* + S'1) + 0,000 001 (S‘ + S'*)
(19)
(20)
Mittels dieser Formeln wurde eine zweite Tafel der Gewichte berechnet, mit welcher aufs neue die Höhenunterschiede
ausgeglichen wurden, auf dieselbe Art, wie oben, S. 64, gezeigt wurde.
Ein dritter Versuch, aus den übrigbleibenden Unterschieden Beobachtung — Rechnung neue Werthe
der verschiedenen Categorien zu bestimmen, gab die untenstehenden Resultate:
Categorie. Bestimmungsweise. m2
I. Einseitig. 119 m% = 107,83, 0,91,
n . Gegenseitig. 54 m2 jgfjj 45,45, 0,84,
m . Gleichzeitig, von einem 1
dritten Punkte ans. 1
49 m2r= 59,47, 1 ,2 1 ,
IV. Ungleichzeitig, von einem 1
dritten Punkte aus. )
198 m2 = 262,34, 1,86,
wozu auch noch gerechnet wurde
V. Gegenseitig, von einem /
dritten Punkte aus |
54 m2 — 78,68, 1,46.
Die Zahlen müssten, im Palle dass die Gewichte ganz richtig gewesen wären, alle = 1 gewesen sein, sie sind es
aber so nahe, dass nach aller Erwartung mit ihrer Hülfe eine Gewichtstafel zu construiren war, welche allen Forderungen
entsprach. Nach einer neuen sorgfältigen DIscussion, wobei die gefundenen Fehler (B — E), nach den Entfernungen, in
Gruppen eingetheilt wurden, wurde für das dritte, endgültige System der Gewichte, die nachfolgenden Formeln entwickelt:
DEITTES SYSTEM.
Categorie. Bestimmungsweise. Gewichte.
I. Einseitig 1
p — 0,000 586 S* + 0,000 000 87 S* ’
II. Gegenseitig
III. Gleichzeitig, von einem |
1
P =
j
k j j
0,000 058 S* + 0,000 000 071 S* 5
1
dritten Punkte aus j 0,000 586 (S1 + p | + 0,000 000 87 (Sl - S 'T ’
IV. Ungleichzeitig, von einem 1 -1
dritten Punkte aus I B 0,000 586 (S1 + S” ) + 0,000 000 87 (S‘ + p f J
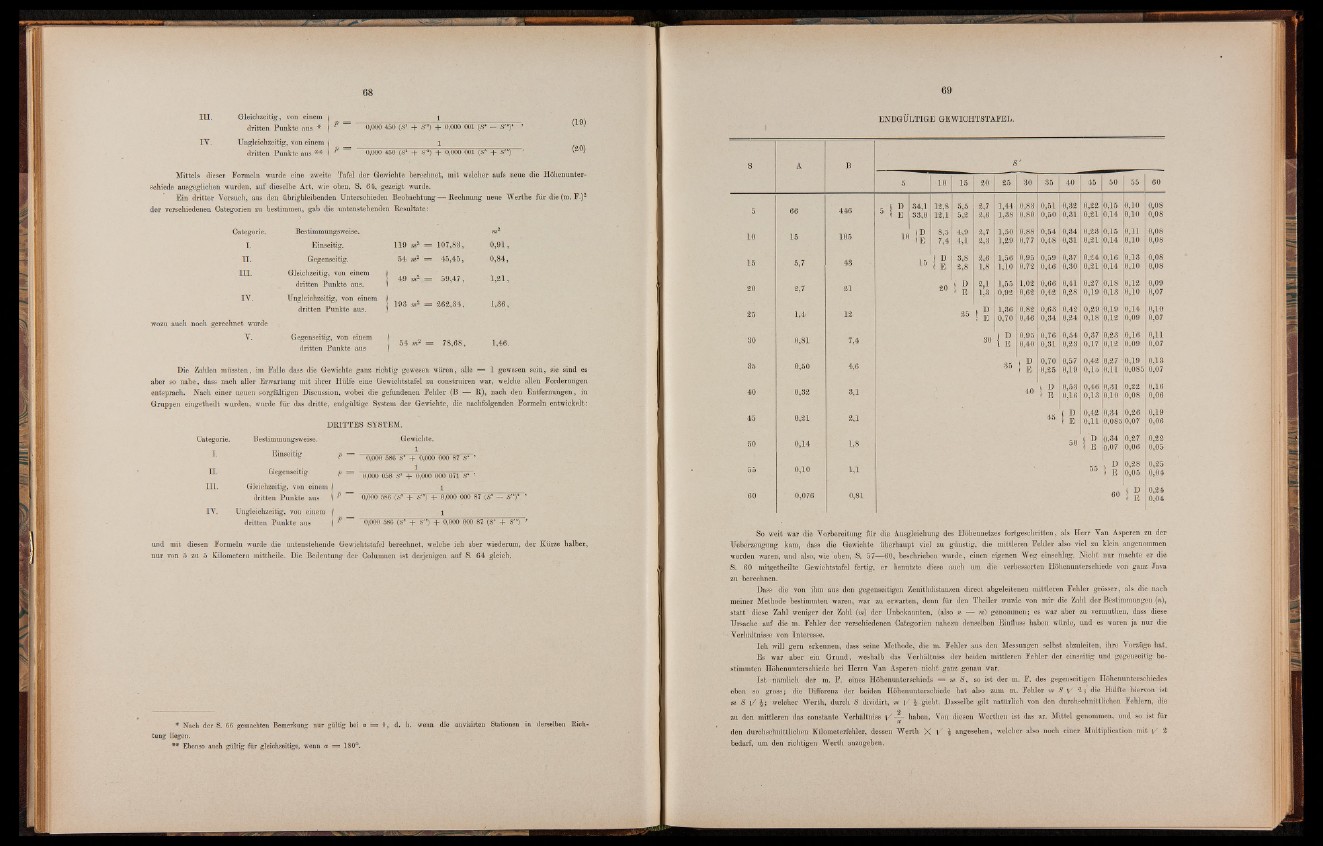
und mit diesen Formeln wurde die untenstehende Gewichtstafel berechnet, welche ich aber wiederum, der Kürze halber,
nur von 5 zu 5 Kilometern mittheile. Die Bedeutung der Columnen ist derjenigen auf S. 64 gleich.
* Nach der S. 66 gemachten Bemerkung nur gültig bei « = 0, d. h. wenn die anvisirten Stationen' in derselben Richtung
liegen.
** Ebenso auch gültig für gleichzeitige, wenn « = 180°.
ENDGÜLTIGE GEWICHTSTAFEL.
S A B S ' .
5 10 15 20 25 30 35 40 45 50 55 60
5 \ 66 446 I f £ » E
34,1
33,0
12,8
12,1
5,5
5,2
2,7
2,6
1,44
1,38
0,83
0,10'
0;51
0,50
0,82
0,31
0,22
0,21
0,15
0,14
0, 10^
0,10
0,08
0,08
.. 10 ' 15 105 10 (D
IE
8,5
7,4
4,9
4,1
2,7
2,3
1,50
1,29
0,88
0,77
0,54
0,48
0,34
0,81
0,23
0,21
0,15
0,14
0,11
0,10
0,08
0,08
15 5,7 43 15 ( D
( E
3.8
2.8
2,6
1,8
1,56
1,10
0,95
0,72
0,59
0,46
0,37
0,80
0,24
0,21
0,16
0,14
0,13
0,10.-
0,08
0,08
20 2,7 21 20 Ì D
1 E
2,1
1,3
1,55
0,92
1,02
0,62
0,66
0,42
0,41
0,28
0,27
0,19
0,18
0,13
0,12
0,10
0,09
0,07
25 1,4 12 25 !! DE
1,36
0,70
0.82
0,46
0,63
0,34
0,42
0,24
0,29
0,18
0,19
0,12
0,14
0,-09
0,10
0,07
SO 0,81 7,4 80 1 0,95
0,40
0,76
0,31
0,54
0,23
0,37
0,17
0,23
0,12
0,16
0,09
0,11
0*07
35 0,50 \ 4,6 35 i 0 1 E
0,70
0,25
0,57
0,19
0,42
0,15
0,27
0,11
0,19
0,085
0,13
0;07
40 0,32 3,1 "1-.40? I D
1 E
0,53
0,16
0,46
0,13
0,31
0,10
0,22
0,08
0,16
0,06
45 0,21 45 I E
0,42
0,11
0,34
0,085
0,26
0,07
0,19
0,06
50 ® # , 1 4 1*8 5.0 ■I
E
0,34
0,0.7
0,27
0,06
0,22
0,05
55. ; : o ,io 1 ,1 - '• ;-55 11 ED
0,28
0,05
:Ö,25
0,04
60 0*076 0,81 ;. 60 1 D
1 E
0,24
0,04
So weit war die Vorbereitung für die Ausgleichung des Höhennetzes fortgeschritten, als Herr Yan Asperen zu der
Ueberzeugung kam, dass die Gewichte überhaupt viel zu günstig, die mittleren Fehler also viel zu klein angenommen
worden waren, lind also, wie oben, S. 57—60, beschrieben wurde, einen eigenen Weg einschlüg. Nicht nur machte er die
S. 60 mitgetheilte Gewichtstafel fertig, er benutzte diese auch um die verbesserten Höhenunterschiede von ganz Java
zu berechnen.
Dass die von ihm aus den gegenseitigen Zenithdistanzen direct abgeleitenen mittleren Fehler grösser, als die nach
meiner Methode bestimmten waren, war zu erwarten, denn für den Theiler wurde von mir die Zahl der Bestimmungen (»),
statt ’ diese Zahl weniger der Zahl (m) der Unbekannten, (also n — m) genommen; es war aber zu vermuthen, dass diese
Ursache auf die m. Fehler der verschiedenen Categorien nahezu denselben Einfluss haben würde, und es waren ja nur die
Verhältnisse von Interesse.
Ich will gern erkennen, dass seine Methode, die m. Fehler aus den Messungen selbst abzuleiten, ihre Vorzüge hat.
Es war aber ein Grund, weshalb das Verliältniss der beiden mittleren Fehler der einseitig und gegenseitig bestimmten
Höhenunterschiede bei Herrn Van Asperen nicht ganz genau war.
Ist üämlich der m. F. eines Höhenunterschieds = m S , so ist der m. F. des gegenseitigen Höhenunterschiedes
eben so gross; die Differenz der beiden Höhenunterschiede hat also zum m. Fehler m S \ / 2 ; die Hälfte hiervon ist
m S V \ welcher Werth, durch S dividirt, m \ / giebt. Dasselbe gilt natürlich von den durchschnittlichen Fehlern, die
zu den mittleren das constante Verhältniss ] / haben. Von diesen Werthen ist das ar. Mittel genommen, und so ist für
den durchschnittlichen Kilometerfehler, dessen Werth X V | angesehen, welcher also noch einer Multiplication mit \ / 2
bedarf, um den richtigen Werth anzugeben.