— l O — — I I
précision en employant une méthode d’extrapolation, comme l’a Tait
M . Bl a c kma n . Les courbes de la figure VI se rattachent à une ext rapolation
pour des températures constantes et nous donnent la relation entre la
quantité de la fonction-ferment détruite et le temps de chauffage. Donc
ses courbes, d’après M. T a m m a n n seraient des courbes logarithmiques,
et en effet, elles s’en approchent assez.
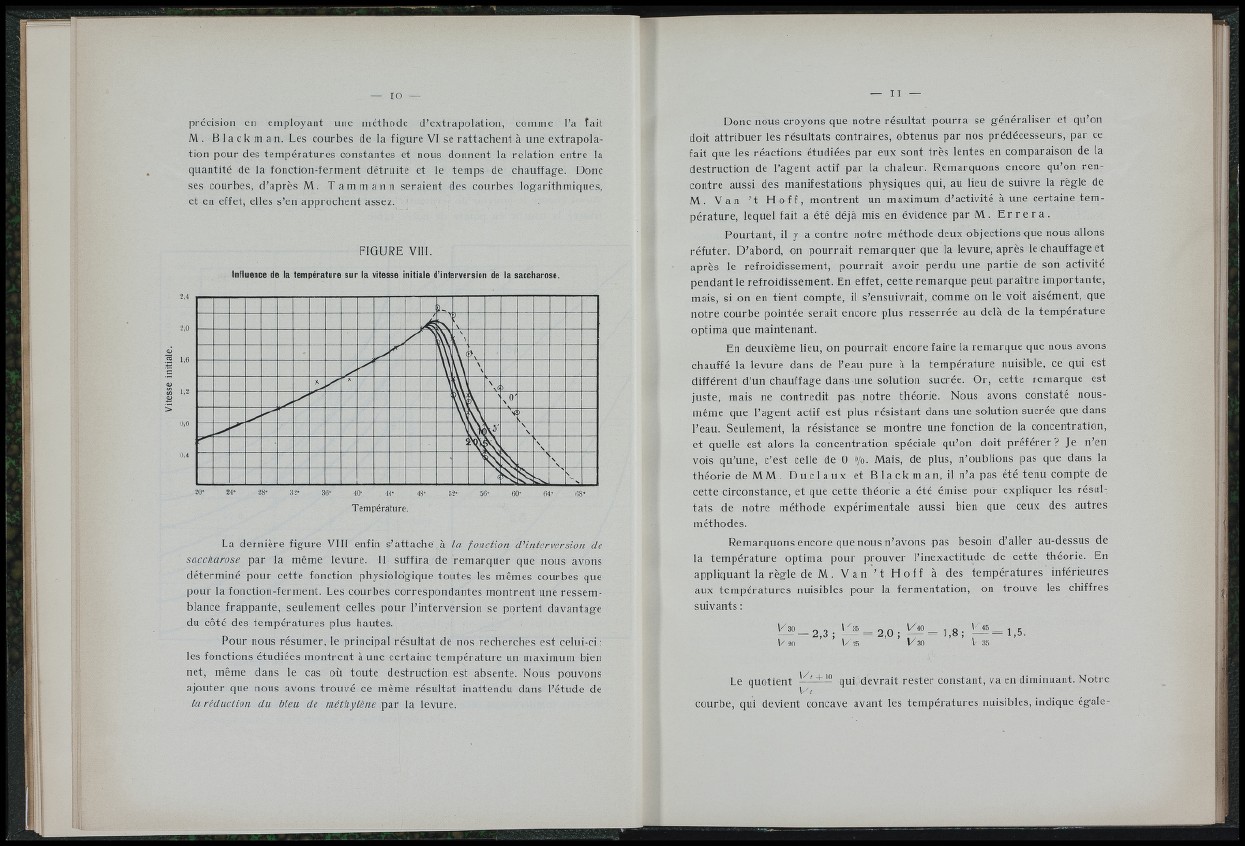
FIGURE VIII.
20" 24" 28" 3 i ” 36" 40" . 44"
Température.
52" 56" 60" 64"
La dernière figure VIII enfin s’attache à la fonction cVinterversion de
saccharose par la même levure. Il suffira de remarquer que nous avons
déterminé pour cette fonction physiologique toutes les mêmes courbes que
pour la fonction-ferment. Les courbes correspondantes montrent une res semblance
frappante, seulement celles pour l’interversion se portent davantage
du côté des températures plus hautes.
Pour nous résumer, le principal résultat de nos recherches est celui-ci :
les fonctions étudiées montrent aune certaine température un maximum bien
net, même dans le cas où toute destruction est absente. Nous pouvons
ajouter que nous avons trouvé ce même résultat inattendu dans l’étude de
la réduction du bleu de méthylène par la levure.
Donc nous croyons que notre résultat pour ra se généraliser et qu’on
doit attribuer les résultats contraires, obtenus par nos prédécesseurs, par ce
fait que les réactions étudiées par eux sont très lentes en comparaison de la
destruction de l’agent actif par la chaleur. Remarquons encore qu’on ren contre
aussi des manifestations physiques qui, au lieu de suivre la règle de
M. V a n ’ t Ho f f , montrent un maximum d’activité à une certaine température,
lequel fait a été déjà mis en évidence par M. E r r e r a .
Pour tant, il y a contre notre méthode deux objections que nous allons
réfuter. D’abord, on pourrait remarquer que la levure, après le chauffage et
après le refroidissement, pourrait avoir perdu une partie de son activité
pendant le refroidissement. En effet, cette remarque peut paraître importante ,
mais, si on en tient compte, il s’ensuivrait, comme on le voit aisément, que
notre courbe pointée serait encore plus resserrée au delà de la température
optima que maintenant.
En deuxième lieu, on pourrait encore faire la remarque que nous avons
chauffé la levure dans de l’eau pure à la température nuisible, ce qui est
différent d’un chauffage dans une solution sucrée. Or, cette remarque est
juste, mais ne contredit pas notre théorie. Nous avons constaté nous-
même que l’agent actif est plus résistant dans une solution sucrée que dans
l’eau. Seulement, la résistance se mont re une fonction de la concentration,
et quelle est alors la concentration spéciale qu’on doit préférer ? Je n’en
vois qu’une, c’est celle de 0 o/o. Mais, de plus, n’oublions pas que dans la
théorie de M M . D u c l a u x et B 1 a c k m a n, il n’a pas été tenu compte de
cette circonstance, et que cette théorie a été émise pour expliquer les résultats
de notre méthode expérimentale aussi bien que ceux des autres
méthodes.
Remarquons encore que nous n’avons pas besoin d’aller au-dessus de
la température optima pour prouver l’inexactitude de cette théorie. En
appliquant la règle d eM. Va n ’ t H o f f à des températures inférieures
aux températures nuisibles pour la fermentation, on trouve les chiffres
suivants :
- 2,3 ; _ 2,0 ; U " - 1.8 ; - 1,5.
U 20 1 / 25 \ ' 35
Le quotient -- qui devrait rester constant, va en diminuant. Notre
courbe, qui devient concave avant les températures nuisibles, indique égale