pure, mais la différence est si minime que l’erreur due à cette circonstance
peut être négligée.
En prenant toutes ces précautions, nous avons donc obtenu les quatre
courbes tracées sur la figure III. Voyons maintenant comment nous en avons
calculé la courbe pour 0 minute de chauffage, représentée par la courbe
pointée de notre planche.
*• Or, ces courbes étant connues, nous savons à quelles parties de la quantité
primitive de levure la vitesse, à une certaine température nuisible
et pour un certain temps de chauffage, est due. Mais comme la figure 1 nous
donne la relation entre la quantité de levure et la vitesse, il devient possible
de calculer la vitesse, que nous aurions trouvée dans le cas où toute la levure
aurait encore le pouvoir de fermenter. C’est de cette manière que nous avons
trouvé la courbe en pointe de notre table.
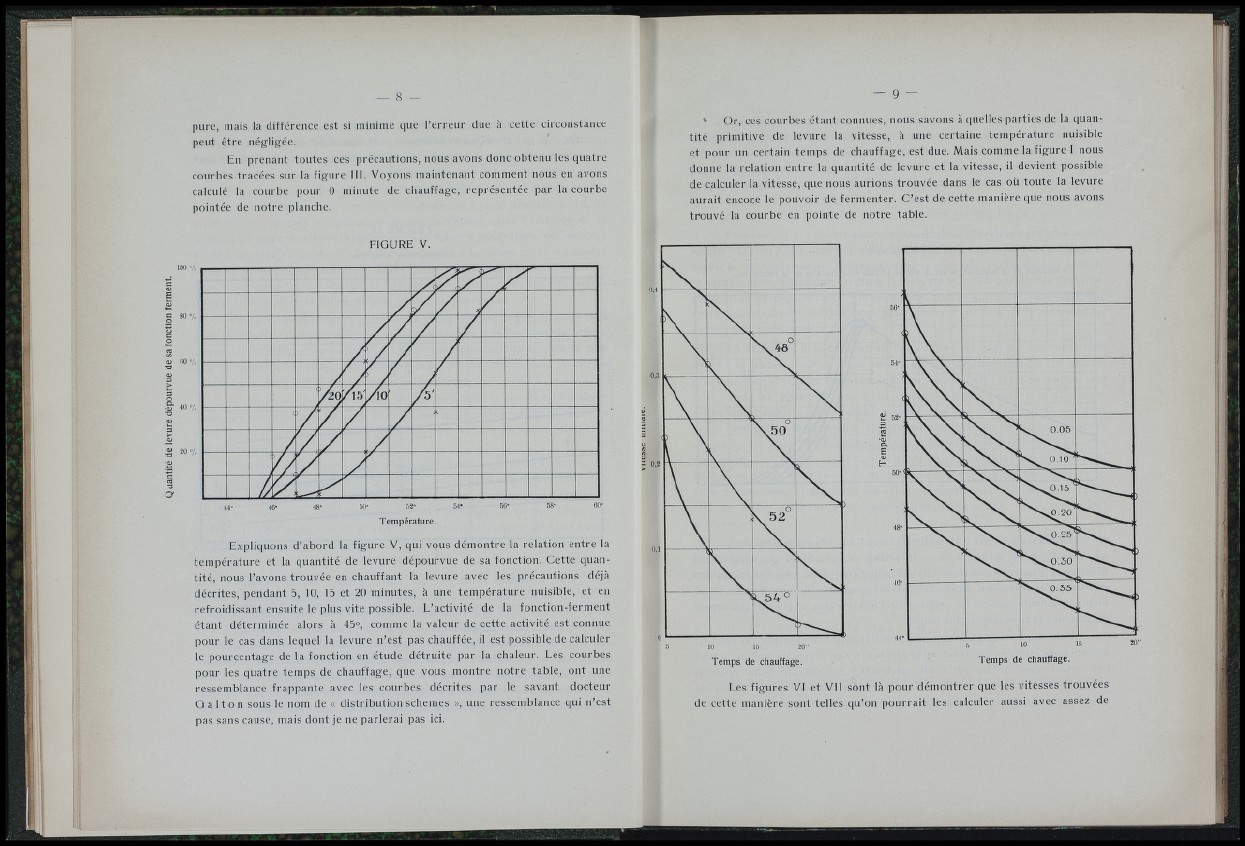
FIGURE V.
Température.
Expliquons d’abord la figure V, qui vous démontre la relation entre la
température et la quantité de levure dépourvue de sa fonction. Cette quantité,
nous l’avons trouvée en chauffant la levure avec les précautions déjà
décrites, pendant 5, 10, 15 et 20 minutes, à une température nuisible, et en
refroidissant ensuite le plus vite possible. L’activité de la fonction-ferment
étant déterminée alors à 45°, comme la valeur de cette activité est connue
pour le cas dans lequel la levure n’est pas chauffée, il est possible de calculer
le pourcentage del à fonction en étude détruite par la chaleur. Les courbes
pour les quatre temps de chauffage, que vous montre notre table, ont une
ressemblance frappante avec les courbes décrites par le savant docteur
G a i t o n sous le nom de « distribution schemes », une ressemblance qui n’est
pas sans cause, mais dont je ne parlerai pas ici.
Temps de chauffage.
Les figures VI et Vil sont là pour démontrer que les vitesses trouvées
de cette manière sont telles qu’on pourrait les calculer aussi avec assez de