k t
- - d e kans, dat de splitsing, A’allende iu de periode, na het tijdsverloop
T t reeds geschied is;
^ p = d e kans, dat de splitsing, vallende in de periode, na het tijdsverloop
T t nog niet geschied is;
en dan volgt uit de gedane waarnemingen, dat:
kf| + kt, + ktj + enz............ = kn, -1 - kn., + kn^ + enz..........
Overgaande van de reeks tijdstippen op gelijke afstanden to t h et onafge-
broken tijdverloop tusschen h et begin en h e t einde d e r p e rio d e , s te lt de lijn ,
die de p u n te n ko, k ,, k., enz. v e rb in d t, in h are verwijdering Amn T P de to ename
d e r kans van h e t gesplitst zijn v o o r, en Avordt h et re su lta a t d e r Avaar
neming u itg ed ru k t do o r de inhouden d e r s tu k k en , Avaarin genoemde lijn den
regthoek onder T P en T N v e rd e e lt, aan elkander gelijk te nemen.
Voor het begin der periode kan de splitsing, binnen haar tijdsverloop vallende,
in geen geval geschied zijn, op het einde moet zij in allen ge\’alle
zijn gebeurd. Voor het eerste oogenblik is dus k t = o en k n = T N ; voor het
laatste: k t = T N en kn — o. In het algemeen is de kans van het g e s p l i t s t
z i j n , voor elk tijdstip, gelijk aan de som der kansen van het g e s p l i t s t
AA’ o r d e n , voor al de vroegere tijdstippen zamengenornen. Van het begin naar
het einde der periode gerekend, kan dus de kans dat de splitsing reeds geschied
is nimmer kleiner AA'orden, maar moet aangroeijen met elk oogenblik
Avaarin splitsing mogelijk is. Derhalve is altijd k tu > (of hoogstens = )
Aan deze eischen Avordt v o ld a an , Avanneer u it h et p u n t T eene reg te lijn als
diagonaal getrokken Avordt, die den reg th o ek in tAvee gelijke en gelijkvormige
driehoeken verdeelt. De eischen zijn niet bepaald g en o eg , om g e e n a n d e r
verloop (van eene stijgende kromme lijn) t o e t e l a t e n , en dus kan de
diagonaal alleen Avorden aangemerkt als de eenvoudigste voox-stelling van de
to e d rag t d e r z a ak , v oor zoove rre die do o r de Avaarnemingen gegeven is.
Indien Avij nu het verloop d e r kans van gesplitst te zijn vo o r h et geheele split-
singtijdvak graphisch AA'illen v o o rstellen , en daarbij ook in aanmerking nemen
die sp litsingen, Avelke in de p e rio d e , vooi'afgaande aan de tAvee bij v o o rk eu r
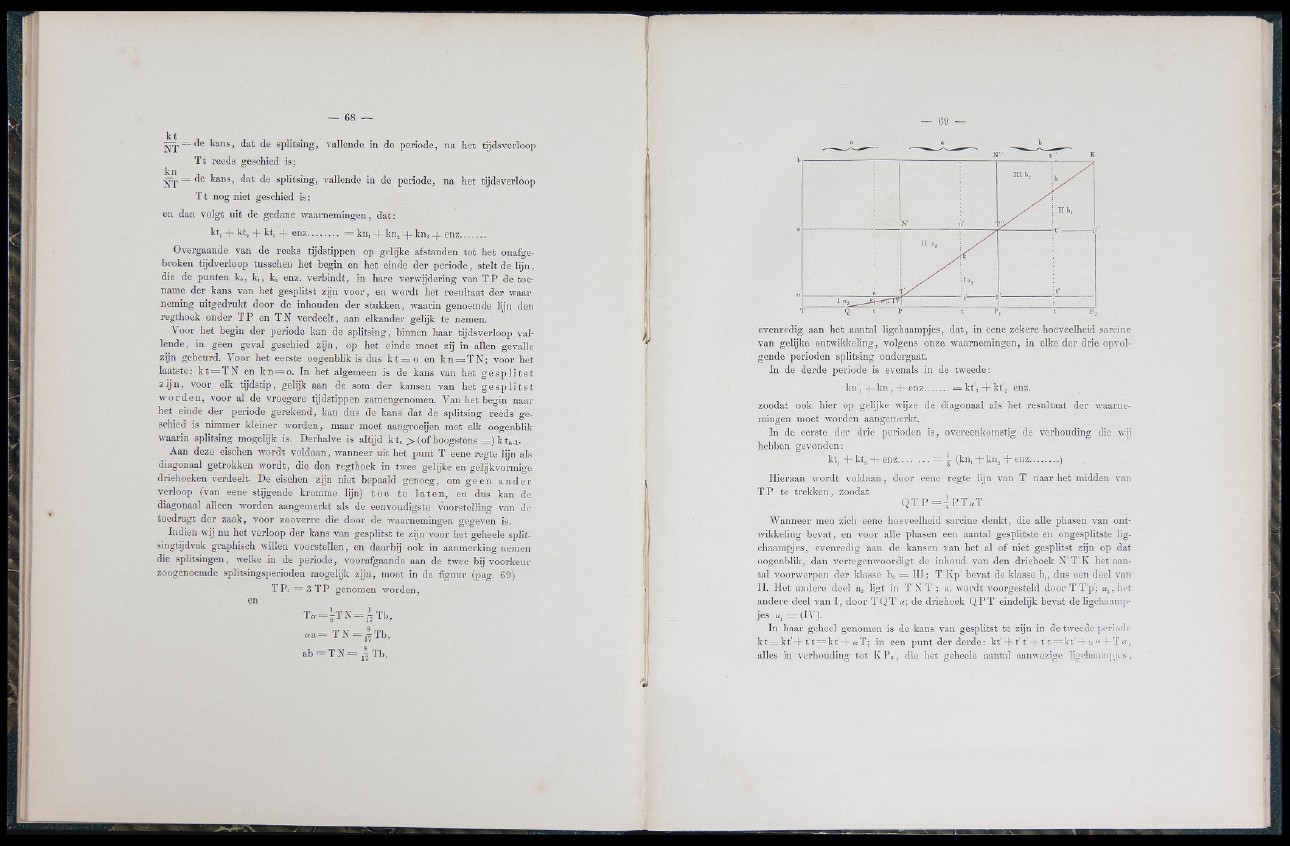
zoogenoemde splitsingsperioden mogelijk z ijn , moet in de fig u u r (pag. 69)
T I% = 3 T P genomen worden,
en
T + - ,^ T N = ^ T b ,
« a = T S = ,%rb,
ab = TN = j |T b ,
evenredig aan het aantal ligchaampjes, dat, in eene zekere hoeveelheid sarcine
van gelijke ontAvikkeling, volgens onze Avaarnemingen, in elke der drie opvolgende
perioden splitsing ondergaat.
ln de derde periode is evenals in de tweede:
k l), + k n ., + enz == k t , + kt , enz.
zoodat ook hier op gelijke wijze de diagonaal als het resultaat der Avaarnemingen
moet Avorden aangemerkt.
In de eerste der drie perioden is, overeenkomstig de verhouding die Avij
hebben gevonden:
kt, + kt, + enz.............= 3 (kn, + kn, + enz )
riie ra an AVordt v o ld a an , do o r eene reg te lijn A’an T n a a r het midden van
T P te trekken, zoodat
Q T ' j^ = 4 P T «T
AYanneer men zieh eene hoeveelheid sarcine denkt, die alle phasen van ontAvikkeling
bevat, cn voor alle phasen een aantal gesplitste en ongesplitste ligchaampjes,
evenredig aan de kansen van het al o f niet gesplitst zijn op dat
oogenblik, dan vertegenAvoordigt de inhoud van den driehoek N T K het aaii-
tal vüorAvei'pen der klasse = III: T Kp bevat de klasse b,, dus een deel A*an
II. Het andere deel a, ligt in T X’T ; a, Avordt voorgesteld d o o rT T p '; het
andere deel A’an I, door T Q T « ; de driehoek Q PT ' eindelijk bevat deligcliaamp-
jes a, = (IV).
In haar geheel genomen is de kans van gesplitst te zijn in de tAveede periode
k t^ k t ' + t ' t ^ k f - f «T; in een punt der derde: kt + 1 f + t ' t ~ k t - i - h « T « ,
alles in verhouding tot K P 2, die het geheele aantal aanwezige ligchaani]>jcs,