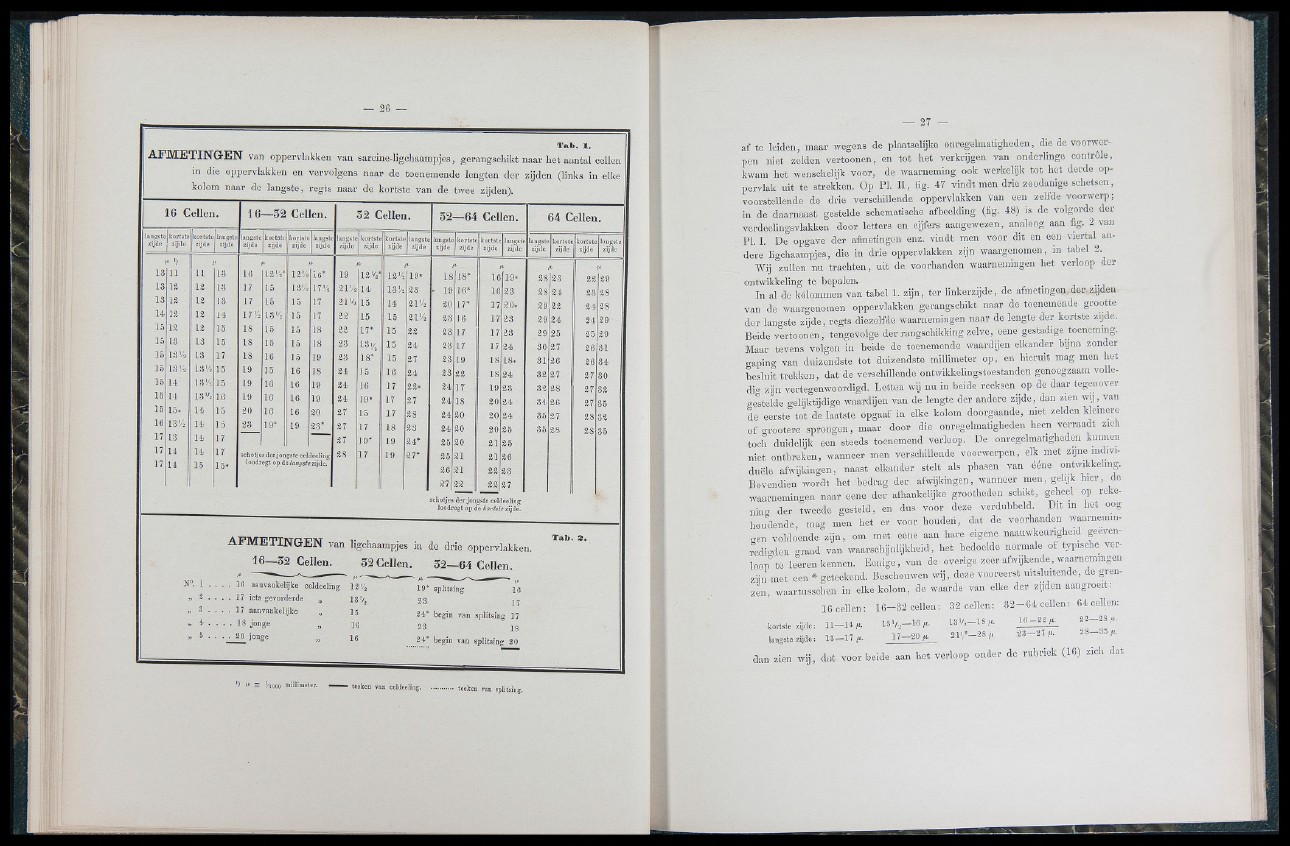
T ab . 1.
A FM E T IN G tE N van oppervlakken van sarcine-ligcliaampjes, gerangscliikt naar het aantal cellen
in die oppervlakken en vervolgens naar de toenemende le.ngten der zijden (links in elke
koloin naar de längste, regts naar de kortste van de twee zijden).
16 Cellen.
laugste kortsti
•lijde zijcle
kortste längste
zijde zijd
13
it 1)
11
!
\ 11 13
13 l ä ! 13
13 i ä 1 12 13
14 12 1 12 14
15 12 12 15
15 LS 13 15
15 13% 13 17
15 13% 13% 15
15 14 13% 15
15 14 13% 16
15 15* 14 15
16 13% 14 13
1? 13 14 17
17 14 14 17
17 14 15 15*
1 6— 52 Gelten.
längste kortste
zijde zijdi
[kortste längste
zijde zijd
10
c-
12%* 12'.> 16*
17 15 13% 17%
17 15 1 5 17
17% 13% 15 17
18 15 15 IS
IS 15 15 18
18 16 1 5 19
19 Io 16 18
19 16 16 19
19 16 16 19
20 16 16 20
23 19* 19 33*
schotjes derjongste celdeeling
loodregt op d e z i j d e . '
5 2 Cellen.
19
f*
12%* 12% 19*
2 1% 14 13% 23
21% 15 14 21%
22 15 15 21%
22 17* 15 22
23 13% 15 24
23 18* 15 27
24 15 16 24
24 16 17 22*
2 4 , [9* 17 27
27 15 17 28
27 17 18 23
27 19* 19 24*
28 17 19 27*
schotjes derjongste celdeeling
loodregt op de kortsie zijde.
A F M E T IN G E N van ligchaampjes in
16— 52 Geilen. 52 G ellen.
16 aaovankelijke celdeeling
. 17 iets gevorderde
. 17 aanvankelijke
. 18 jonge
• 20 jonge
de drie oppervlakken.
5 2— 64 Cellen.
Tab . 3 .
12%
13%
15
16
16
19* splitsing 16
23 17
24* begin van splitsing 17
23 13
24* begin van splitsing 20
af te leiden, maar wegens de plaatselijke onregelmatigheden, die de voorwerpen
niet zelden vertoonen, en tot het verkrijgen van onderlinge contrôle,
kwam het wcnschelijk voor, de waarneming ook werkelijk tot het derde oppervlak
uit te strekken. Op PI. II , fig. « vindt men drie zoodanige schetsen,
voorstellende de drie verschillende oppervlakken van een zelfde voorwerp;
in de daaniaast gestelde schematische afbeelding (fig. 48) is de volgorde der
verdeelingsvlakken door letters en cijfers aangewezen, analoog aan fig. 2 van
PI. I. De opgave der afmetingen enz. vindt men voor dit en een viertal andere
ligchaampjes, die in drie oppervlakken zijn waargenomen, in tabel 2.
Wij zullen nu trachten, uit de voorhanden waarnemingen het verloop der
ontwikkeiing te bepalen. ^
In al de kolommen van tabel 1. zijn, ter linkerzijde, de afmetingen der zijden
van de waargenomen oppervlakken gerangsohikt naar de toenemende grootte
der längste zijde, regts dlezelfde waarnemingen naar de lengte der kortste zijde.
Beide vertoonen, tengevolge der rangschlkking zelve, eene gestadige toenemmg.
Maar tevens volgen in beide dc toenemende waardijen elkander bijna zonder
»aping van duizendste tot duizendste millimeter op, en hieruit mag men liet
besluit trekkeii, dat de verschillende ontwikkelingstoestanden genoegzaam volledig
zijn vertegenwoordigd, Letten wij nu in beide reeksen op de daar tegenover
gestelde o-elijktijdige waardijen van de lengte der andere zijde, dan zien wij, van
de eerste” tot de laatste opgaaf in elke kolom doorgaande, niet zelden kleinere
of o-rootere sprongen, maar door die onregelmatigheden heen verraadt zieh
toch duidelijk een steeds toenemend verloop. De onregelmatigheden kunnen
niet ontbrelien, wanneer men verschillende voorwerpen, elk met zijne mdivi-
duële afwijkingen, naast elkander stelt als phasen van ééne ontwikkelinp
Bovendien'wordt het bedrag der afivijkingen, wanneer men, gehjk hier, de
waarnemingen naar eene der afhankelijke groothedcn schikt, geheel op reke-
niim der tweede gesteld, en dus voor deze verdubbeld. Dit m het oog
houdende, mag men het er voor houden, dat de voorhanden waarnemm-
ven voldoende zijn, om met eene aan hare eigene naauwkeurigheid peven-
redivden «raad van waarschijnlijkheid, het bedoelde normale of typische verloop”
te le”eren kennen. Eenige, van de o v e r ig e z e e r afwijkende, waarnemmgeii
zijn met ccn * geteekend. Beschouwen wij, deze vooreerst uitsluitende, de p-en-
zcn, waartusschen hi elke kolom, de waarde van elke der zijden aangroeit:
16cellen: 1 6 -3 2 o e llen : 32 cellen: 3 2 - 6 4 cellen : 64 cellen:
.„UMe u - l t , . 13V,_18,a. ¿ i z lÜ C
1 3 - 1 7 , . 1 7 - 2 ° , . 2 1 - - 2 8 2 3 - 2 7 .... 28-3=.,.,
dan zien wij, dat voor beide aan het verloop onder de rubriek (16) zieh dat
’) it = Viooo minimeter. 1 celdeeling. • teeken van splitsing.