N i l
i .
■ Al
^ En effet, on voit que cetle différence est positive,
c’est-à-dire dans le même sens, tant que n' est plus
petit que n — r.
Si l’on fail «' = « — 1, on a D = o.
Si /z' = on a D — — ^ ^ f
a 2 '
Afin de comparer plus facilement jour par jour les
états (3) et (4), cest-a-dire les étals composés avec ia
marche moyenne uniforme et ceux composés avec la
marche progessive, nous allons calculer leur différence
dans une suite de lo jour s , eu faisant « = lo, et n'
successivement = i , a , 3 lo dans l’équation gé nérale
D = i i f
2
Nous a u r o n s ’, le j o u r d u d é p a r t , D = o ;
a p r è s le i" "’ j o u r , D = - L 4 x ;
2" D = - | - 7x;
3" D = - ( - 9 x ;
4' I ) = - l - IOX = - l - z ;
5" D = - | - i o . r = - t - z ;
6» D = + 9 x ;
f D = -J- 7x ;
8" D = - 1- 4x ;
9^ D = o ;
lo " D = — 5x - f .
Une construction analogue à celle qui nous a servi
pour les marches diurnes, va rendre plus sensibles
encore les rapports que nous venons d ’étahlir.
Au moyen de la suite des états consécutifs composés
avec les marches de départ et d ’ai rivée supposées
UE L A BONITE . 381
uniformes, on conslruira deux lignes droites «lA, /«'A.
I.es ordonnées de la première seront m, ‘im . . . .nm ;
celles de la seconde seront
m + z , 2 (m + z ) ......................n [m + z).
On en construira une troisième avec les ordonnées
^ î } nÇni + 1^
c’est-à-dire avec les états calculés, en supposant que la
marche movenne a été uni forme ; et enf in, avec les
ordonnées
2 » + 1 " X 2 , 31« - F X 3 nm + X « ,
2 2j 2 2
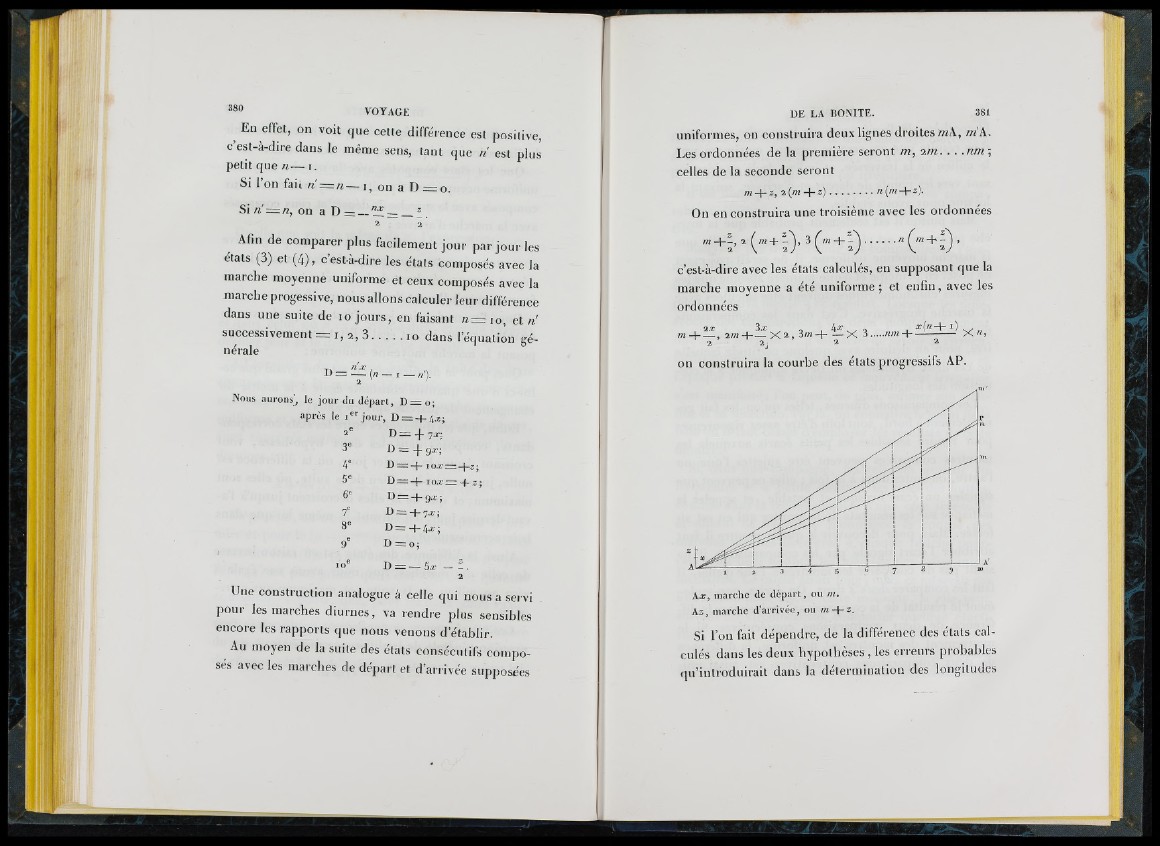
on conslruira la courhe des états progressifs AP.
A x , m a r c h e d e d é p a r t , o u ni,
K z , m a r c h e d ’a r r i v é e , o u
Si l’on fait dépendre, de la différence des étals calculés
daus les deux hypothèses , les erreurs prohahles
qu’ introduirait dans la détermination des longitudes