elle esl nul le, jusqu’aux deux termes extrêmes. L à ,
elle est maximum, et toujours égale à f . Ains i ,^es t la
2 2
limite de la différence des marches calculées dans les
deux hypothèses.
Pour faire mieux ressortir la loi suivant laquelle D
augmente depuis le milieu de la suite jusqu’aux deux
termes extrêmes, calculons dans une suile que lconque,
de 10 jo u r s , par exemple, la valeur de D pour
chaque jour. 11 suffit de faire « = i o et successivement
égal à o, I , 2, 3 ............. I O , dans l’équation
Nous aiu’ons p o u r le jo u r de départ Tl — _i.- g.f = I ^
Ap r e s le p r em i e r j o u r B = - p . / ¡ x
........................................ D = + 3 x
......................................... T> = + 2 X
/ .............................. D = + X
5' ..............................D = o
6 ' .............................. D = - X
f ..............................D = _ 2 X
8 “ .............................. D = _ 3x
9 ' ............................. D = — /Ix
............................... D = _ 5x = _ Î
2
La loi qui se produit dans cette suite d ’équations
est générale; elle résume les diverses conséquences
que nous avons déduites en discutant la valeur de D.
Du reste, on peut par un procédé géométrique rendre
ces conséquences encore plus sensibles.
Dans riiypotlièse de la marcbe progressive, la suite
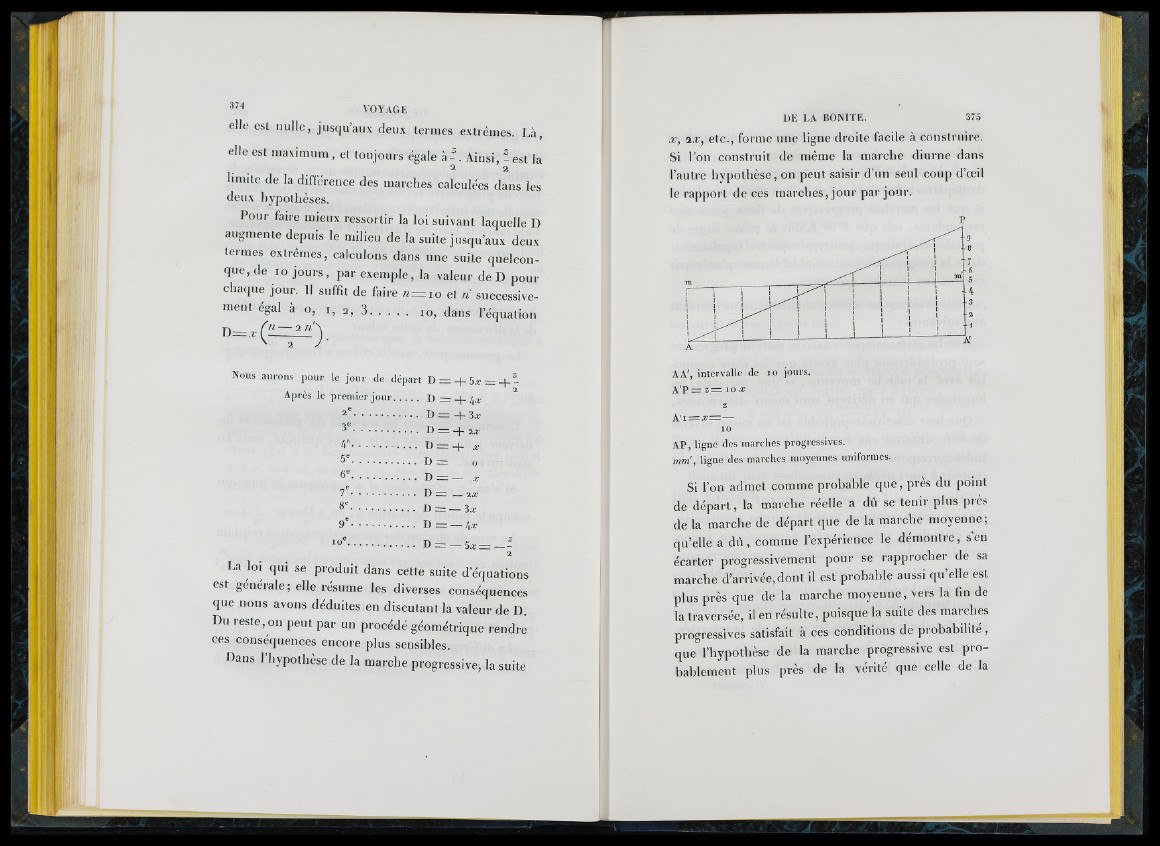
.r, a.r, etc., forme une ligne droite facile à construire.
Si l ’on construit de même la marcbe diurne dans
l’autre hypothèse, on peut saisir d’un seul coup d’oeil
le rapport de ces marches, jour par jour.
A A', in te rv a l le d e l o jo u r s .
A ' P = : z = i o x
z
+ 1—X — —
lO
A P , l igne des ma r c h e s p rogre s s ive s .
m m , l igne des ma r c h e s mo y e n n e s u n i forme s .
Si l’on admet comme probable qu e , près du point
de départ , la marcbe réelle a dû se tenir plus près
de la marche de départ que de la marcbe moyenne;
qu’elle a d û , comme l’expérience le démontre, s’en
écarter progressivement pour se rapprocher de sa
marche d’arrivée, dont il est probable aussi qu’ elle est
plus près que de la marche moyenne, vers la fin de
la traversée, il en résulte, puisque la suite des marches
progressives satisfait à ces conditions de probabilité ,
que l’hypothèse de la marche progressive est probablement
plus près de la vérité que celle de la