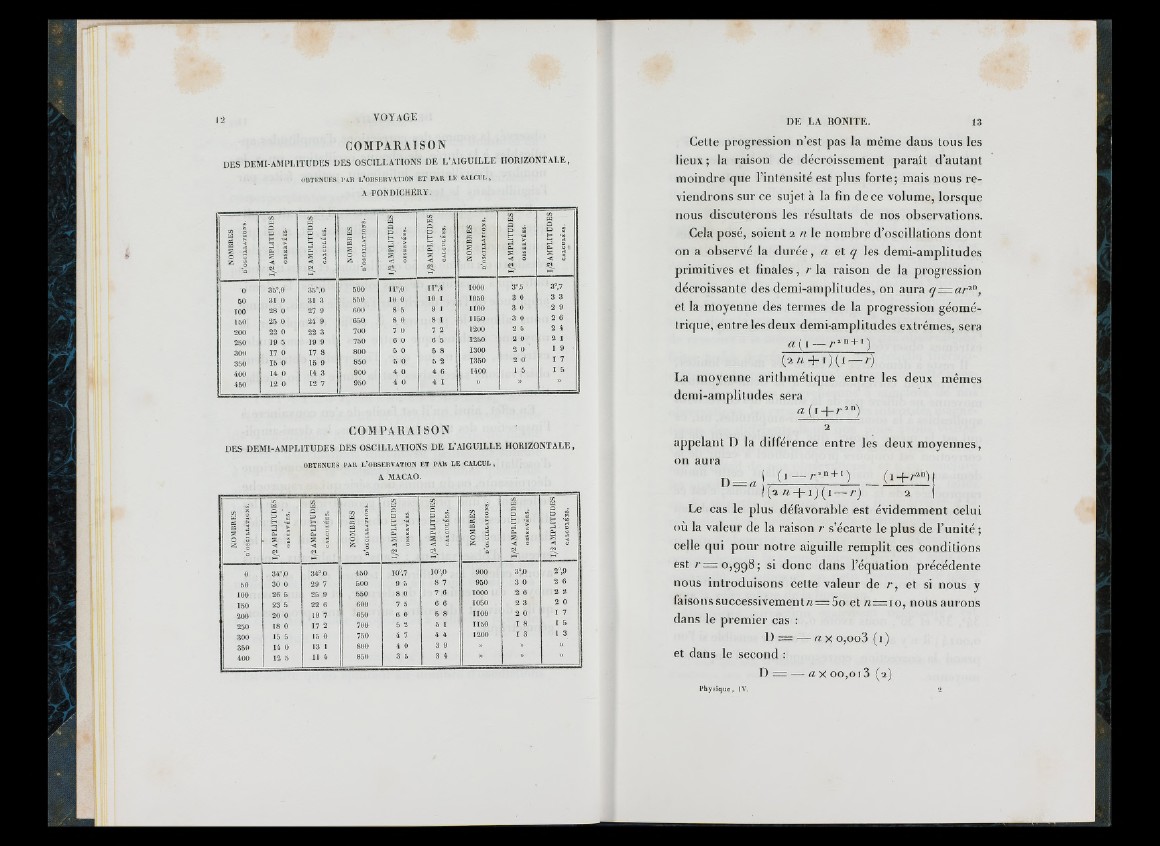
COMPARAISON
DES DEMI-AMI’L lïU D E S DES OSCILLA'ITONS DE L'AIGUILLE HORIZONTALE,
OBTENUES PAR L’üBSERVATiON ET PAU LE CALCUL,
A PONDICHÉRY.
s I
g 5
i
c u
o
‘a
y?
û 2
3 %
^ M
< ®
a •g} 2
j â
s i
-< y
S -
S i
i a
c G
» o
5
Q .
6 2
c^. %Eti
2
< o
S '
S
^ «SI
H
< s
S '
S 1
sa f-
ca 3
Ô 5
K S
u
i , É
-3 ë
C. u
■< oS
S '
S
i .S
: :3 â .
■ s i
< y
S -
0 35 ^0 35".0 500 i r , o i r ’,4 1000 3“,5 3“,7
BO 31 0 31 3 550 10 0 10 I 1050 3 0 3 3
100 28 Ü 27 9 00(1 8 5 9 I 1100 3 0 2 9
150 25 0 24 9 650 8 0 8 I I I 5 0 3 ü 2 6
200 22 0 22 3 700 7 0 7 2 12UÜ 2 5 2 4
250 19 5 19 9 750 6 Ü 6 5 1250 2 ü 2 I
300 17 0 17 S 800 5 0 5 8 1300 2 ü I 9
350 15 0 15 9 850 5 0 5 2 1350 2 0 I 7
400 14 0 14 3 900 4 0 4 6 I4Ü0 1 5 I 5
450 12 0 12 7 950 4 0 4 I ”
COMPARAISON
DES DEMI-AMPLITUDES DES OSCILLATIONS DE L ’A IGUILLE HORIZONTALE,
OBTEBUES PAR L’OBSERVATION ET PAR LE CALCUL ,
A MACAO,
» d -i o G
â
^P- 2 va
? «
’ i 1
Se
p u
cl y
■< y
(N
g 1
Cea2 ^3
O G
a 5
‘a
¡/}
aC5
U a
ta s
S
ta
c
M
1 î
12 î3
a 1
S
O .
EH3 vïSï
Sa- Su
S 2
fit
aP
S H 'U
J »
2 3
0 34",0 34°.0 450 10°,7 10°,0 900 3°.0 2°,9
50 30 0 29 7 500 9 5 8 7 950 3 0 2 6
100 2fi 5 25 9 550 8 0 7 6 1000 2 6 2 2
150 23 5 22 6 600 7 5 6 6 1050 2 3 2 0
200 20 0 19 7 650 6 0 5 8 IIOO 2 0 I 7
250 18 0 17 2 700 5 2 5 I I I 5 0 I 8 I 5
300 15 5 15 0 750 4 7 4 4 1200 I 3 1 3
350 14 ü 13 1 800 4 0 3 9 »
400 12 5 I I 4 850 3 5 3 4 ))
”
Celte progression n’est pas la même dans tous les
lieux; la raison de décroissement paraît d’autant
moindre que l’intensité est plus forte; mais nous reviendrons
sur ce sujet à la fin de ce volume, lorsque
nous discuterons les résultats de nos observations.
Cela posé, soient 2 a le nombre d’oscillations dont
on a observé la durée, a el q les demi-amplitudes
primitives et finales, r la raison de la progression
décroissante des demi-amplitudes, on aura q — ar™,
et la moyenne des termes de la progression géomé-
Iriqne, entre lesdeux demi-amplitudes extrêmes, sera
a ( 1 — » n -E I ^
(2/(-+-l)(l — /■)
La moyenne arithmétique entre les deux mêmes
demi-amplitudes sera
a ( i - l - / - ■>)
2
appelant D la différence entre les deux moyennes,
on aura
( 1 r ^ n + l ) D = a
Le cas le plus défavorable est évidemment celui
où la valeur de la raison r- s’écarte le plus de l’unité ;
celle qui pour notre aiguille remplit ces conditions
est /■= 0,998; si donc dans l’équation précédente
nous introduisons cette valeur de r , et si nous y
faisoussuccessivement« = 5o et n— io, nous aurons
dans le premier cas :
11 = — a X o,oo3 ( I )
et dans le second :
D = — a X 00,01 3 (2)
P h y s iq u e , IV. 2
i