The case is practically the same if we substitute in the place of a number of observers
working on a single object one single observer working on a number of objects which may,
or may not, be grouped in a definite series, such as a series of anthropometrical
measurements. It may be objected that anthropometrical work is done by very many
persons and therefore there is a double complexity of chances, viz. the chances of variation
in the objects observed and the chances of error in the individual observers. This
objection, however, is little more than academic. The processes of measurement are very
simple, the points to be measured are well understood, and though (as our last example
sufficiently demonstrates) there certainly will always be slight variations between the results
obtained by one anthropologist and those obtained by another on the same specimens, or
even between those obtained by the same anthropologist at different times, yet these
variations in the case of even moderately skilled workers are so infinitesimal compared
with the variations between different specimens that they may be neglected with impunity.
The most perfect land-survey ever made cannot approach in accuracy the work of the
optician, but it would be pedantry to deny its accuracy on that account.
In the measurements taken for this work it is very unlikely that even a single
observation will be so far out as to assign the object under consideration to a class
different from that in which it ought to be put
It is evident, therefore, that when a number of observers are at work making observations
upon a single object the curve in which their results may be arranged according
and^Cmves to t^le^r relative frequency is a measure of the accuracy with which the observers them-
ofFre- selves conducted their work. On the other hand, when a single observer is at work on
quency. a number of objects the curve in which the results are expressed is not a curve of the
accuracy of the observations, for we have already shown that for our purposes the lapses
from absolute accuracy may be neglected: this curve represents the degree of homogeneity
of the objects with which the observer is dealing. In the one case the agreement
of the errors of the observers with those forecast by theory, in the other the homogeneity
of the objects, is estimated by the degree in which the curve representing the actual results
approximates to the form of the perfect binomial curve. The curve which represents the
actual results may be conveniently styled a Curve of Frequency, the true ‘ binomial '
curve being usually known as the Curve of Probability. It is of the greatest importance
that the reader should clearly understand at the outset the distinction between the two.
The Curve of Frequency is a graphic representation of the actual results got by the observation
of a series of ex mples, and is obtained by grouping these results in a definite orderly
sequence from the lowest to the highest value obtained or vice versa along the scale that
is being used. The units of measurement on this scale are, at the outset, quite arbitrary,
and may represent millimetres or numbers of millimetres, grammes or numbers of
grammes, or whatever may be most suitable. The Curve of Probability is that which
would have been obtained in the same manner and on the same scale if the observations
had strictly conformed to the Law of Errors.
It has already been explained that with certain sets of observations, if the number is
sufficient to form an adequate series, the Curve of Frequency and the Curve of Probability
will coincide. In anthropometrical series, as has been shown over and over again, the same
thing will happen if, and only if, the series of examples is approximately homogeneous :
in that case the apex of the curve shows the type to which the largest number of similar
specimens conform in respect of the particular characteristic under consideration.
In other words, the apex of the curve gives the type while the sides show the
Illustration
of how the
binomial
curve
expresses
probabilities.
Relation
between
Curves of
deviation from the type, these deviations being such as the law of errors leads us to expect Relation
in a homogeneous series. By the Law of Errors such deviations should be perfectly c!SS“of
regular and equal in number alike on the sides of excess and defect. I f they are so the Probability
Curves of Probability and of Frequency will coincide exactly. Generally, however, the of p S “™
two curves deviate from one another to a greater or less degree. I f they differ <I"enc1’’
considerably in their contour then, either the number of objects under observation is
insufficient to represent adequately the true character of the series, or else the series
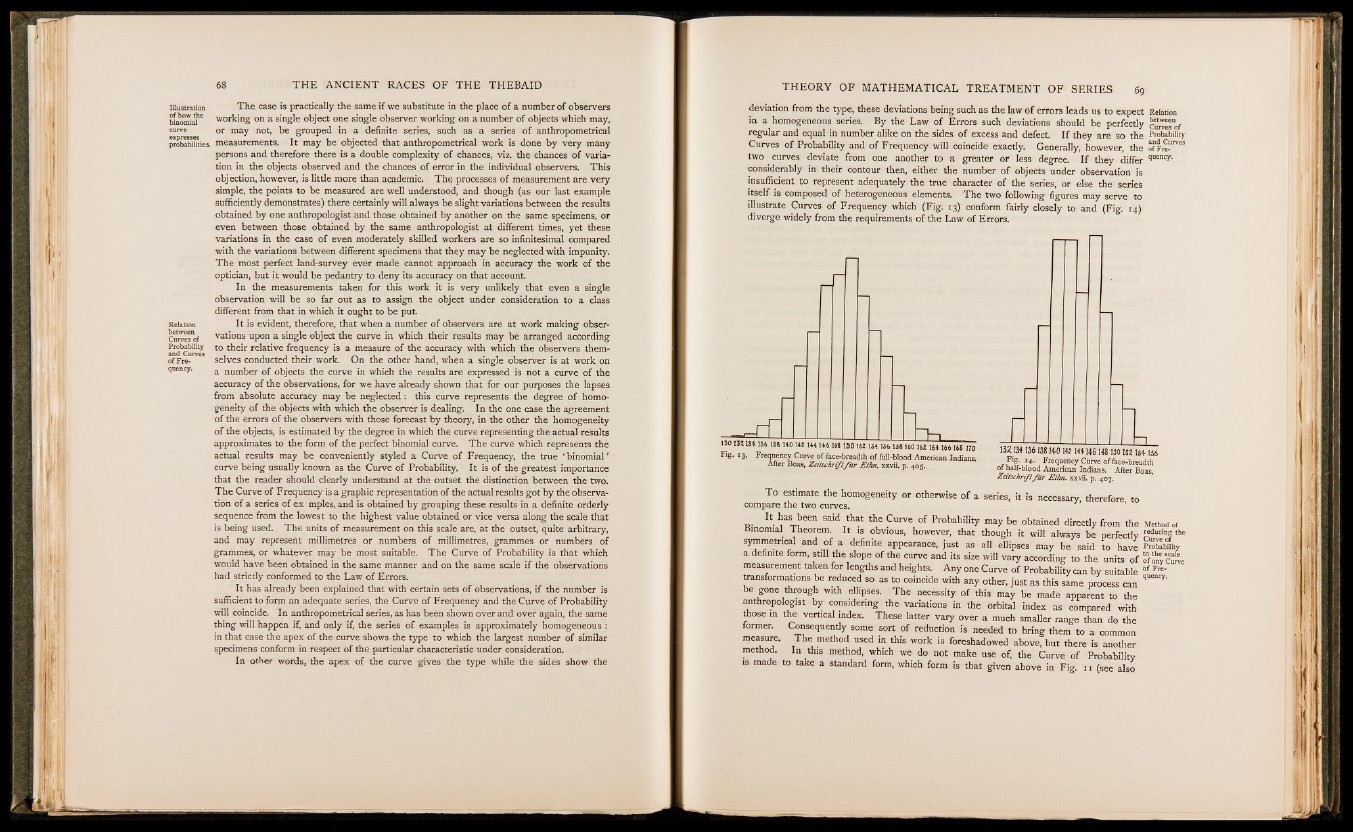
itself is composed of heterogeneous elements. The two following figures may serve to
illustrate Curves of Frequency which (Fig. 13) conform fairly closely to and (Fig. 14)
diverge widely from the requirements of the Law of Errors.
Z e its c h r iftfiir E th n . xxvii. p. 407.
To estimate the homogeneity or otherwise of a series, it is necessary therefore to
compare the two curves. ’
„ . 11 ^as„^ een said Tthat the Curve of Probability may be obtained directly from the Method of
JJmomial theorem. It is obvious, however, that though it will always be perfectly the
symmetrical and of a definite appearance, just as all ellipses may be said to have M W
a definite form, still the slope of the curve and its size will vary according to the units of
measurement taken for lengths and heights. Any one Curve of Probability can by suitable of Fre'
transformations be reduced so as to coincide with any other, just as this same process can qUen<:y'
be gone through with ellipses. The necessity of this may be made apparent to the
anthropologist by considering the variations in the orbital index as compared with
those in the vertical index. These latter vary over a much smaller range than do the
former. Consequently some sort of reduction is needed to bring them to a common
measure. The method used in this work is foreshadowed above, but there is another
method. In this method, which we do not make use of, the Curve of Probability
is made to take a standard form, which form is that given above in Fig. 11 (see also