Application
of graphic
representation.
The summit is obtained with these terms and the descent begins with the 502nd term,
of which the coefficient has the same value as that of the 499th.
To overcome the inconvenience of using lists of the numerical coefficients Quetelet’s
device of a graphic form has been very generally adopted. From what has now been said
it can readily be understood that if ‘ ordinates ’ which are proportional to the coefficients
in the binomial expansion are drawn at equal intervals from one another perpendicular
to a horizontal base, such ordinates will represent the probability that a corresponding
number of heads or tails will occur in a series of 2n trials. Quetelet illustrates the
case from betting, and asks his pupil to suppose piles of coins to be placed in a row like
the ordinates; the varying height of these piles will represent the mathematically reasonable
betting on the occurrence of the various events.
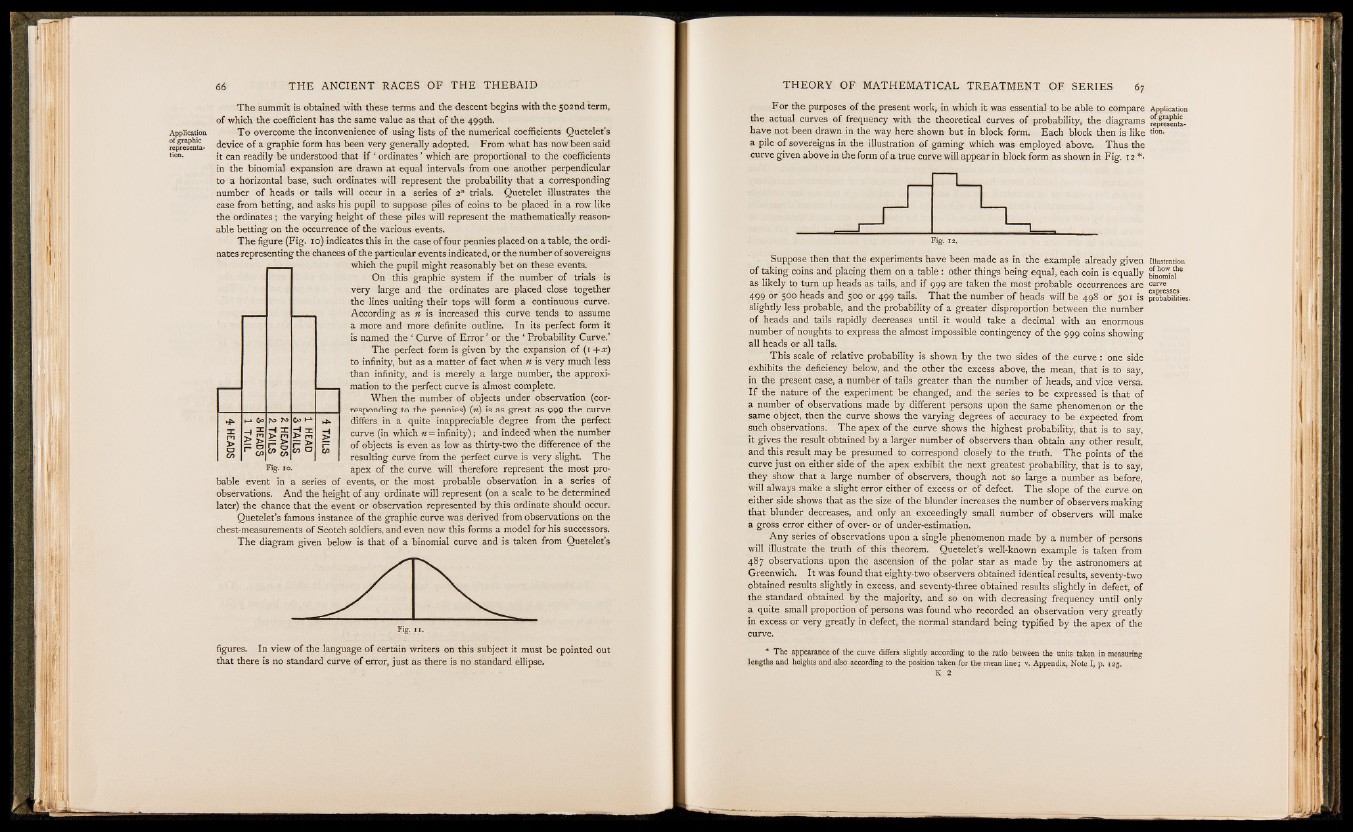
The figure (Fig. 10) indicates this in the case of four pennies placed on a table, the ordinates
representing the chances o f the particular events indicated, or the number of sovereigns
which the pupil might reasonably bet on these events.
On this graphic system if the number of trials is
very large and the ordinates are placed close together
the lines uniting their tops will form a continuous curve.
According as n is increased this curve tends to assume
a more and more definite outline. In its perfect form it
is named the ‘ Curve of Error ’ or the ‘ Probability Curve.’
The perfect form is given by the expansion of (1 + x)
to infinity, but as a matter of fact when n is very much less
than infinity, and is merely a large number, the approximation
to the perfect curve is almost complete.
When the number of objects under observation (corresponding
to the pennies) (n) is as great as 999 the curve
differs in a quite inappreciable degree from the perfect
curve (in which n = infinity); and indeed when the number
of objects is even as low as thirty-two the difference of the
resulting curve from the perfect curve is very slight. The
apex of the curve will therefore represent the most probable
event in a series of events, or the most probable observation in a series of
observations. And the height of any ordinate will represent (on a scale to be determined
later) the chance that the event or observation represented by this ordinate should occur.
Quetelet’s famous instance of the graphic curve was derived from observations on the
chest-measurements of Scotch soldiers, and even now this forms a model for his successors.
The diagram given below is that of a binomial curve and is taken from Quetelet’s
F ig . ,11.
figures. In view of the language of certain writers on this subject it must be pointed out
that there is no standard curve of error, just as there is no standard ellipse.
For the purposes of the present work, in which it was essential to be able to compare
the actual curves of frequency with the theoretical curves of probability, the diagrams
have not been drawn in the way here shown but in block form. Each block then is like
a pile of sovereigns in the illustration of gaming which was employed above. Thus the
curve given above in the form o f a true curve will appear in block form as shown in Fig. 12 *•
F ig . 12.
Suppose then that the experiments have been made as in the example already given
of taking coins and placing them on a table: other things being equal, each coin is equally
as likely to turn up heads as tails, and if 999 are taken the most probable occurrences are
499 or 50° heads and 500 or 499 tails. That the number of heads will be 498 or' 501 is
slightly less probable, and the probability of a greater disproportion between the number
of heads and tails rapidly decreases until it would take a decimal with an enormous
number of noughts to express the almost impossible contingency of the 999 coins showing
all heads or all tails.
This scale of relative probability is shown by the two sides of the curve: one side
exhibits the deficiency below, and the other the excess above, the mean, that is to say,
in the present case, a number of tails greater than the number of heads, and vice versa.
I f the nature of the experiment be changed, and the series to be expressed is that of
a number of observations made by different persons upon the same phenomenon or the
same object, then the curve shows the varying degrees of accuracy to be expected from
such observations. The apex of the curve shows the highest probability, that is to say,
it gives the result obtained by a larger number of observers than obtain any other result,
and this result may be presumed to correspond closely to the truth. The points of thé
curve just on either side of the apex exhibit the next greatest probability, that is to say,
they show that a large number of observers, though not so large a number as before,
will always make a slight error either of excess or of defect. The slope of the curve on
either side shows that as the size of the blunder increases the number of observers making
that blunder decreases, and only an exceedingly small number of observers will make
a gross error either of over- or of under-estimation.
Any series of observations upon a single phenomenon made by a number of persons
will illustrate the truth of this theorem. Quetelet’s well-known example is taken from
487 observations upon the ascension of the polar star as made by the astronomers at
Greenwich. It was found that eighty-two observers obtained identical results, seventy-two
obtained results slightly in excess, and seventy-three obtained results slightly in defect, of
the standard obtained by the majority, and so on with decreasing frequency until only
a quite small proportion of persons was found who recorded an observation very greatly
in excess or very greatly in defect, the normal standard being typified by the apex of the
curve.
* T h e appearance o f the curve differs slightly according to the ratio between the units taken in measuring
lengths and heights and also according to the position taken for the mean lin e; v. Appendix, Note I , p. 12 5.
K 2
Application
o f graphic
representation.
Illustration
of how the
binomial
curve
expresses
probabilities.