4 4 C a p . I X . S g o n b e n t g n o o ^ T a b . I V .
3(() ialtt nt(f)t »01' nótWs tiiefc Xabellc ju oer tónsent , öag Set Diameter ii6er 20
SoU entließe, roeil man (e^t feiten ï u n ï c^ ^o l g oon Wefev Si c t e gcbratirtjet.
84.
Dlac6t)«m ma n bie Ci rcumfereng juni e r cmp e l 39 30a unt> Sic Ciinge 58alcfené
a 19 3 u g «bgcnonimcn, fo mug mmi in bec t abcKc unter bcm SBoi't Ci rcumfereng 39
fucf)cn, rocldjc j um Diametro bc« s pMt ó 12 Soll 4f ? Cini cn, unb ju bcc Ciccutgiiicfte
121 geben, bicfc mu § man mi t 19, al^ ber Cange beS «Pfa^tó mul t ipl ici tcn, «nb ba^ Prod
u a mi t 144 dividi tcn ber Quotus a 15HS giebt ben 3iiftalt an Cubi cSüf f cn tinb Qibic-
3oKcn, rocictie fs f i emi t 3 dividi tet roerben, bie SopI ber Soliven a 5'r}l geben, e b en fc
operiïet man in benen übrigen gän?n.
2 7 5 8 8 19
12 •
1 7 2 8 = 1 4 4
12
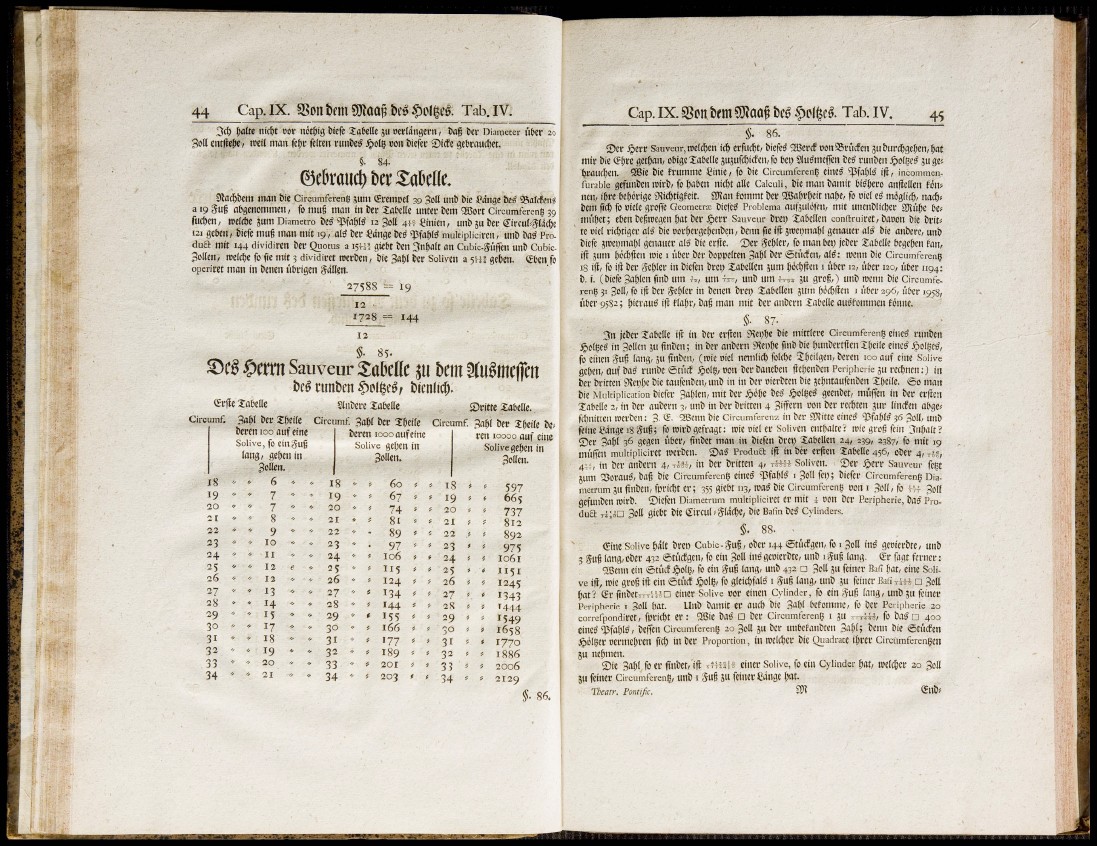
ê mn Sauveur § mtüt . 8 5 .
^ c J U D e i i t ? f u ê t n e | f e n
ï t e é c u n b m i ) i e n ( i ^ .
e r | î e XobeHe
Circumf. 3a(il bcr î j e i f e
berm 100 auf eine
Solive, fo c i n S u i
lang, gef ienin
Sollen.
Sliibete Tabelle ©r i t te Babette.
Circumf. 3aW bcr XÇeitc Ci r cumf . 3a^i bet î^e i f e 6i!<
beten 1000 auf eine ren 10000 ouf eine
Solive geOen in Solive ge^en in
Sollen.
18 - 6 - 18
1 9 7 - 1 9
20 7 - - 20
21 8 - - 21
22 9 'f 22
23 10 - 23
24 I I - 24
25 12 e - 25
26 -- 13 -, 26
3 7 13 'r 27
28 " • 1 4 " 28
29 15 29
30 - - 1 7 30
31 - 18 31
32 - 1 9 - 32
3 3 " 20 3 3
3 4 21 - 3 4
6 0
6 7
7 4
81
89
9 7
1 0 6
1 1 5
1 2 4
1 3 4
1 4 4
1 5 5
1 6 6
' 7 7
189
2 o r
203
i S
1 9
2 0
2 1
22
2 3
2 4
2 5
2 6
2 7
2 8
2 9
3 0
3 1
3 2
3 3
3 4
Sotten.
5 9 7
665
7 3 7
8 1 2
8 9 2
9 7 5
1 0 6 1
1 1 5 1
1 2 4 5
1 3 4 3
1 4 4 4
1 5 4 9
1 6 5 8
1 7 7 0
1 8 8 6
2006
2 1 2 9
C a p . I X . a s e i t b em i t è T a b . I V . ^
§. 86.
S c r § c r r Sauveur, roeleren icf) erfutfet, biefc^ 3Bercf Don58n'i(fen 5uburcSgc5en,&at
mir bie Spr e gct^an, obige Xabtlle jujufc6i(fen,fo bei; a u t o f f e n be« ruiiben j u g e ;
6rau(l;en. 9ßic bie f r umme i j inie, fo bie Ci rcumfereng eine« «Pfaf;K i(}, incommen.
furable gcfuiiben iBitb, fo Siaben nic^talle Calcul i , b i ema n b ami t bi0öero anffelien fön;
nen, i^re benötige 9?i(®tigfcit. SD!an fommt bcr ®aH'^e i t na^e, fo »icl eS möglich, nac6«
bem M fo »iele groffc Geometras bicfe« Problema aufjulófen, mi t unenblicf)er SMü^c be>
müfxt; eben beimcgen ber § e r r Sauveur brei; Xabcllcn conf t rui ret ,baoon bic bcit«
' tc »ic( ridjtiger otö bic «or^ergeitenben, benn fie ifl swctimcil)! genauer al« bie anbere, unb
bicfe jn)ei;maf;l genauer ató bic erfle. 3 e r SeWer, fo manbep jcbcr XabcUc begeben fan,
ifl 5um I)ócl)flcn roie i über bcr boppcitcn S aU bcr ©tüi f cn, alS; rocmi bic Ci r cumfereng
18 ifl, fo i|i bcr ScMcr in biefcn brci) Xabcllen äum Oócfeflcn i über 12, über 120, über 1194:
b. i. (bicfe Bafilen frnb um h , um i r s , unb um t r w 5U gco§, ) unb rocnn bic Ci rcumfereng
31 Soll, fo ifl bcr gcfjlcr in benen brei; Xabcllcn juni (jöcJdcn i über 290, über 1958,
Aber 9582; Jictau« i|t f laj i r, bag man mi t bcr anbcrn Xabclle aus fommen fönne.
§ . 87-
3 n jcbcr XabcUe in bcr crffen 9?ci;f)e bie mittlere Ci rcumfereng eine« runben
^ot|e8 in Sollen }u finbcn; in ber anbcrn 9?ei)f;c finb bie (tunbertflen tt;eile einc^ .^olgc^,
fo ciiien Sug lang, äu finbcn, (roie »iel ncmlict) folc^c ÏJe i lgen, beren 100 auf eine Sol ive
gelten, auf i a ß runbc ©tüc ! § o l g , »on bcr baneben fleitcnbcn Periphei ie ju rechnen;) in
ber britten 9?ci;{ie bie taufenbcn,unb in in ber »ierbten bie jcjmtaufenbcn X^cile, ©0 ma n
bie Miiltiplication bicfcr 3al;lcn, mi t bcr ^èt)e bcÄ ipolge« gccnbct, müffen in ber crften
XabcHe 2, in bcr aubcrn 3, unb in bcr britten 4 Si f fern uon bcr reiften j u r lincfcn abgc;
ftl)iuttcn werben: 3. <S. 5ßenn bic Ci r cumf e r enz in bcr SKitte eine« «pfa^fó 36 SoU, unb
feine e änge 18 S u § ; fo roirb gef ragt : roie oicl et Solivcn enthalte? roie grog fein 3-npa(t?
©er 3a(;[ 36 gegen über, fïnbct man in biefcn btc^ XabcUen 24, 239, 2387, fo mi t 19
müficn multipliciret rocrben. S a S P r o d u a ifl in ber crflen Xabclle 456, ober 4,
4 i i , in bcr anbcrn 4, T i n , in bcr britten 4' t » » Solivcn. ©e r § c r t Sauveur fegt
j um SBoraué, bag bic Ci rcumfereng ciuCfS »TJfoW« I Soll fei;; bicfcr Ci rcumfereng Diametrum
5U finbcn, fpridjt e t ; 355 113, roaS bie Ci rcumfereng Don 1 Sol l , fo H4 Soll
gefunben wirb. Si e f en Diametrum multipliciret er mi t i rotl ber Peripherie, bas Prod
u a r i U D Soll giebt bie ei rcu| j5tó( ( )e, bic Bafin bes Cyl inders.
§ . 88. .
(Eine Sol ivef täl t bren C u b i c - S u § , ober 144 ©tücEgen,fo i Soll in« gcoicrbtc, unb
3 Su§ lang, ober 432 ©tücfgen, fo ein Soll ins gcnicrbtc, unb 1 5ug lang, er fagt f e rne r :
aScnn ein ©tücf ipolg, fo ein Sug lang, unb 432 • Soll ju feiner Bafi fjat, eine Soli,
ve ift, roie grog ift ein ©tücf § o l g , fo gleicf)faK i Stig lang, unb äu feiner Bali t I H • Soll
{)at? & f inbet jTTiHD einer Sol ive sor einen Cy l inde r , fo ein Sug lang, unb ju feiner
Peripherie i Soll f)at. Unb bamit er aut() bic Sal;l bcfommc, fo ber Peripherie 20
correfpondirct, fpr i t j t e r : 5Bie ba« • ber Ci rcumfereng I 5U ^nUi, fo ba« • 400
cine«^fal)l«, beffen Ci rcumfereng 20 Soll JU bcr unbcfanbtcn 3a!;t; beim bie ©tücfcn
,^Ó!ger »ermcprcn fid) in bcr Proport ion, in roeleder bic Quadrate il;tcr Ci rcumfercngcn
JU ncl;mcn.
S i c 3a(>l fo er fïnbct, ifl einer Solive, fo ein Cyl inder fiat, roelciier 20 3oa
5U feiner Circumfereng, unb i 3ug 5" feiner edngc !)at.
Theatr. Fontific. ffnb»