42 Cap. I X . §8011 Dem Tab. I V .
ftfnei' uni) ïiefc^ prodna mit feiner Ciinge multiplicivet, fo finDet nianroic oicl ma^I
ein fo((t)eS 9)îaa§ (un folive) in Dem Sti'icf entWteii.
Exempli gratia.
Toifes gilg 30»
Câline 2 - 6 '
«rfitc -- -- -61J3 6 Quadrat-Son.
6 Bcnj&D^
6 -- Sii-cite
36 Qiiadrat-3on SliitÇe.
144 Soll cî)cr 2 Toifes.
36
S64
432
5r84 Cubic.3oI[.
Siefe 5184 Cubic-3o((in3î^ciIaetWet tf)ut 1728 tveltf)««ein Cubic-Sug ifl.
I 2 3oa,
12 3ctt.
2 4
12
144
12
288
144
1728 Cubic-3i)a.
S(?a«n ein etücf 2 Toifes fang, 6 30a 6rcit unö 5ort; inS ©eDiCl•^te/ fo i(l tiefet
3nn&ait ein folt^e^ Süaag (im folive) efter 3 Cubifitte gnfie, c5er 5184 Cubifc^e Solle-
' §• 81.
SKan fan aud) ein ©tncf §ol6 alfo aiiSnicffen, iiitieni man feinen Jn^dlt nacS Cubic
5wff«n Met, mit) 6ic ©umma oon biefen mit 3 dividiret, &er Quotient gicbt 6ie Sujt
ter Sdliven fo gefutfet »oröen. 3um Exempel:
SKan roiU iDiffen JiaS £0ina6 Stntf §olgcS fteffen ®rö(Te oben angegeben, fo multiplicivet
man 12 Jug 06er 2 Toifes mit 6 Soll. SaS Produa giebt 6 Quadratgu
§, »elcIjeS noc6 mit 6 antern Sollen ju multiplicircn, fo gieOt Siefen neue Produft
3 Cubic-gu§.
SKan ftatnct^ eine anDere S(rt5 taSJ^ole 5u meffen, begmegen t^eilet nianfta^ Sianf
(un folive) in 144 f'eine ©tiitfen, Seren jeiieS 3 Su§ lang unb i 30II lang unD breit,
folgent)^ Jdit ein folc{)cff ©tnefgen 36 Cubic-3oll. ftube aber btefe 21rt& nict)t fo gc?
filjicft aK bic erfle, beren mi(6 allemal;l in meinem Caiculo gefc^roint» jit cxpediren, bes
bienet. Mr. de la Hire gibt eine Tabelle 5u biefen Caiculo.
60 man mehrere ©tücfen §olg oon unterfcftiebener Sange unb »on einerlei) ©icfe
^at, wie eS gewiffe ®aMen giebt le. fo fummiret man fie jufammeii, eine tange jn befom<
men, unb mattet baS übrige iBie f(I)on geroicicn.
Sie q3fäl)le muffen auf eine anberc Slrtl> auSgemelTen rcerben aK ba^ bcfc|lageiic
J^ot^, roeil fle nic^t an bet;ben £nben oon einerlei; Sitfe, unb orbentlic^ runb fiiib. JKait
mifiet alfo ein jebeSStütf in feinet SDJitte apart, uiib äioar mit einer ©t&nur fo man
Eiai'um legt, unb ^ernacj on einen in gug unb Soll getjjeilten SÜJaaßilab Ddlt, auf roeWen
itianbie Circumferengbe^ ^pfa^le^ (ober Stamme») finbet, fo man nacl) ben Siegeln
ber
Cap. I X . Sgon im itè Tab. i v . 43
J)er Geometrie quadrirt (ober biefe^ ©rcutó Aream flieget, unb biefe in bie Cänge beS
spfa^tó multipliciret, feinen Cubifc^en 3n&alt ju befcmmen). ©iefe gefunbenen SOiaafle
fan man in eine Xabelle ju einen jeben «PfaW fo numerirt rcerben, ft^reiben nat!) fo'äen»
Jen ModelL
§. 82.
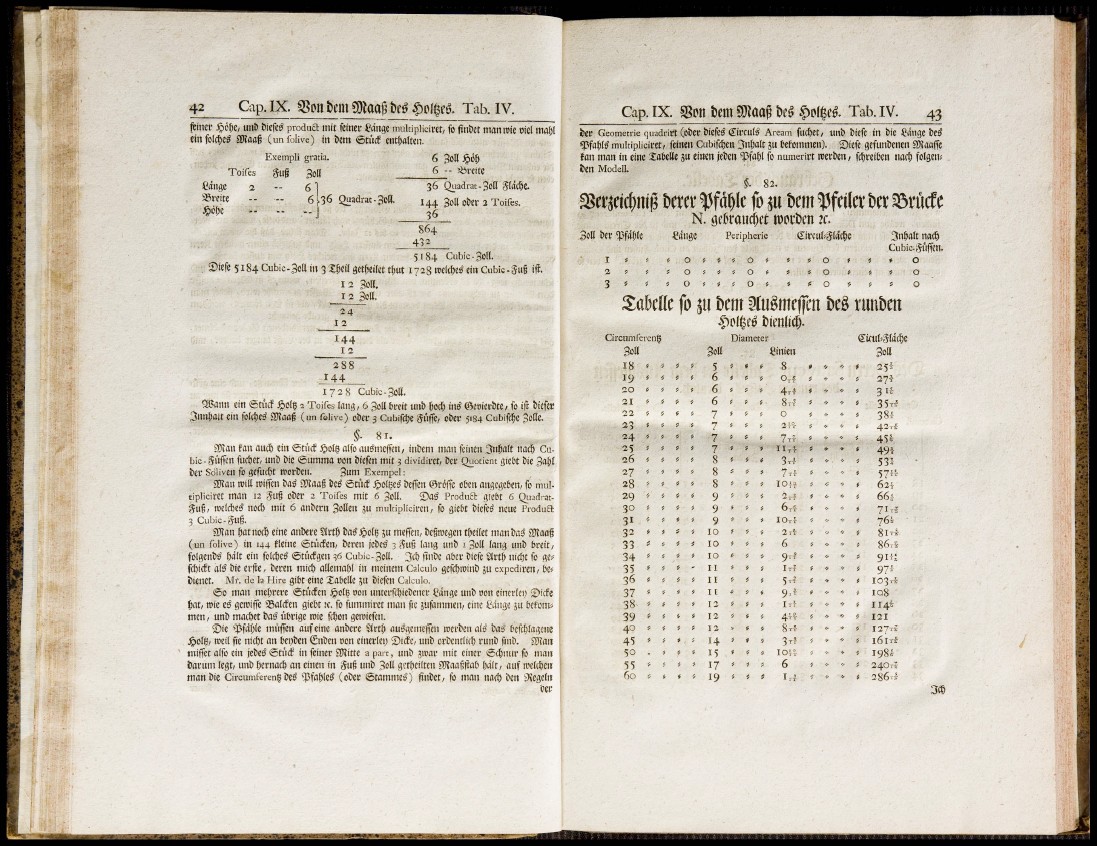
SSetjdc^ni^ Um ^ f a ^ l e fo j u t»em ^ f e i l e t Ux ^ r u c f e
N . geßraucf)e(: tpocbcn jr.
Cänge Peripherie dircutSMc^c 3n^alt nac6
Cubic-gnffen.
Ï 50 f 'f * O
f O f f f O f i f O i 5 5 O
ä O f J s O s S f O 5 5 t O
Sott ber qjfdf^le
Sa^eKe fo j u bem 5fuême||cn M ruuDcn
Dienlich.
CirciimPerenÇ Diameter eiful<31â(|e
Soll SoU Cinieii Sofl
18 5 < ' » 5 5 « « 8 * » 25i
19 5 « 5 s 6 < 5 > s 5 27Î
20 f < > « 6 » 5 » 4rï ( » 3 li
21 > » > » 6 < > > 8t? 5 " » 35Ti
22 '/ î . ^ 7 l i ' , 0 f " -- 38i
23 > 5 ; < 7 > j j 2» f " e 42rf
24 » < ' ^ 7 > < 7tï f " 45i
25 > < < < 7 = ï . II,} ö • > 49t
26 » < » 8
» 8
^ . . 3rf 6 " " 53i
27 ' ^
» » > 7X1 i " > 57»
28 '' î 5 8 > > < lOfï 5 - > 62f
29 » ' ' 9 5 ? - « 66t
30 » « ' 9 < » ä i " » 7ixï
31 « » . 9 f ä > IOTÏ 5 . 76i
32 • . Ü '/ 10 ' f 2T'C - » 8IT1
33 s . ä 5 10 > 1 6 Î " > 8Sii
34 « » 10 0 . 9„' i " s 9 Hl
35 ' » > - II < i 1 I-rf i - . 97i
36 . . ! J II ' i > 5tÏ - » 103rl
37 ' > < Il . , 9,1 t " < IQ8
38 » '' » 12 » < > iTt f > 1144
39 ' > ^ « 12 > < . 4VÏ 5 " » 121
40 = < s f 12 . > > 8t? ï • s I27TÎ
45 ' » . < 14 » < 3T? 'f - 5 lÖiTi
50 . . î 15 « 5 « lOK- - > i98i
55 ' < < 17 i >> 6 f " ' 240TÎ
60 . . 5 19 » « Iii Î - » 2S6ri m